Поляризация света. Естественный и поляризованный свет.

Следствием теории Максвелла является поперечность световых волн: напряженность электрического поля E, вектор индукции магнитного поля B и скорость распространения волны v образуют правую тройку векторов. Действие света на вещество определяется в основном колебаниями вектора напряженности. В соответствии с этим вектор напряженности называют еще световым вектором.

Рассмотрим два взаимно перпендикулярные электрические колебания (вдоль осей x и y), отличающиеся по фазе на d

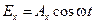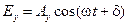, . (17-19)

Результирующая напряженность E является их векторной суммой. Угол j между вектором E и осью x определяется выражением

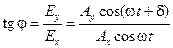. (17-20)

Естественный свет. Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Если разность фаз d претерпевает случайные хаотические изменения, то и угол j, т.е. направление светового вектора E, будет испытывать скачкообразные изменения. На этом основании естественный свет можно представить как наложение двух некогерентных световых волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность.

Плоско поляризованный свет. Допустим, что разность фаз d постоянна и равна нулю или p (когерентные волны). Тогда согласно (17-20)

.
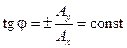Следовательно, результирующее колебание совершается в фиксированном направлении. – волна оказывается плоско поляризованной.

Круговая и эллиптическая поляризация света. Допустим теперь, что 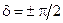. С учетом 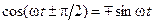с помощью уравнения (17-19) можно получить

.

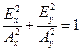Следовательно, световой вектор в некоторой точке описывает при прохождении волны эллипс, оси которого ориентированы вдоль x и y. Такая волна называется эллиптически поляризованной. При произвольном постоянном d в общем случае получается эллиптическая поляризация, причем оси эллипса не совпадают с осями координат.

При разности фаз равной нулю или p, эллипс вырождается в прямую и получается плоско поляризованный свет. При 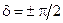и равенстве амплитуд складываемых волн эллипс вырождается в окружность – получается циркулярно поляризованный (поляризованный по кругу) свет.

В зависимости от направления вращения вектора E различают правую и левую эллиптическую и круговую поляризацию. Будем наблюдать за вращением вектора E со стороны, в которую движется волна. Если его вращение происходит по часовой стрелке, поляризация называется правой, в противном случае – левой.

Плоскость, в которой лежит световой вектор в плоско поляризованной волне, называется плоскостью колебаний. По историческим причинам плоскостью поляризации называется плоскость, перпендикулярная в плоскости колебаний, т.е. плоскость в которой лежит вектор B.

Плоско поляризованный свет можно получить из естественного с помощью приборов, называемых поляризаторами. Поляризаторы свободно пропускают колебания, параллельные некоторой плоскости (плоскости поляризатора), и полностью или частично задерживают колебания перпендикулярные этой плоскости. На выходе из поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями другого. Такой свет называется частично поляризованным. Частично поляризованный свет, как и естественный, можно представить в виде наложения двух некогерентных плоско поляризованных волн с взаимно перпендикулярными плоскостями колебаний. В случае естественного света интенсивность этих волн одинакова, а в случае частично поляризованного – разная.

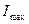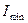Если пропустить частично поляризованный свет через идеальный поляризатор, то при его вращении вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от до . Выражение

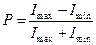(17-21)

называется степенью поляризации. Для плоско поляризованного света 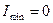и 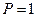; для естественного света 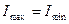и 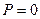. К эллиптически и циркулярно поляризованному свету, колебания которых полностью упорядочены, понятие степени поляризации не применимо, поскольку формальное применение (17-21) дает .

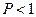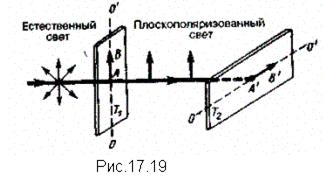
Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления (например, пропускающие колебания, параллельные главной плоскости поляризатора, и полностью задерживающие колебания, перпендикулярные этой плоскости). В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например кристаллы. Из природных кристаллов, давно используемых в качестве поляризатора, следует отметить турмалин.

Рассмотрим классические опыты с турмалином (рис.17.19).

Направим естественный свет перпендикулярно пластинке турмалина Т₁,вырезанной параллельно так называемой оптической оси ОО'. Вращая кристалл Т₁ вокруг направления луча, никаких изменении интенсивности прошедшего через турмалин света не наблюдаем. Если на пути луча поставить вторую пластинку турмалина Т₂и вращать ее вокруг направления луча, то интенсивность света, прошедшего через пластинки, меняется в зависимости от угла а между оптическими осями кристаллов по закону Малюса*:

.

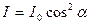где I₀ и I - соответственно интенсивности света, падающего на второй кристалл и вышедшего из него. Следовательно, интенсивность прошедшего через пластинки света изменяется от минимума (полное гашение света) при a = p/2 (оптические оси пластинок перпендикулярны) до максимума при a = 0 (оптические оси пластинок параллельны). Однако, как это следует из рис. 17.20, амплитуда Е световых колебаний, прошедших через пластинку T₂ будет меньше амплитуды световых колебаний E₀, падающих на пластиду Т₁.

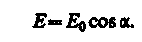
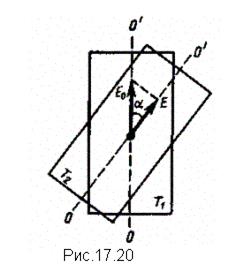
Если пропустить естественный свет через два поляризатора, главные плоскости которых образуют угол 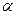, то из первого выйдет плоскополяризованный свет, интенсивность которого I₀ = 1/2I_ест из второго выйдет свет интенсивностью I = I₀cos²a. Следовательно, интенсивность света, прошедшего через два поляризатора,

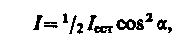
откуда I_max = 1/2 I_ест (поляризаторы параллельны) и I_min = 0 (поляризаторы скрещены).