Классификация задач принятия решений
В настоящее время не существует общепринятой универсальной классификационной схемы задач принятия решений (ЗПР). Однако можно выделить отдельные классификационные признаки, а именно:
1. Количество целей операции, преследуемых одной стороной, и соответствующих целям критериев оптимальности.
2. Наличие или отсутствие зависимости критерия оптимальности и дисциплинирующих условий от времени.
3. Наличие случайных и неопределенных факторов, влияющих на исход операции. Этот признак назван признаком «определенность - риск - неопределенность».
По признаку количества целей различают одноцелевые и многоцелевые задачи принятия решений. Реальные управленческие решения, как правило, являются многоцелевыми. В этих задачах возникает проблема согласования противоречивых целей при выборе решений. Если цели описаны формализованно, в виде целевых функций, то одноцелевые задачи называют однокритериальными (или скалярными), а многоцелевые - многокритериальными (или векторными) задачами принятия решений.
По второму классификационному признаку ЗПР делятся на два больших класса: статические и динамические ЗПР. В статических ЗПР критериальная функция и дисциплинирующие условия не зависят от времени. Динамические задачи сложнее статических и еще не получили широкого применения в экономических исследованиях.
По третьему классификационному признаку - «определенность - риск - неопределенность» - задачи принятия решений делятся на три больших класса:
1. Принятие решений при определенности, или, иначе, детерминированные ЗПР. Они характеризуются однозначной, детерминированной связью между принятым решением и его исходом. Это наиболее простой и изученный способ принятия решений, когда относительно каждой стратегии оперирующей стороны заранее, до проведения операции, известно, что она неизменно приводит к некоторому конкретному результату. В детерминированных ЗПР критерий оптимальности и ограничения зависят только от стратегий оперирующей стороны и фиксированных детерминированных неконтролируемых факторов, т.е. факторов, полностью известных оперирующей стороне.
2. Принятие решений при риске, или, иначе, стохастические ЗПР. В этом случае каждая стратегия оперирующей стороны может привести к одному из множества возможных исходов, причем каждый исход имеет определенную вероятность появления. Предполагается, что принимающему решение лицу эти вероятности заранее, до проведения операции полностью известны. Однако, несмотря на то что все случайные явления и процессы, сопровождающие операцию и влияющие на ее исход, хорошо изучены и их статистические характеристики известны, исход каждой конкретной реализации операции заранее (до ее проведения) неизвестен, случаен. В этом смысле оперирующая сторона всегда рискует (в большей или меньшей степени) получить не тот результат, на который она ориентируется, выбирая свою оптимальную стратегию в расчете на осредненные, статистические характеристики случайных факторов.
3. Принятие решений в условиях неопределенности. В данных ЗПР критерии оптимальности зависит кроме стратегии оперирующей стороны и фиксированных факторов также от неопределенных факторов, не подвластных оперирующей стороне и не известных ей в момент принятия решения.
Классификация задач принятия решений представлена на рис. 5.1.2. С точки зрения наличия исходных данных определенность и неопределенность представляют два крайних случая, а риск определяет промежуточную ситуацию.







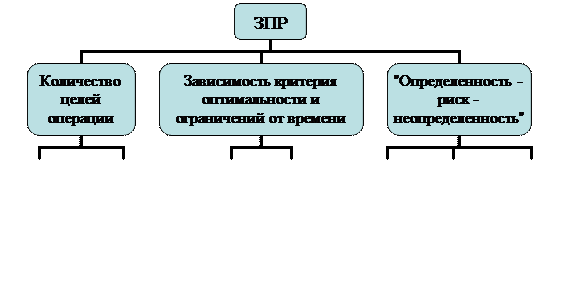

Рис. 5.1.2. Классификационное «дерево» ЗПР
Степень неинформированности о данных непосредственно определяет, каким образом задача формализуется и решается. Очевидно, неполнота данных усложняет задачу принятия решений и неизбежно приводит к менее удовлетворительным результатам. Принятие решений в условиях определенности производится при наличии полной и достоверной информации о проблемной ситуации, целях, ограничениях и последствиях решений. Цели и ограничения формально определяются в виде целевых функций и неравенств (равенств).
Критерий выбора определяется минимумом или максимумом целевой функции. Наличие такой информации позволяет построить формальную математическую модель задачи принятия решений и алгоритмически найти оптимальное решение. Для решения ЗПР в условиях определенности применяются различные методы оптимизации, например, методы математического программирования: линейного, нелинейного, динамического.
В настоящее время сформулированы типовые задачи, в основном производственно-экономического характера, для которых разработаны алгоритмы принятия оптимальных решений, основанные на методах математического программирования. К числу таких задач, например, относятся задачи размещения ресурсов, назначения работ, управления запасами, транспортные задачи и т.п. Роль человека в решении задач данного класса состоит в приведении реальной ситуации к типовой задаче математического программирования и в утверждении получаемого формально оптимального решения. Излагаемый в данной главе материал не относится к решению задач данного класса.
В условиях недостаточности данных часто используются противоречащие друг другу подходы к задачам принятия решений и оценке их результатов. При полной определенности критерий максимума прибыли (или минимума затрат) является почти универсальным. Напротив, для ситуаций с риском или неопределенностью существует ряд возможных критериев. Например, в условиях риска иногда целесообразна максимизация ожидаемой прибыли, но встречаются случаи, когда это неверно. Другие критерии образуют целый спектр от максимально «пессимистичных» до максимально «оптимистичных». И еще более положение усложняется в условиях неопределенности.
Задачи принятия решений в условиях неопределенности непосредственно связаны с управленческими решениями. Для этих задач характерна большая неполнота и недостоверность информации, многообразие и сложность влияния социальных, экономических, политических и технических факторов. Эти обстоятельства не позволяют, по крайней мере, в настоящее время, построить адекватные математические модели решения задач по определению оптимального решения.
На рис. 5.1.3 указаны методы решения ЗПР различных классов.
В большинстве задач принятия решений требуется выбирать наилучший способ (или способы) действия из некоторого множества допустимых альтернатив. В этих же задачах предполагается, что сама система не стремится «помешать» лицу, принимающему решение. Такая ситуация характеризуется отсутствием недоброжелательного противника лицу, принимающему решение.
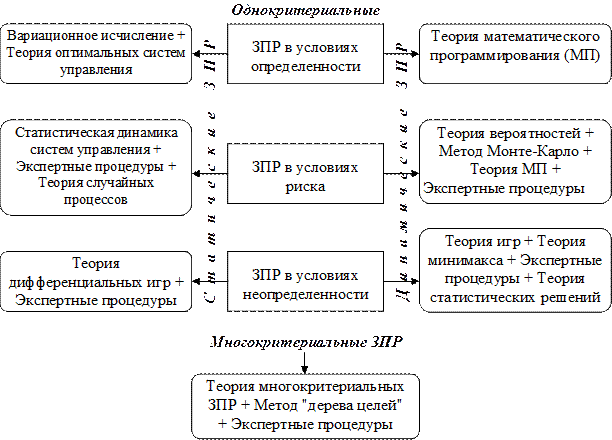
Рис.5.1.3 Математический аппарат решения ЗПР
В процессах принятия решений при наличии неопределенности существуют ситуации конкуренции, когда два (или более) участника находятся в конфликте, и каждый стремится как можно больше выиграть у другого (других). Эти ситуации отличаются от обычных процессов принятия решений в условиях неопределенности тем, что принимающему решение противостоит мыслящий противник. Теория, в которой рассматриваются подобные задачи принятия решений, известна как теория игр.
Большая совокупность неструктурируемых задач представляет при этом значительный интерес для различных областей человеческой деятельности. Невозможность выработки стандартной процедуры их решения повлекла необходимость создания программных средств, предназначенных для решения поставленных задач посредством использования обобщенных баз данных и известных методик их алгоритмической обработки. Соответствующая методология представляет собой новую информационную технологию, обеспечивающую системы поддержки и принятия решений и т.н. экспертные системы (СППР, ЭС).
СППР и ЭС основаны на использовании знаний экспертов (опытных специалистов в какой-либо предметной области). ЭС относятся к интеллектуальным вычислительным системам, реализующим на практике идеи и методы искусственного интеллекта. При этом имитируется поведение эксперта при решении конкретной поставленной задачи на основании его знаний и опыта. Это позволяет оказать помощь специалистам при затруднениях в решении возникающих проблем.
Другой тип компьютерных систем новой информационной технологии - СППР - предназначен для оказания помощи лицам, ответственным за принятие решения на различных уровнях, в неструктурируемых или слабо структурируемых ситуациях выбора. Такие системы не заменяют систему предпочтений данного лица, а лишь расширяют его способности при невозможности полностью переложить решение задачи на ЭВМ ввиду необходимости учета субъективного мнения. Таким образом, СППР представляют собой человеко-машинную информационную систему, предназначенную для решения задач в ситуации выбора альтернатив при нежелательности полного автоматического представления проблемы.
Основой СППР являются: база данных, средства общения с пользователем (интерфейс) и широкий набор методов и моделей математического программирования, статистического анализа, теории игр, теории принятия решений, а также эвристических методов, обеспечивающих адаптивность системы и обучение.
Широкое приложение СППР имеют в областях планирования и прогнозирования для различных видов управленческой деятельности.
Существенное различие между ЭС и СППР при возможной внешней похожести состоит в их целевой направленности. СППР призваны помочь человеку в решении стоящей перед ним задачи, а ЭС - заменить человека при решении проблемы. Сходство ЭС и СППР демонстрируется в наличии некоторых интеллектуальных черт в ССПР, если в их структуру включить базу знаний и использовать механизм логического вывода. В таком случае СППР способна работать в условиях неполноты информации, использовать вероятностные выводы, вырабатывать суждения и объяснения, которые выдаются в качестве советов.
Перспектива развития двух типов информационных программных систем - ЭС и СППР - связана с их сближением и возможностью создания систем, позволяющих использовать различные типы знаний в решении тех или иных задач, выработать единый подход, характерный для исследования в области принятия решений, оптимального управления, извлечения и представления знаний, компьютерной логики, языкового общения.
Дата добавления: 2015-01-13; просмотров: 2067;
