РАЗРАБОТКА СЛОЖНЫХ ПРОГРАММНЫХ СИСТЕМ
Рассмотрим временную диаграмму работы системы массового обслуживания (рис. 1), отразив на ней последовательность поступления требований, помещение требований в очередь и обработки серверами системы.
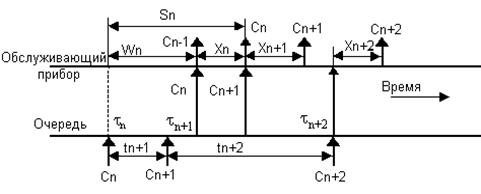
Рис. 1. Временная диаграмма работы системы массового обслуживания.
С увеличением числа требований растет время ожидания. Установим соотношение между средним числом требований в системе, интенсивностью потока и среднего времени пребывания в системе. Обозначим число поступающих в промежутке времени (0 , t) требований как функцию времени α(t).
Число исходящих из системы заявок (обслуженных) на этом интервале обозначим δ(t). На рисунке 2 показаны примеры функциональных зависимостей этих двух случайных процессов от времени.
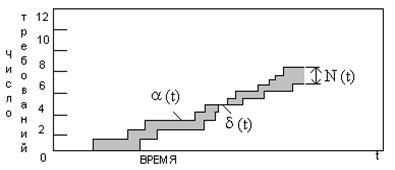
Рис. 2 Зависимость между средним числом требований в системе, интенсивностью потока и средним времени пребывания в системе.
Число требований, находящихся в системе в момент t будет равно:
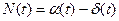 .
.
Площадь между двумя рассматриваемыми кривыми от 0 до t - дает общее время, проведенное всеми заявками в системе за время t.
Обозначим эту накопленную величину γ(t) . Если интенсивность входного потока равна λ, а средняя интенсивность за время t: 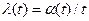 ,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно:
,то время, проведенное одной заявкой в системе, усредненное по всем заявкам будет равно:
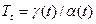 .
.
Наконец, определим среднее число требований в системе в промежутке (0,t):
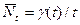 .
.
Из последних трех уравнений следует, что: 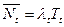 , (где
, (где 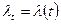 ).
).
Если в СМО существует стационарный режим, то при t→ ∞ , будут иметь место соотношения:
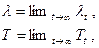
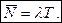
Последнее соотношение означает, что среднее число заявок в системе равно произведению интенсивности поступления требований в систему на среднее время пребывания в системе. При этом не накладывается никаких ограничений на распределения входного потока и времени обслуживания. Впервые доказательство этого факта дал Дж.Литтл и это соотношение носит название формула Литтла.
Интересно, что в качестве СМО можно рассмотреть только очередь из заявок в буфере. Тогда формула Литтла приобретает иной смысл - средняя длина очереди равна произведению интенсивности входного потока заявок на среднее время ожидания в очереди: 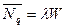 .
.
Если наоборот рассматривать СМО только как серверы, то формула Литтла дает:
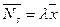 ,
,
где 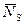 – среднее число заявок в серверах, а
– среднее число заявок в серверах, а 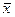 – среднее время обработки в сервере.
– среднее время обработки в сервере.
В любом случае: 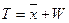 .
.
Одним из основных параметров, которые используются при описании СМО, является коэффициент использования (utilization factor). Это фундаментальный параметр, так как он определяется как отношение интенсивности входного потока к пропускной способности системы. Поскольку пропускная способность СМО содержащей m серверов может быть определена как: 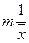 , то коэффициент использования может быть определен как:
, то коэффициент использования может быть определен как:
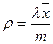 .
.
Нетрудно видеть, что коэффициент использования равен в точности интенсивности нагрузки, если СМО с одним сервером и в m раз меньше для систем с m серверами. Величина коэффициента использования равна среднему значению от доли занятых серверов и 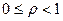 .
.
Если в СМО типа G/G/1 существует стационарный режим и можно определить вероятность того, что в некоторый случайный момент сервер будет свободный, то
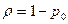 .
.
СРС 3 по дисциплине “Теория распределение информации»
Наименование темы: Стационарные вероятности рк для СМО типа М/М/1.
На рис. 1 приведен график вероятностей того, что в очереди находится k заявок в установившемся режиме.
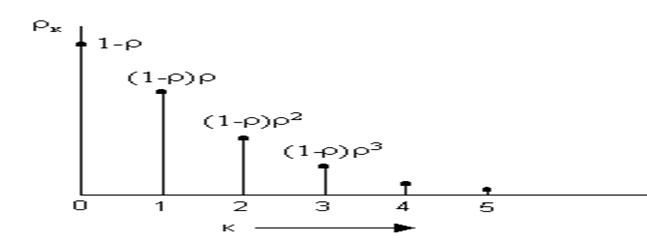
Рис. 1 Стационарные вероятности рк для СМО типа М/М/1.
Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:
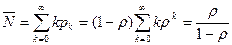 .
.
График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 2.
Найдем теперь дисперсию длины очереди: 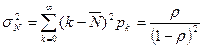 .
.
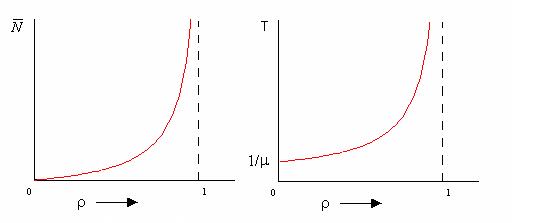
Рисунок 2 Среднее число требований Рисунок 3 Среднее время пребывания
в системе типа М/М/1 требования в системе типа М/М/1 как функция ⍴
Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.
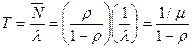 .
.
На рис. 3 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки).
При увеличении коэффициента использования, длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρ к единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО.
Наконец найдем вероятность того, что в очереди будет находиться не менее чем k заявок и того, что в очереди менее k заявок.

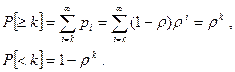
Итак, в ходе анализа простейшей системы М/М/1 удалось в аналитическом виде найти все практически интересные характеристики QoS системы.
СРС 4 по дисциплине “Теория распределение информации»
Наименование темы: Cистема с конечным накопителем: M/M/1:N
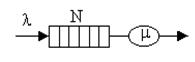 Рассмотрим СМО, для которой фиксировано максимальное число ожидающих заявок. Предположим, что в системе может находиться N заявок, включая находящуюся на обслуживании в сервере. Любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему. В телефонии такие вызовы называют потерянными. Поступающие заявки образуют Пуассоновский поток, а обслуживание осуществляется одним сервером с показательным законом распределения времени обработки. Приспособим для описания такой системы модель процесса гибели-размножения.
Рассмотрим СМО, для которой фиксировано максимальное число ожидающих заявок. Предположим, что в системе может находиться N заявок, включая находящуюся на обслуживании в сервере. Любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему. В телефонии такие вызовы называют потерянными. Поступающие заявки образуют Пуассоновский поток, а обслуживание осуществляется одним сервером с показательным законом распределения времени обработки. Приспособим для описания такой системы модель процесса гибели-размножения.
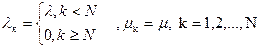
Эта система эргодична и диаграмма интенсивностей переходов может быть изображена так как на рис. 1.
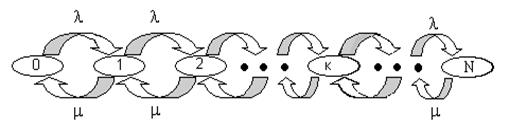
Рис. 1 Диаграмма интенсивностей переходов системы типа М/М/1:N.
Найдем распределение вероятностей в стационарном режиме непосредственно из общей формулы
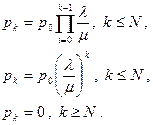
Найдем теперь начальную вероятность, следуя общей формуле:
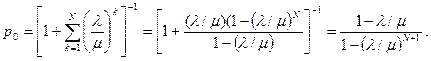
Таким образом, окончательная формула для стационарных вероятностей будет:
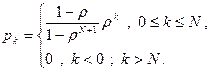
Проанализируем характеристики качества обслуживания (QoS) для такой системы. Важнейшей характеристикой будет являться вероятность блокировки – потери заявки. Очевидно, что это произойдет с вероятностью переполнения буфера, поэтому для расчета вероятности блокировки можно использовать формулу:
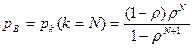 .
.
Например, для системы с коэффициентом использования 0.5 при размере буфера N=18 вероятность блокировки будет больше 10-6, а при размере N=19, меньше этого значения. Следовательно, для получения вероятности блокировки такой величины необходимо предусмотреть размер буфера не менее 19.
Средняя длина очереди в буфере может быть найдена как:
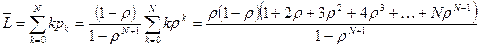 .
.
Соответственно задержка может быть найдена на основе формулы Литтла
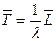 .
.
Определим пропускную способность системы как число заявок, обслуживаемых системой в одну секунду. Очевидно, что при вероятности блокировки PB пропускная способность может быть найдена как чистая интенсивность поступлений, то есть:
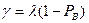 .
.
С точки зрения выхода системы пропускная способность может быть определена иначе. Если система всегда была бы непуста, то ее производительность равнялась бы величине обратной среднему времени обслуживания, то есть μ. Однако, поскольку часть времени система может простаивать, вероятность того, что в ней нет ни одной заявки отлична от нуля, реальная производительность может быть выражена как:
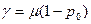 .
.
Подставив выражения для вероятности простоя сервера для системы с бесконечным размером буфера, получим:
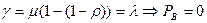 .
.
Для системы с конечным буфером получаем:
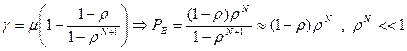 .
.
В качестве реального примера рассмотрим концентратор сети с коммутацией пакетов, который обрабатывает пакеты со средней длиной 1200 бит. При скорости передачи в канале 2400 бит/с средняя пропускная способность его составит μ=2 пакета/с. Если полный входной поток имеет интенсивность λ =1 пакет/с, то ρ =0.5 и можно рассчитать, что при размере буфера N =9 пакетов в среднем по 1200 бит, вероятность блокировки составит 0.001. Для того, чтобы получить вероятность блокировки 0.000 001 нужно предусмотреть буфер длиной не менее 19 пакетов по 1200 бит, т.е. около 2850 байт.
СРС 5 по дисциплине “Теория распределение информации»
Наименование темы: Система обслуживания M/M/m:K/M конечное число источников нагрузки, m серверов и конечный накопитель
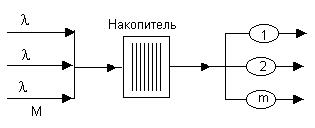 Основной смысл изучения такой системы состоит в том, что входной поток в такой системе может рассматриваться как примитивный, то есть параметр потока зависит от числа требований, находящихся на обслуживании. Эта зависимость определяется таким образом, что из M источников пуассоновского потока с постоянным параметром λ получают отказ те требования, которые поступают в систему тогда, когда в ней уже имеются K заявок. Система описывается процессом типа гибели-размножения с диаграммой интенсивностей переходов на рис. 1.
Основной смысл изучения такой системы состоит в том, что входной поток в такой системе может рассматриваться как примитивный, то есть параметр потока зависит от числа требований, находящихся на обслуживании. Эта зависимость определяется таким образом, что из M источников пуассоновского потока с постоянным параметром λ получают отказ те требования, которые поступают в систему тогда, когда в ней уже имеются K заявок. Система описывается процессом типа гибели-размножения с диаграммой интенсивностей переходов на рис. 1.
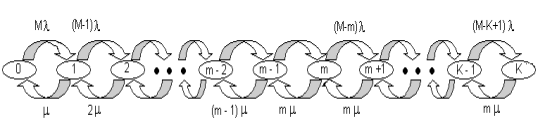
Рис. 1. Диаграммой интенсивностей переходов для СМО типа M/M/m:K/М.
и параметрами интенсивностей:
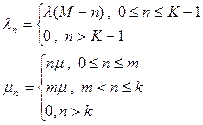
Воспользовавшись формулам для стационарных вероятностей, получим:
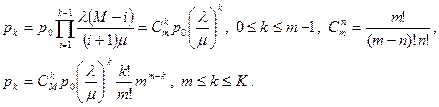
Формула для вероятности простоя очень громоздка и здесь не приводится. Если считать, что K = m , то есть в системе только чистые потери (длина буфера совпадает с числом серверов), то распределение стационарных вероятностей может быть дано в виде так называемого распределения Энгсета:
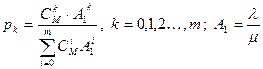
Эта формула имеет следующую интерпретацию.
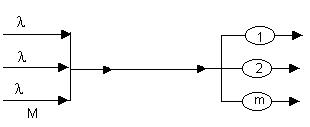 Некоторая система массового обслуживания, имеющая М входных линий, распределяет поступающие с них заявки на m серверов. Интенсивность входного потока зависит от того, сколько серверов занято обслуживанием таким образом, что интенсивность входного потока линейно убывает с числом занятых серверов :
Некоторая система массового обслуживания, имеющая М входных линий, распределяет поступающие с них заявки на m серверов. Интенсивность входного потока зависит от того, сколько серверов занято обслуживанием таким образом, что интенсивность входного потока линейно убывает с числом занятых серверов : 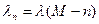 .
.
Максимальная нагрузка, поступающая на один вход, определяется как: 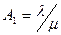 .
.
Вероятность того, что при показательном законе распределения времени обслуживания в стационарном режиме будет занято k серверов, будет определяться как раз вышеприведенной формулой Энгсета. Систему такого типа можно назвать M/M/m:M. Полученное распределение также позволяет рассчитать вероятность того, что будут заняты все серверы. Для этого достаточно положить k = m . Как видно, она отличается от полученной ранее формулы потерь Эрланга. Это распределение также часто встречается на практике и задается функцией Энгсета:
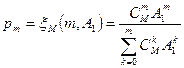 .
.
На практике применима также модель Молина (Molina), которая также называется моделью потерянных вызовов (LCH – Lost Calls Held). Это математическая модель блокировки телефонного трафика, в которой блокированные обращения сохраняются в течение определенного времени задержки, хотя и не обслуживаются. Эта модель подобна модели, описываемой С – формулой Эрланга, с которой иногда и путается. Вероятность блокировки для N линий, создающих интенсивность А имеет вид:
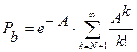 .
.
СРС 6 по дисциплине “Теория распределение информации»
Наименование темы: Анализ систем связи
Рассмотрим узел коммутации каналов. На практике это может быть транзитная АТС, которая коммутирует соединительные линии разных направлений, оконечная АТС, входные линии которой являются как соединительными, так и абонентскими. Это может быть также учрежденческая АТС или выносной концентратор городской станции.
Будем полагать, что коммутатор имеет M входящих и m исходящих линий.
Опишем поток заявок следующими параметрами. Пусть каждый абонент в среднем делает 1 звонок каждые 30 минут, занимая линию в среднем на 3 минуты.
Пусть общее число абонентов М=120. Основной задачей при проектировании является определение числа исходящих линий, достаточного, для обеспечения заданного уровня качества обслуживания. Важнейшей характеристикой качества является вероятность блокировки по времени.
Одним из подходов к анализу является применение модели Эрланга .
Будем рассматривать все вызовы, поступающие от абонентов как общий Пуассоновский поток с параметром: 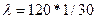 вызовов в минуту.
вызовов в минуту.
Найдем нагрузку: 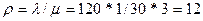 Эрлангов
Эрлангов
Воспользуясь В-формулой Эрланга, можно найти следующие значения вероятностей блокировки при различном числе выходных линий:
| PB,% | m | r/m |
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 1.0 | ||
| 1.7 |
При умеренных нагрузках (5<ρ<50), можно использовать приближенные формулы:
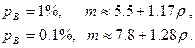 |
Другим подходом является использование модели Энгсета. При этом вероятность блокировки по времени можно рассчитать как значение:
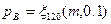 .
.
Найдем несколько значений этой функции.
| pB,% | m | Mρ/m |
| 0.7 | ||
| 0.75 | ||
| 0.86 | ||
| 1.1 | ||
| 1.3 |
Как можно видеть из таблиц, приведенных выше, применение моделей Эрланга и Энгсета несущественно при рассмотрении небольшой удельной нагрузке на сервер, расхождения заметны лишь для больших удельных потенциальных нагрузках. Обычно на практике рассматриваются пучки исходящих каналов и вызовы на каждый из пучков считают Пуассоновскими потоками. К каждому пучку применимо распределение Эрланга. Вероятности состояния каждого из исходящих пучков более приемлемо при этом описывать распределением Энгсета.
СРС 7 по дисциплине “Теория распределение информации»
Наименование темы: Коэффициент использования линии (сервера), единичное приращение интенсивности обслуженной нагрузки
На рис. 1. приведены результаты расчета коэффициента использования линии (сервера):
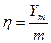 .
.
В предположении ИСС для различных значений g, D=10, pB=0.003.
Характерно, что с ростом числа серверов использование линии сначала увеличивается, а затем уменьшается. В крайних точках m=g и m=gD использование линии одинаково, так как соответствует полнодоступному включению.
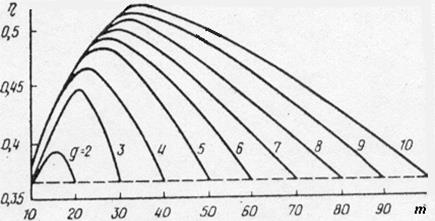
Рис. 1. Среднее использование линии m в НВ в зависимости от емкости пучка m при различных значениях g, D=10 и P=0.003.
Важной практической характеристикой СМО с несколькими серверами является единичное приращение интенсивности обслуженной нагрузки при увеличении числа серверов на единицу и постоянной норме потерь - вероятности блокировки. Эту величину называют единичным приращением
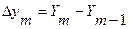 .
.
Для полнодоступных систем при постоянной вероятности блокировки и постоянном числе входных линий из полученных ранее формул для обслуженной нагрузки следуют неравенства:
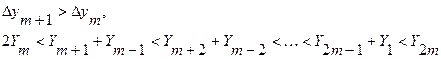
Это неравенство говорит о том, что удвоение числа серверов увеличивает пропускную способность системы более чем вдвое. Рис. 2 показывает зависимость единичного приращения от числа серверов в полнодоступной системе при фиксированной вероятности блокировки. Для неполнодоступных систем рост единичного приращения от числа серверов заметно меньше, чем для полнодоступной.
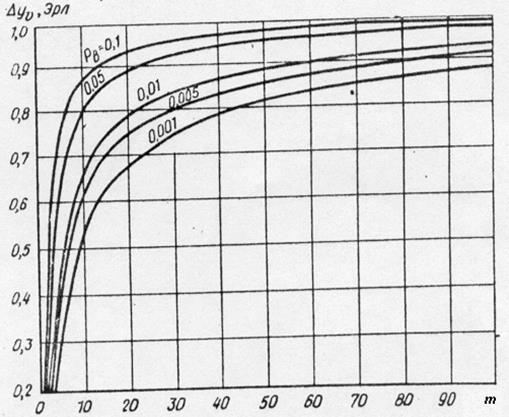
Рис. 2 Зависимость единичного приращения Dyu от числа выходов m при обслуживании простейшего потока и различных вероятностях потерь РВ.
При переходе от схемы ПВ к схеме НВ значение единичного приращения скачкообразно уменьшается.
Эскизные расчеты схем НВ могут проводиться с помощью приближенных формул. Формула О’Делла, позволяющая оценить необходимое число серверов m при неполнодоступной схеме их включения с доступностью D по заданной обслуженной нагрузке Y и вероятности блокировки:
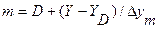 .
.
Здесь используется базовая величина для обслуженной нагрузки D серверами.
Коэффициент использования сервера при γ =1:
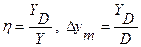 .
.
С ростом γ, величина единичного приращения увеличивается, как было показано, для ИСС можно считать 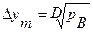 .
.
Пусть на некоторую ИСС поступает γ пуассоновских потоков интенсивностью b=λ/gD каждый. С ростом m число потоков:
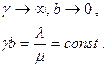
Вероятность занятия одного фиксированного сервера тогда может быть задана величиной в точности равной η=Y/m . Для D фиксированных серверов эта вероятность будет очевидно ηD . Для схем НВ эта вероятность в точности равна pB. Следовательно, приходим к соотношениям
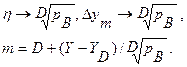
В некоторых странах принято использовать формулу Пальма -Якобеуса для определения обслуженной нагрузки и вероятности блокировки. Она представляет собой систему нелинейных уравнений следующего вида
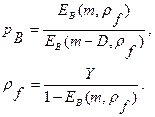
Здесь используется функция Эрланга, определенная ранее.
РАЗРАБОТКА СЛОЖНЫХ ПРОГРАММНЫХ СИСТЕМ
Известно, что основной задачей первых трех десятилетий компьютерной эры являлось развитие аппаратных компьютерных средств. Это было обусловлено высокой стоимостью обработки и хранения данных. В 80-е годы успехи микроэлектроники привели к резкому увеличению производительности компьютера при значительном снижении стоимости.
Основной задачей 90-х годов и начала XXI века стало совершенствование качества компьютерных приложений, возможности которых целиком определяются программным обеспечением (ПО).
Современный персональный компьютер теперь имеет производительность большой ЭВМ 80-х годов. Сняты практически все аппаратные ограничения на решение задач. Оставшиеся ограничения приходятся на долю ПО.
Чрезвычайно актуальными стали следующие проблемы:
q аппаратная сложность опережает наше умение строить ПО, использующее потенциальные возможности аппаратуры;
q наше умение строить новые программы отстает от требований к новым программам;
q нашим возможностям эксплуатировать существующие программы угрожает низкое качество их разработки.
Ключом к решению этих проблем является грамотная организация процесса создания ПО, реализация технологических принципов промышленного конструирования программных систем (ПС).
Настоящий учебник посвящен систематическому изложению принципов, моделей и методов (формирования требований, анализа, синтеза и тестирования), используемых в инженерном цикле разработки сложных программных продуктов.
В основу материала положен двенадцатилетний опыт постановки и преподавания автором соответствующих дисциплин в Рижском авиационном университете и Рижском институте транспорта и связи. Базовый курс «Технология конструирования программного обеспечения» прослушали больше тысячи студентов, работающих теперь в инфраструктуре мировой программной индустрии, в самых разных странах и на самых разных континентах.
Автор стремился к достижению трех целей:
q изложить классические основы, отражающие накопленный мировой опыт программной инженерии;
q показать последние научные и практические достижения, характеризующие динамику развития в области Software Engineering;
q обеспечить комплексный охват наиболее важных вопросов, возникающих в больших программных проектах.
Компьютерные науки вообще и программная инженерия в частности — очень популярные и стремительно развивающиеся области знаний. Обоснование простое: человеческое общество XXI века — информационное общество. Об этом говорят цифры: в ведущих странах занятость населения в информационной сфере составляет 60%, а в сфере материального производства — 40%. Именно поэтому специальности направления «Компьютерные науки и информационные технологии» гарантируют приобретение наиболее престижных, дефицитных и высокооплачиваемых профессий. Так считают во всех развитых странах мира. Ведь не зря утверждают: «Кто владеет информацией — тот владеет миром!»
Поэтому понятно то пристальное внимание, которое уделяет компьютерному образованию мировое сообщество, понятно стремление унифицировать и упорядочить знания, необходимые специалисту этого направления. Одними из результатов такой работы являются международный стандарт по компьютерному образованию Computing Curricula 2001 — Computer Science и международный стандарт по программной инженерии IEEE/ACM Software Engineering Body of Knowledge SWEBOK 2001.
Содержание данного учебника отвечает рекомендациям этих стандартов. Учебник состоит из 17 глав.
Первая глава посвящена организации классических, современных и перспективных процессов разработки ПО.
Вторая глава знакомит с вопросами руководства программными проектами — планированием, оценкой затрат. Вводятся размерно-ориентированные и функционально-ориентированные метрики затрат, обсуждается методика их применения, описывается наиболее популярная модель для оценивания затрат — СОСОМО II. Приводятся примеры предварительной оценки программного проекта и анализа чувствительности проекта к изменению условий разработки.
Третья глава рассматривает классические методы анализа при разработке ПО.
Четвертая глава отведена основам проектирования программных систем. Здесь обсуждаются архитектурные модели ПО, основные проектные характеристики: модульность, информационная закрытость, сложность, связность, сцепление и метрики для их оценки.
Пятая глава описывает классические методы проектирования ПО.
Шестая глава определяет базовые понятия структурного тестирования программного обеспечения (по принципу «белого ящика») и знакомит с наиболее популярными методиками данного вида тестирования: тестированием базового пути, тестированием ветвей и операторов отношений, тестированием потоков данных, тестированием циклов.
Седьмая глава вводит в круг понятий функционального тестирования ПО и описывает конкретные способы тестирования — путем разбиения по эквивалентности, анализа граничных значений, построения диаграмм причин-следствий.
Восьмая глава ориентирована на комплексное изложение содержания процесса тестирования: тестирование модулей, тестирование интеграции модулей в программную систему; тестирование правильности, при котором проверяется соответствие системы требованиям заказчика; системное тестирование, при котором проверяется корректность встраивания ПО в цельную компьютерную систему. Здесь же рассматривается организация отладки ПО (с целью устранения выявленных при тестировании ошибок).
Девятая глава посвящена принципам объектно-ориентированного представления программных систем — особенностям их абстрагирования, инкапсуляции, модульности, построения иерархии. Обсуждаются характеристики основных строительных элементов объектно-ориентированного ПО — объектов и классов, а также отношения между ними.
В десятой главе дается сжатое изложение базовых понятий языка визуального моделирования — UML, рассматривается его современная версия 1.4.
Одиннадцатая глава представляет инструментарий UML для задания статических моделей, описывающих структуру объектно-ориентированных программных систем.
Двенадцатая глава отображает самый многочисленный инструментарий UML — инструментарий для задания динамических моделей, описывающих поведение объектно-ориентированных программных систем. Впрочем, здесь излагаются и смежные вопросы: формирование модели требований к разработке ПО с помощью аппарата Use Case, фиксация комплексных динамических решений с помощью коопераций и паттернов, бизнес-моделирование как средство предпроектного анализа организации-заказчика.
Тринадцатая глава отведена моделям реализации, описывающим формы представления объектно-ориентированных программных систем в физическом мире. Помимо компонентов, узлов и соответствующих диаграмм их обитания здесь приводится пример современной компонентной модели от Microsoft — COM.
В четырнадцатой главе обсуждается метрический аппарат для оценки качества объектно-ориентированных проектных решений: метрики оценки объектно-ориентированной связности, сцепления; широко известные наборы метрик Чидамбера и Кемерера, Фернандо Абреу, Лоренца и Кидда; описывается методика их применения.
Пятнадцатая глава решает задачу презентации унифицированного процесса разработки объектно-ориентированных программных систем, на конкретном примере обучает методике применения этого процесса. Кроме того, здесь рассматриваются методика управления риском разработки, процесс разработки в стиле «экстремальное программирование».
Шестнадцатая глава обучает особенностям объектно-ориентированного тестирования, проведению такого тестирования на уровне визуальных моделей, уровне методов, уровне классов и уровне взаимодействия классов.
Семнадцатая глава демонстрирует возможности применения CASE-системы Rational Rose к решению задач автоматизации формирования требований, анализа, проектирования, компонентной упаковки и программирования программного продукта.
Учебник предназначен для студентов бакалаврского и магистерского уровней компьютерных специальностей, может быть полезен преподавателям, разработчикам промышленного программного обеспечения, менеджерам программных проектов.
Вот и все. Насколько удалась эта работа — судить Вам, уважаемый читатель.
Дата добавления: 2015-03-07; просмотров: 1681;
