Множественные ссылки на порожденные элементы. Пусть исходная сеть соответствует рисунку 12
Пусть исходная сеть соответствует рисунку 12. Тогда ее описание задано в таблицах 68 – 72:
Таблица 68 Таблица 69
| № п/п | Шифр учебной группы | Ссылки (табл.70) | № п/п | Дисциплина | Ссылки (табл.72) | |
| 01-АС | Информатика | 3,4 | ||||
| 01-ИЭ | 1,2,5 | Программирование | 1,2 | |||
| 02-ВТ | Физика |
Таблица 70 Таблица 71 Таблица 72
| № п/п | ФИО студента | Ссылки (табл.72) | № п/п | Оценка | Ссылки (табл.72) | № п/п | Э | ||
| Иванов И.И. | 1,3 | Э1 | |||||||
| Сидоров С.С. | 2,5 | Э2 | |||||||
| Петров П.П. | Э3 | ||||||||
| Федоров Ф.Ф. | Э4 | ||||||||
| Яковлев Я.Я. | Э5 |
Совокупность таблиц 68 и 70 описывает состав учебных групп (рисунок 9), таблица 69 определяет список дисциплин, экзамены по которым сдаются в сессию (рисунок 10), таблица 71 задает состав оценок (т.е. представляет рисунок 11), полученных во время сессии, а таблица 72 определяет только связь между студентами, дисциплинами и полученными на экзаменах оценками.
Рассмотрим решение задач просмотра элементов сети.
Пример 30. Пусть требуется определить, получены ли тройки по Информатике, т.е. qпросмотр = (Оценка =3, Дисциплина= Информатика), где Кдоступ = 3, Информатика. Сеть задана таблицами 68 – 72.
Решение задачи:
1. по таблице 69 определяется элемент с ключом Информатика (задача аналогична поиску по линейному списку по первичному ключу) – это элемент с номером 1;
2. по ссылкам для первого элемента таблицы 69 (поле Ссылки) выбираем порожденные элементы. Они находятся в таблице 72 с номерами 3 и 4. Получаем список {3, 4};
3. по таблице 71 обращаемся последовательно к элементу со значением 3 - это третий элемент. Для него список ссылок из графы Ссылки равен {3};
4. строим пересечение множеств из шагов 2) и 3): {3, 4} ∩ {3} = 3. Поскольку получено непустое множество, формируем утвердительный ответ на поставленный вопрос. Алгоритм заканчивает работу.
Пример 31. Пусть требуется определить, какую оценку по Информатике получил Иванов И.И., т.е. qпросмотр = (ФИО студента =Иванов И.И., Дисциплина =Информатика, Оценка), где Кдоступ = Иванов И.И., Информатика. Сеть задана таблицами 68 – 72.
Решение задачи:
1. по таблице 69 определяется элемент с ключом Информатика – это элемент с номером 1;
2. по ссылкам для первого элемента таблицы 69 (поле Ссылки) выбираем порожденные элементы. Они находятся в таблице 72 с номерами 3 и 4. Получаем список {3, 4};
3. по таблице 70 определяем элемент с ключом Иванов И.И. Его номер – 1;
4. по ссылкам для этого элемента таблицы 70 (поле Ссылки) выбираем порожденные элементы – это элемент 3 из таблицы 72. Получаем список {3};
5. в таблице 71 по полю Ссылки объединяем списки ссылок. Получаем множество {1, 2, 3, 4, 5};
6. строим пересечение всех трех полученных множеств: {3, 4}∩{3}∩{1, 2, 3, 4, 5} = 3. Полученной ссылке соответствует оценка 5 в таблице 71, таким образом, результат решения задачи – пятерка. Алгоритм заканчивает работу.
Пример 32. Пусть требуется определить, какие оценки получены по Информатике, т.е. qпросмотр = (Дисциплина =Информатика, Оценка), где Кдоступ = Информатика. Сеть задана таблицами 68 – 72.
Решение задачи:
1. по таблице 69 определяется элемент с ключом Информатика – это элемент с номером 1;
2. по ссылкам для первого элемента таблицы 69 (поле Ссылки) выбираем порожденные элементы. Они находятся в таблице 72 с номерами 3 и 4. Получаем множество {3, 4};
3. в таблице 71 по полю Ссылки объединяем списки ссылок. Получаем множество {1, 2, 3, 4, 5};
4. строим пересечение полученных множеств: {3, 4}∩{1, 2, 3, 4, 5} = {3, 4}. Полученному списку ссылок соответствуют оценки 5 и 3 в таблице 71, что и является результатом решения задачи. Алгоритм заканчивает работу.
Рассмотрим, как решается задача добавления нового элемента.
Пример 33. Пусть в сеть рисунка 12 требуется поместить элемент со структурой:
| ФИО студента | Шифр учебной группы | Дисциплина | Оценка |
| Петров П.П. | 02-ВТ | Информатика |
т.е. qдобавление = (ФИО студента =Петров П.П., Шифр учебной группы= 02-ВТ, Дисциплина = Информатика, Оценка = 5), где Кдоступ = Петров П.П., 02-ВТ, Информатика, 5.
После размещения элемента в сети она примет вид рисунка 13: новый элемент Э6 показывает связь студента Петрова П.П. с оценкой 5 по информатике (связи выделены жирными стрелками):
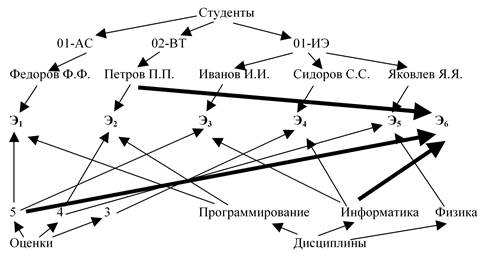
Рисунок 13
Новой сети соответствует описание, помещенное в таблицы 68, 69 (так описан состав учебных групп, список дисциплин, которые не поменялись), а также модифицированные таблицы 70 – 72, представленные в таблицах 73 – 75 (новые и измененные данные показаны заливкой):
Таблица 73 Таблица 74 Таблица 75
| № п/п | ФИО студента | Ссылки (табл.75) | № п/п | Оценка | Ссылки (табл.75) | № п/п | Э | ||
| Иванов И.И. | 1,3,6 | Э1 | |||||||
| Сидоров С.С. | 2,5 | Э2 | |||||||
| Петров П.П. | 2,6 | Э3 | |||||||
| Федоров Ф.Ф. | Э4 | ||||||||
| Яковлев Я.Я. | Э5 | ||||||||
| Э6 |
Дата добавления: 2015-03-03; просмотров: 993;
