А б в г д е ё ж з и й к л м н о п р с т у ф х ц ч ш щ ь ъ ы э ю я
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2
Тогда, например, ключ Сидоров запишется как 8945752 (различие прописных и строчных букв игнорируется). Очевидно, такая замена может привести к тому, что разные нечисловые значения будут иметь одинаковые числовые замены. Это одна из причин потери информации при выполнении алгоритмов рандомизации;
2. порядок числового значения ключа приводится к порядку максимального номера бакета. Например, если максимальный номер бакета - четырехзначное число, то числовой ключ 8945752, полученный в предыдущем шаге, должен быть преобразован в четырехзначное число. Для такого преобразования существуют разные способы. Некоторые из них показаны ниже (в предположении, что максимальный номер бакета – четырехзначное число):
· метод квадратов: значение ключа возводится в квадрат. В полученном числе выбирается средняя часть, состоящая из требуемого количества цифр. Например, для числа 8945752 такое преобразование будет иметь вид:
| ⇒ | ⇒ | |||
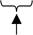
| ||||
| средняя часть числа, состоящая из 4 цифр |
· сдвиг разрядов: разряды ключа делятся на старшие и младшие и "сдвигаются" друг к другу так, чтобы число перекрывающихся разрядов соответствовало требуемому числу цифр. Совмещенные цифры складываются. Например, для числа 8945752 такое преобразование будет иметь вид:
| ⇒ | ⇒ | (13)(16)92 | ⇒ | |||
| ⇓ | совмещенные разряды | результат сложения совмещенных разрядов | окончательный результат | |||
| старшие разряды | младшие разряды |
· метод складывания: ключ делится на 3 части, средняя из которых по количеству цифр равна требуемому порядку. Первая и третья части налагаются на среднюю часть и совмещенные цифры складываются. Например, для числа 8945752 такое преобразование будет иметь вид (здесь средняя часть - 9457):
| ⇒ | 8 25 | ⇒ | (17)47(12) | ⇒ | ||
| ⇓ | наложенные части числа | результат сложения | окончательный результат | |||
| средняя часть числа |
Очевидно, рассмотренные методы могут дать одинаковые результаты для разных числовых значений ключа. Это вторая причина потери информации при рандомизации. Выбор того или иного метода из трех рассмотренных выполняется экспериментально: лучшим считается тот метод, при использовании которого бакеты заполняются элементами относительно равномерно;
3) полученное на предыдущем шаге число умножается на константу С, которая рассчитывается как отношение максимального номера бакета Nmax к максимальному n-разрядному числу, где n – порядок максимального номера бакета. Это позволяет сформировать реальные номера бакетов. Например, пусть максимальный номер бакета – 7000 (это Nmax). Очевидно, n = 4. Тогда упомянутая константа С имеет значение:
С = 7000/9999 = 0,7.
Рассчитаем реальный номер бакета для результата предыдущего шага, полученного методом складывания: 8473 * 0,7 = 5931.
Пример 9. Рассмотрим решение задачи добавления элементов линейного списка таблицы 11.
Поскольку в линейном списке только 4 элемента, пусть максимальный номер бакета Nmax равен 0009, тогда порядок максимального номера бакета n = 4.
Применим алгоритм рандомизации для получения номеров бакетов первичных ключей элементов таблицы 11 – фамилий Скворцов, Соколов, Строков, Супруненко. При этом используем все три метода приведения числового значения ключа к порядку максимального номера бакета.
Решение задачи состоит из следующих шагов:
1. преобразование нечисловых значений ключей в числовые (используется соотношение, приведенное ранее):
Дата добавления: 2015-03-03; просмотров: 2310;
