Продовження таблиці 4.1
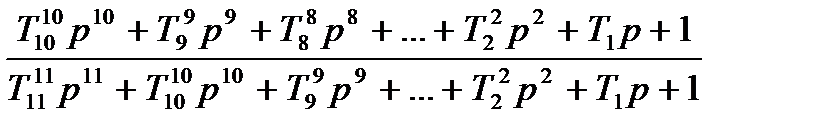
|
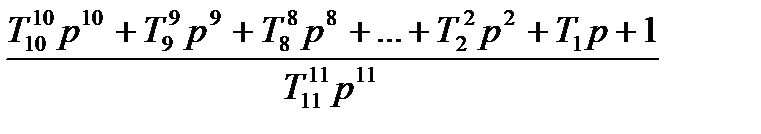
| T11=1/ 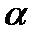 T10=1.188/ T10=1.188/  T9=1.373/ T9=1.373/ 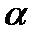 T8=1.571/ T8=1.571/ 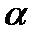 T7=1.793/ T7=1.793/ 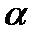 T6=3.053/ T6=3.053/ 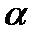 T5=3.370/ T5=3.370/ 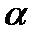 T4=3.777/ T4=3.777/ 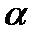 T3=3.333/ T3=3.333/ 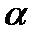 T2=4.165/ T2=4.165/ 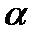 T1=5.609/ T1=5.609/ 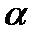
|
Для визначення оптимального закону керування виконана декомпозиція отриманого рішення, шляхом розмикання замкнутої системи автоматичного регулювання, вважаючи уведення негативного одиничного зворотного зв'язку:
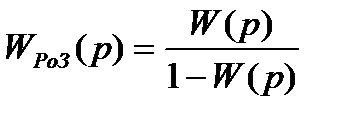 (4.44)
(4.44)
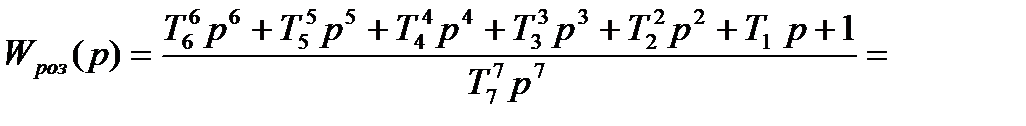
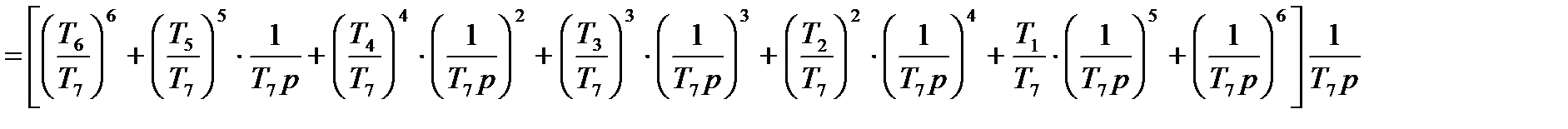 (4.45)
(4.45)
Якщо об'єкт управління представлений у виді інтегруючої ланки, то в цьому випадку багатоканальний регулятор має структуру, яка складається з семи паралельних ланок - пропорційної, інтегральної, двох інтегральних і т. ін. до шести послідовно включених інтеграторів або П І І2 І3 І4 І5 І6. Система характеризується астатизмом шостого порядку, коли відсутні похибки за похідною п'ятого порядку або за другою похідною плавності руху.
Аналіз формул показує, що відношення постійних часу чисельника до постійної знаменника розімкненої електронної системи завжди більше одиниці. Воно поступово зростає досягаючи значення 6,374.
Для випадку коли об¢єкт управління являє собою інтегральну ланку, тоді регулятор можна представити у вигляді паралельного з¢єднання каналів з пропорційною та інтегральними складовими. При збільшенні порядку поліному число таких каналів збільшується пропорційно і кожен складається з послідовного включення інтегральних ланок. Систему керування n-го порядку можна представити такою функціональною схемою, представленою на рис. 3.9.
Представимо систем в просторі змінних стану. Для стаціонарної системи відношенню зображень Лапласа вихідного і вхідного сигналів при нульових початкових умовах:
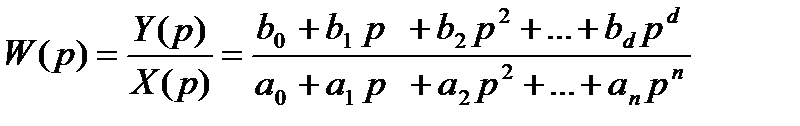 ,
,  (4.46)
(4.46)
відповідає диференціальне рівняння:
any(n)+...+a2y//+ a1ý + a0y = b0x + b1x + b2x// + ...+bdxd (4.47)
Найбільш поширеним способом представлення передатних функцій систем керувань у просторі змінних стану є таке матричне рівняння:
Ý = AY + Bu,
| де | … | ||||
| … | |||||
| А = | … | … | … | … | |
| … | |||||
| - а0/an | - а0/an | ... | an-1/an |
B=[0 0 ... an-1]T; u1=b0x+b1x+b2x// + ...+bdxd (4.48)
Y = [y1, y2 ... yn]T – стовпець змінних стану системи.
Рівнянню (4.48) для передатної функції (4.46) буде відповідати така структура:
 ;
; 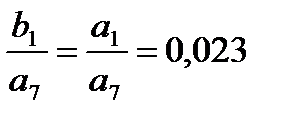 ;
; 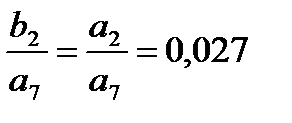 ;
; 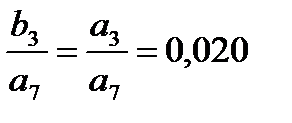 ;
;
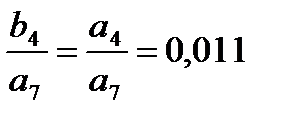 ;
; 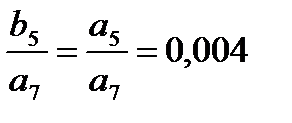 ;
; 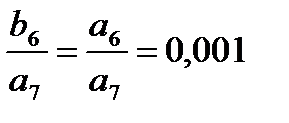 .
.
Такий спосіб використовують для описання нефорсованих систем керування, коли немає необхідності визначати похідні від вхідних впливів. Ця задача ускладнюється при випадковому характері сигналу. У загальному випадку форсованих систем керування, коли серед коренів є не тільки полюси, але і нулі використовують інший спосіб завдання перемінних стану.
Уводиться нова система рівнянь:
y = y1 + 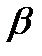 0x 0x
|
ý 1 = y2 + 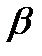 1x 1x
|
ý 2 = y3 + 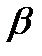 2x 2x
|
| ... |
ý n-1 = yn + 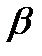 n-1x n-1x
|
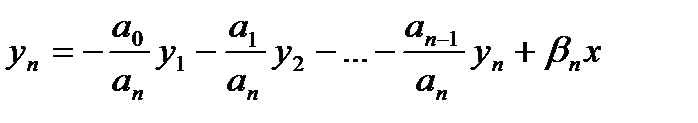
|
Ý = AY + Bu
Y = CY  x = y1 + x = y1 +  x x
|
(4.49)
де Y=[y1, y2, ..., yn]т – матриця-стовпець перемінних стану системи;
A, B – матриці розмірами (n x n) і (n x 1) відповідно, що характеризують структуру і параметри системи;
C-матриця, що відбиває зв'язок перемінних стану Y з вихідним сигналом системи. Оскільки система має один вихід, то C=[100...0].
Матриця стану А відображає динаміку вільної складової стану системи, а матриця В-вплив вхідного сигналу.Порівнюючи системи можна знайти відношення матриці А:
| ... | ... | ... | ... | |||
| A = | ... | |||||
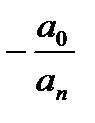
| 
| ... | 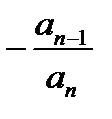
| |||
Знайдемо елементи матриці В. Для цього як приклад розпишемо (4.49) для випадку d = n = 2:
y = y1 - 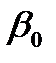 x; y = y1 -
x; y = y1 - 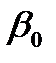 x; (4.50)
x; (4.50)
ý1 = y2 + 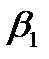 x; y2 = ý1 -
x; y2 = ý1 - 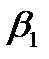 x = ý -
x = ý - 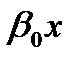 -
- 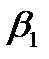 x ; (4.51)
x ; (4.51)
ý2 = 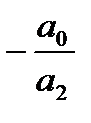 y1 -
y1 - 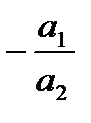 y2 +
y2 +  x; (4.52)
x; (4.52)
Підставимо формули (4.51) та (4.50) у вираження (4.52), тоді:
y// -  x// -
x// - 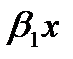 =
= 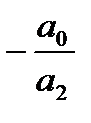 ( y1 -
( y1 - 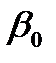 x)
x) 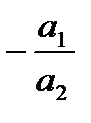 ( ý -
( ý - 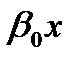 -
- 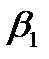 x) +
x) + 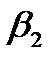 x;
x;
y// - 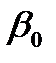 x// -
x// - 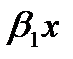 =
= 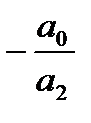 y1
y1 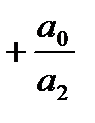
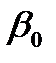 x
x 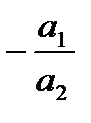 ý
ý 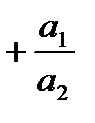
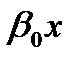
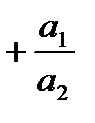 +
+ 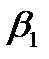 x +
x + 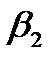 x;
x;
a2y//+a1ý+a0y=a2 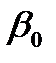 x//+
x//+ 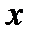 (a1
(a1 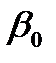 +
+ 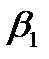 a2)+ x(a1
a2)+ x(a1 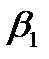 + a2
+ a2 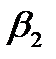 + a0
+ a0 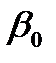 ); (4.53)
); (4.53)
Складемо систему рівнянь:
| a2 b0 = b2; | b0 = b2/a2; | b0 = bn/an; | (4.54) |
| a1 b0 + b1a2 = b1; | b1=(b1 - a1 b0)/a2; | b1=(bn-1–an- b0)/an; | |
| a1b1+a2b2+ a0b0=b0; | b2=(b0 - a1b1 + a0 b0)/a2; | b2=(b0–an-1b1+an2b0)/an |
Рішення для випадку n=d=3 дає:
| b0= b3/a3; | b0= bn/an | (4.55) |
| b1= (b2 – a2 b0)/a3; | b1= (bn-1 – an-1 b0)/an; | |
| b2= (b1 – a2 b1 - a1 b0 )/a3 | b2= (bn-2 – an-1 b1 - an-2 b0 )/an | |
| b3= (b0 – a2 b2 - a1 b1 - a0 b0 )/a3 | b3=(b0– an-1 b2 - an-2 b1 - an-3 b0 )/an |
Узагальнюючи (4.54) і (4.55) можна одержати формули для елементів матриці В=[ 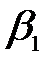 ,
, 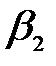 ,…,
,…, 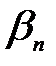 ] для будь-якого n (якщо d<n, то просто деякі b виявляться рівними нулю):
] для будь-якого n (якщо d<n, то просто деякі b виявляться рівними нулю):
| b1 | (bn-1 – an-1 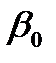 )/an )/an
| (4.56) | |||
| b2 | (bn-2– an-1 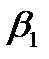 - an-2 - an-2 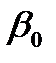 )/an )/an
| ||||
| B= | b3 | = | (b0–an-1 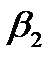 -an-2 -an-2 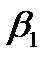 -an-3 b0)/an -an-3 b0)/an
| 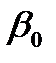 = bn/an = bn/an
| |
| ... | ... | ||||
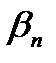
| (b0–an-1bn-1-an-2bn-2-...-a0b0)/an |
Представимо систему через рівняння стану: Представимо систему через рівняння стану:
| a0 = 1 | ||||||||
| a1 = 3.328 | ||||||||
| a2 = 3.709 | ||||||||
| A = | a3 = 3.028 | |||||||
| a4 = 1.050 | ||||||||
| a5 = 0.376 | ||||||||
| -0.01 | -0.023 | -0.027 | -0.02 | -0.011 | -0.004 | -0.001 | a6 = 0.087 a7 = 0.01 | |
| для A2/a2 = 40 дБ |
| 8.700 | ||
| -38.090 | ||
| 109.263 | ||
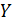 = =
| -229.067 | 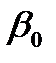 = 0 = 0
|
| 390.680 | ||
| -657.300 | ||
| 1317.078 |
Особливість такого вибору перемінних стану полягає а відсутності необхідності обчислення похідних вхідного сигналу для форсованих систем, що істотно спрощує структуру системи. У цьому випадку можна реалізувати будь-яку систему керування за допомогою набору з інтегральних, пропорційних ланок і суматорів.
Контрольні запитання
1.Що таке фільтр? Для чого він потрібен?
2.Для чого потрібен зворотній зв’язок у системі фільтрації?
3.Що таке перешкода, чи завжди вона присутня у системах обробки інформації?
4.В чому полягає методика Ван-Тріса?
5.Кореляція між сигналом та перешкодою.Її значення.
6.Що таке АКФ?
7.Що дозволяє зробити пряме та зворотнє перетворення Фур’є, Лапласа?
8.Фізичний зміст спектральної щільності сигналу.
9.Для чого необхідний перехід від параметру р до ω?
10.Від чого залежить передатна функція системи?
11.Що собою уявляє система фільтрації n-го порядку?
12.Призначення операцій факторизації та сепарації.
13.Охарактеризувати основні статистичні характеристики сигналів.
14.Представити графічно стаціонарний та нестаціонарний процес.
15.Для чого необхіний зворотній зв’язок у системах керування.
16.На що впливає порядок фільтра?
17.Від чого залежить якість системи керування?
18.В чому відмінність формул Ван-Тріса та Віннера-Хопфа?
Дата добавления: 2015-03-03; просмотров: 1390;
