Применение в расчетах риска вероятностных структурно-логических моделей

Любая опасность реализуется, принося ущерб, благодаря какой-то причине или нескольким причинам.

Реальных опасностей без причин не существует, поэтому предотвращение опасностей или защита от них возможны только при выявлении причин.

Между реализовавшимися опасностями, в дальнейшем событиями, и причинами существует причинно-следственная связь: опасность есть следствие некоторой причины, которая, в свою очередь, является следствием другой причины и т.д.

Таким образом, события и причины образуют иерархические, цепные структуры или системы. Графическое изображение таких зависимостей представляет собой ветвящееся дерево.

В строящихся деревьях имеются ветви событий и ветви причин, что позволяет отразить диалектический характер причинно-следственных связей.

Разделение этих ветвей нецелесообразно, а иногда и невозможно, поэтому полученные при анализе графические изображения называют «деревьями событий и причин».

Построение «деревьев» является эффективной процедурой выявления причин различных нежелательных событий (аварий, травм и т.п.), которая основывается на дедуктивном анализе событий (от общего к частному). Многоэтапный процесс ветвления «деревьев» требует введения ограничений для определения его пределов. Границы ветвления определяются логической целесообразностью получения новых ветвей.

Структура «дерева событий и причин» включает одно нежелательное событие в вершине дерева (авария, катастрофа, несчастный случай и т.д.), которое соединяется с набором соответствующих событий предпосылок (ошибок, отказов, неблагоприятных воздействий) и образующих определенные цепочечные связи или ветви. «Листьями» на ветвях такого дерева являются предпосылки – инициаторы причинных цепей, детализация которых и дальнейший анализ не целесообразны.

При построении «дерева событий и причин» используют специальные условные обозначения событий и логические элементы (вентили), которые иллюстрируют взаимодействие между ними. Форма условных обозначений обеспечивает наглядность и облегчает процесс построения дерева.

Условные обозначения событий, которые используются при построении «дерева событий и причин» приведены в таблице 2.3.

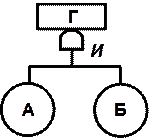
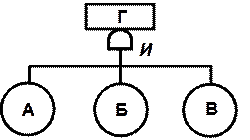
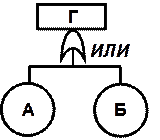
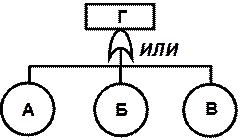
Связь событий в дереве осуществляется с помощью двух основных логических элементов «И» и «ИЛИ», которые подразумевают определенные математические действия по вычислению вероятностей (табл.2.4).

Поскольку все рассматриваемые события и условия их возникновения являются случайными, то для расчета реализации главного события используют определения и зависимости теории вероятностей. Приведем основные из них.

Под событием понимается факт, который в результате опыта может произойти или не произойти.

Вероятность события (Р) – численная мера объективной возможности этого события.

Достоверное событие – событие, которое в результате опыта обязательно должно произойти (Р = 1).

Невозможное событие – событие, которое в результате опыта не может произойти (Р = 0).

Единица измерения вероятностей или диапазон изменения вероятностей – числа от 0 до 1 (0 < Р < 1). .

Таблица 2.3

№ Условное обозначение Название события Главное событие – заглавие дерева событий и причин, заранее определенное нежелательное событие Верхнее событие – промежуточное событие подразумевающее дальнейший анализ. Базисное событие – событие, которое не требует дальнейшего анализа. Трансфер (неописанное продолжение) – событие, которое уже учитывалось в данном дереве событий и причин

Таблица 2.4

№ Условное обозначение Логический элемент (оператор) «И» - логическое произведение (конъюнкция). Указывает, что для получения данного выхода необходимо выполнить все условия на входе. Перед тем, как произойдет событие Г, должны произойти события А и Б либо АБВ. «ИЛИ» - логическая сумма (дизъюнкция). Указывает, что для получения данного выхода должно быть выполнено хотя бы одно из условий на входе. Означает, что событие Г будет иметь место, если произойдет: для двух - хотя бы одно из событий А или Б (или оба); для трех – А или Б или В (или три события вместе).

События А и Б называются независимыми, если появление одного из них не влияет на вероятность появления другого.

Вероятность произведения независимых событий вычисляется по формулам

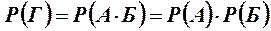; (2.2)

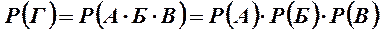. (2.3)

Несколько событий называются несовместными в данном опыте, если они не могут появиться вместе (выпадение орла или решки при подбрасывании монеты; попадание и промах при одном выстреле; пожар в присутствии хозяина и без хозяина; инфицирование гриппом в результате эпидемии и в результате простуды).

К любому числу несовместных событий применима теорема сложения вероятностей

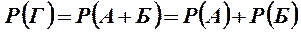; (2.4)

. (2.5)

В случае когда события совместны, вероятность суммы этих событий выражается формулами

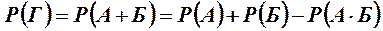; (2.6)

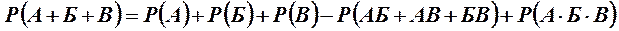.(2.7)

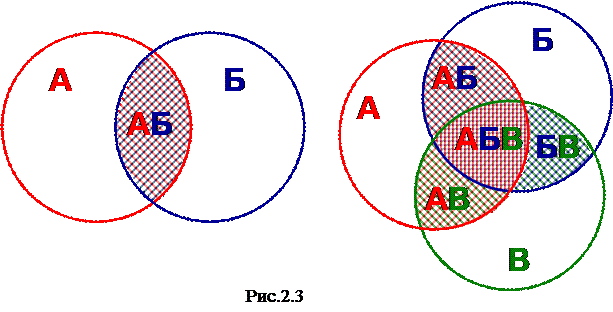
В справедливости формул (2.6-2.7) можно убедиться рассматривая рис. 2.3

В качестве примера рассмотрим алгоритм построения «дерева событий и причин» для технологического процесса с использованием взрывоопасных газов, которые хранятся в баллонах (рис.2.4).

Построение начинается с главного события – взрыва газового баллона, и продолжается поиском всех комбинаций событий, которые могут привести к наступлению главного.

Возникновение опасных ситуаций в виде пяти верхних событий (2 - 6) определяет девять базисных событий (7-15).

Поскольку все события и условия их возникновения являются случайными, то для расчета вероятности реализации взрыва газового баллона используют основные выражения теории вероятности.

Вероятности наступления событий 7-15, т.е. базисных событий, определяют эмпирично или оценивают статистическими методами. Вероятности верхних событий рассчитывают по формулам (2.2-2.7) в соответствии с логикой их реализации, а именно:

- первая причина по которой может произойти взрыв газового баллона - образование источника возгорания (2), одним из событий, которое этому предшествует, является ошибка проекта электрооборудования (4) в результате чего может возникнуть искра в выключателе освещения (8) или искра в электродвигателе вентилятора (9) установленного в помещении где непосредственно выполняется технологический процесс с использованием взрывоопасных газов. При этом события (8, 9) независимые, связаны логическим оператором «ИЛИ» и являются совместными (появления их одновременно хоть и является событием практически невозможным потому что имеет ничтожно маленькое значение вероятности, но все же является событием достоверным). В соответствии с (2.6) запишем

Р₄ = Р₈ + Р₉ – (Р₈ · Р₉).

Р₂ = Р₇ + Р₄ + Р₁₀ – (Р₇ · Р₄ + Р₇ · Р₁₀ + Р₄ · Р₁₀) + (Р₇ · Р₄ · Р₁₀ );

- другой причиной приводящей к взрыву газового баллона, является образование взрывоопасной смеси (3) в результате вытекания газа из баллона (5) и отсутствии при этом вентиляции (6).

Вытекание газа может произойти по причине дефекта (брака) в конструкции самого баллона (11), в случае если не полностью закрыта запорная арматура (12) и в случае несоблюдения необходимых условий хранения (13), таких как температура, влажность, вибрация и т.д. События (11, 12, 13) независимые, связаны логическим оператором «ИЛИ» и являются совместными, тогда с учетом (2.7)

Р₅ = Р₁₁ + Р₁₂ + Р₁₃ – (Р₁₁ · Р₁₂ + Р₁₁ · Р₁₃ + Р₁₂ · Р₁₁₃) + (Р₁₁ · Р₁₂ · Р₁₃ ).

Причиной отсутствия работающей вентиляции может быть либо просто не включение вентилятора (14) из-за невнимательности персонала или сбоя в работе автоматики, либо неисправность непосредственно этого узла системы (15). При этом события (14, 15) независимые, связаны логическим оператором «ИЛИ» и являются несовместными (появления их одновременно событие невозможное). Для определения вероятности события (6) используем формулу сложения вероятностей (2.4)

Р₆ = Р₁₄ + Р₁₅ .

События (5, 6) позволяют определить вероятность верхнего события (3). Т.к. образование взрывоопасной смеси возможно только при условии обязательного выполнения двух событий - они являются совместными и связанными логическим оператором «И». На основании (2.2) получим

Р₃ = Р₅ · Р₆ .

- значения вероятностей верхних событий (2, 3) дают возможность определить вероятность главного события (1) – взрыв газового баллона. В этой ситуации они являются совместными и связанными логическим оператором «И», потому что необходимым условием возникновение взрыва является как наличие взрывоопасной смеси так и источника возгорания.

Таким образом вероятность главного события равна

Р₁ = Р₂ · Р₃ .

На основании приведенного примера, можно сделать вывод про универсальность метода построения «деревьев опасностей и причин» для расчета рисков в разных социально-экономических и технических системах. Конечно при этом необходимы числовые данные наблюдений, большая выборка, значение вероятностей базисных событий, но этот факт не может быть отнесен к недостаткам метода, потому что их всегда можно получить экспертным путем и различными статистическими методами.