ПРИМЕРЫ. Пример1.1. Нелинейные сопротивления и , включенные последовательно в электрическую цепь постоянного тока (рис
Пример1.1. Нелинейные сопротивления 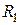 и
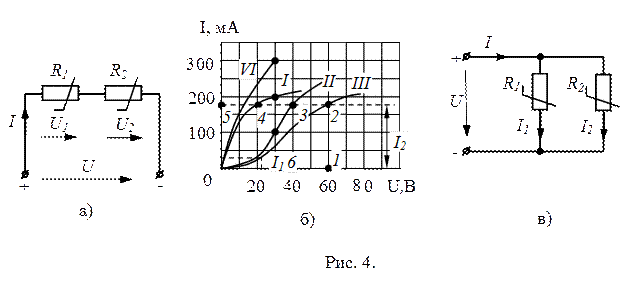
и 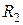 , включенные последовательно в электрическую цепь постоянного тока (рис. 4, а), имеют вольт-амперные характеристики
, включенные последовательно в электрическую цепь постоянного тока (рис. 4, а), имеют вольт-амперные характеристики 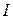 и
и 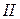 , приведенные на рис. 4, б. Определить ток
, приведенные на рис. 4, б. Определить ток 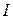 в цепи и напряжения
в цепи и напряжения 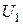 и
и 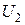 на этих сопротивлениях, если приложенное к цепи напряжение
на этих сопротивлениях, если приложенное к цепи напряжение 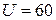 В. В каких пределах измениться напряжение
В. В каких пределах измениться напряжение 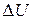 цепи при изменении тока
цепи при изменении тока 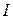 от
от 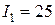 мА до
мА до 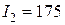 мА?
мА?
Решение. Строят общую вольт-амперную характеристику 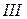 указанных двух последовательно соединенных нелинейных элементов (рис. 4, б) исходя из условия, что подводимое к цепи напряжение
указанных двух последовательно соединенных нелинейных элементов (рис. 4, б) исходя из условия, что подводимое к цепи напряжение  при данном токе
при данном токе 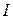 нагрузки равно сумме напряжений на сопротивлениях
нагрузки равно сумме напряжений на сопротивлениях 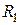 и
и 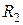 , т.е.
, т.е. 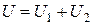 .
.
Ток в цепи при напряжении 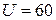 В согласно зависимости
В согласно зависимости 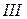 определяется ординатой
определяется ординатой 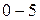 , соответствующей
, соответствующей 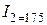 мА.
мА.
Напряжение на участках цепи находят из графических зависимостей. При токе 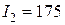 мА
мА 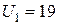 В (абсцисса 5-4),
В (абсцисса 5-4), 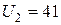 В (абсцисса 5-3). При токе
В (абсцисса 5-3). При токе 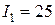 мА напряжение, подводимое к цепи,
мА напряжение, подводимое к цепи, 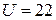 В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рис. 4, б составляет:
В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рис. 4, б составляет: 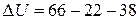 В.
В.
Пример1.2. В электрическую цепь постоянного тока (рис. 4, в) при напряжении 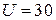 В включены параллельно нелинейные сопротивления
В включены параллельно нелинейные сопротивления 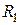 и
и 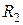 , вольт-амперные характеристики
, вольт-амперные характеристики 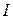 и
и 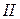 которых представлены на рис. 1, б. Определить общий ток
которых представлены на рис. 1, б. Определить общий ток 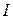 в цепи, токи
в цепи, токи 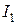 и
и 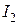 в ветвях.
в ветвях.
Решение. Общая вольт-амперная характеристика 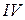 (рис. 4, б) при параллельном соединении нелинейных сопротивлений построена сложением токов (ординат) зависимостей
(рис. 4, б) при параллельном соединении нелинейных сопротивлений построена сложением токов (ординат) зависимостей 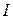 и
и 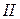 при соответствующем напряжении. Ток нелинейного сопротивления
при соответствующем напряжении. Ток нелинейного сопротивления 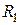 (рис. 4, а) при заданном напряжении
(рис. 4, а) при заданном напряжении 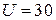 В равен ординате
В равен ординате 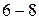 :
: 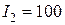 мА. Общий ток в неразветвленной части цепи равен ординате
мА. Общий ток в неразветвленной части цепи равен ординате 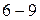 :
: 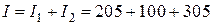 мА.
мА.
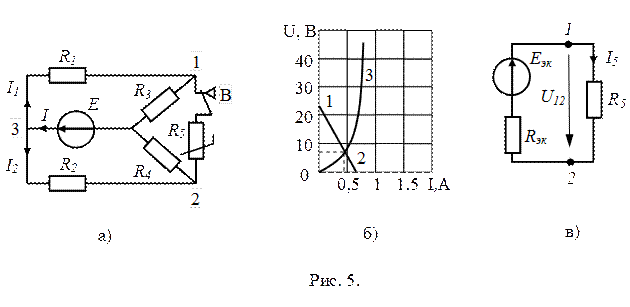
Пример1.3. В электрическую цепь постоянного тока (рис. 5, а) включено нелинейное сопротивление 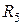 . Определить ток
. Определить ток 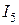 в нелинейном сопротивлении и напряжение
в нелинейном сопротивлении и напряжение 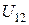 , действующее между точками
, действующее между точками 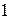 и
и 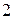 цепи. Вольт-амперная характеристика нелинейного сопротивления
цепи. Вольт-амперная характеристика нелинейного сопротивления 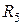 (кривая 3) приведена на рис. 5, б. ЭДС источника питания
(кривая 3) приведена на рис. 5, б. ЭДС источника питания 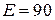 В, сопротивление резисторов:
В, сопротивление резисторов: 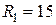 Ом;
Ом; 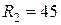 Ом;
Ом; 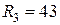 Ом;
Ом; 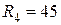 Ом.
Ом.
Решение. Используя метод эквивалентного генератора, определяем напряжение 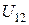 , действующее между точками
, действующее между точками 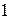 и
и 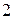 электрической цепи в режиме холостого хода при отключенном нелинейном сопротивлении
электрической цепи в режиме холостого хода при отключенном нелинейном сопротивлении 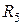 (рис. 5, а).
(рис. 5, а).
Ток в ветви резистора 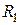 при отключенном нелинейном сопротивлении
при отключенном нелинейном сопротивлении 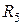 (выключатель В выключен):
(выключатель В выключен): 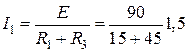 А.
А.
Ток в ветви резистора 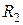 при отключенном нелинейном сопротивлении
при отключенном нелинейном сопротивлении 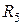 :
: 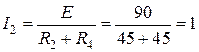 А.
А.
ЭДС эквивалентного генератора 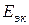 определяют при отключенном нелинейном сопротивлении
определяют при отключенном нелинейном сопротивлении 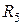 . По второму закону Кирхгофа из уравнения электрического равновесия, составленного для внешнего замкнутого контура электрической цепи (рис. 5, а):
. По второму закону Кирхгофа из уравнения электрического равновесия, составленного для внешнего замкнутого контура электрической цепи (рис. 5, а):
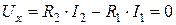 или
или 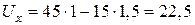 В, откуда
В, откуда 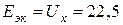 В.
В.
Внутреннее сопротивление 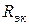 эквивалентного генератора относительно точек
эквивалентного генератора относительно точек 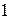 и
и 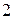 электрической цепи рис. 5, а, при закороченном источнике ЭДС
электрической цепи рис. 5, а, при закороченном источнике ЭДС 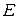 :
: 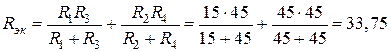 Ом.
Ом.
В соответствии со схемой замещения рассматриваемой нелинейной электрической цепи (рис. 5, в) исходя из уравнения, составленного по второму закону Кирхгофа, имеем: 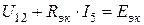 , отсюда
, отсюда 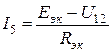 .
.
Полученное уравнение представляет аналитическое выражение зависимости 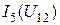 . Поскольку ЭДС
. Поскольку ЭДС 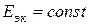 и
и 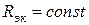 , последнее уравнение является уравнением прямой в системе координат
, последнее уравнение является уравнением прямой в системе координат 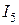 и
и 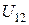 (рис. 5, б, точка 1), проходящей через точки с координатами, которые определяются в режиме холостого хода (при
(рис. 5, б, точка 1), проходящей через точки с координатами, которые определяются в режиме холостого хода (при 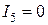 ;
; 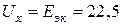 В) и в режиме короткого замыкания (
В) и в режиме короткого замыкания ( 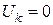 ), ток
), ток 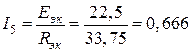 А (точка 2).
А (точка 2).
Ток 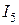 в цепи нелинейного сопротивления
в цепи нелинейного сопротивления 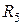 и напряжение
и напряжение 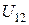 на его зажимах определяют графическим способом как координаты точек пересечения вольт-амперной характеристики нелинейного элемента
на его зажимах определяют графическим способом как координаты точек пересечения вольт-амперной характеристики нелинейного элемента 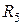 (рис. 5, б) с полученной прямолинейной зависимостью
(рис. 5, б) с полученной прямолинейной зависимостью 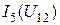 . При этом
. При этом 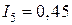 А;
А; 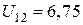 В.
В.
Пример1.4. Для точки 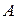 вольт-амперной характеристики
вольт-амперной характеристики 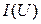 нелинейного элемента (рис. 6) определить статическое
нелинейного элемента (рис. 6) определить статическое 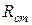 и дифференциальное
и дифференциальное 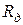 сопротивления.
сопротивления.
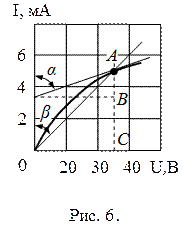
Решение. Статическое сопротивление, соответствующее точке 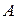 вольт-амперной характеристики:
вольт-амперной характеристики: 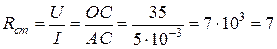 кОм. Статическое сопротивление пропорционально тангенсу угла
кОм. Статическое сопротивление пропорционально тангенсу угла 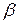 , т.е.
, т.е. 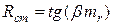 , где
, где 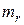 - масштаб сопротивлений.
- масштаб сопротивлений.
Дифференциальное сопротивление, соответствующее вольт-амперной характеристики: 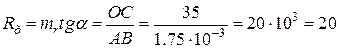 кОм. Дифференциальное сопротивление пропорционально тангенсу угла
кОм. Дифференциальное сопротивление пропорционально тангенсу угла 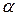 .
.
Дата добавления: 2015-01-13; просмотров: 4224;
