Лабораторна робота №89
ВИВЧЕННЯ ТЕМПЕРАТУРНОЇ ЗАЛЕЖНОСТІ ОПОРУ НАПІВПРОВІДНИКА І ВИЗНАЧЕННЯ ЙОГО ЕНЕРГІЇ АКТИВАЦІЇ
Мета роботи: ознайомитись з основами зонної теорії твердого тіла, дослідити температурну залежність опору власного напівпровідника та визначити його енергію активації.
Прилади і матеріали: цифровий омметр, логометр, нагрівна піч, термостійка пробірка, термоопір, дослідницький напівпровідник.
1 ТЕОРЕТИЧНІ ВІДОМОСТІ
1.1 Зонна теорія твердого тіла
Розглянемо процес утворення кристала з ізольованих атомів. Якщо атоми перебувають на великих відстанях один від одного, то схеми їх енергетичних рівнів повністю ідентичні. При цьому їх заповнення електронами здійснюється в кожному атомі незалежно від заповнення аналогічних рівнів в інших атомах. При утворенні кристалу, по мірі зближення атомів між ними посилюється взаємодія, яка і обумовлює зміну положення енергетичних рівнів. Замість одного ідентичного рівня для всіх N атомів, які утворюють кристал, виникає N щільно розміщених підрівнів. Таким чином, кожний енергетичний рівень атома розширюється, зміщується і розщеплюється в кристалі на N дуже близьких підрівнів, які утворюють енергетичну зону.
Ступінь розширення зони для різних енергетичних рівнів не однакова. Більш інтенсивно збурюються рівні, заповнені в атомі зовнішніми (валентними) електронами. Тому відповідні енергетичні зони порівняно широкі. Рівні, заповнені внутрішніми електронами, які сильніше зв’язані з ядром, зазнають тільки незначних збурень від інших атомів, внаслідок чого їх енергетичні рівні в кристалі утворюють вузькі енергетичні зони. На рис. 89.1 показано розщеплення енергетичних дискретних рівнів ізольованих атомів і утворення енергетичних зон при зменшенні відстані r між сусідніми атомами. Із зонної схеми видно, що розщеплення рівнів, яке спостерігається для внутрішніх електронів, досить мале. Інтенсивно розщеплюються тільки вищі енергетичні рівні, зайняті зовнішніми валентними електронами.
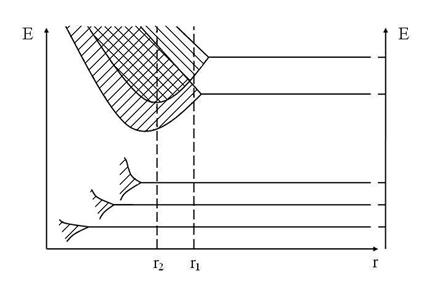
Рисунок 89.1
Ступінь заповнення електронами енергетичних підрівнів у зоні визначається заповненням відповідного рівня в ізольованому атомі. Із незайнятих рівнів утворюються вільні енергетичні зони, із частково заповнених – частково заповнені енергетичні зони. В загальному випадку можна говорити про 3 типи енергетичних зон в твердому тілі: валентну зону, зону провідності (вільну зону) та заборонену зону. Валентна зона утворюється із енергетичних рівнів внутрішніх (зв’язаних) валентних електронів вільних атомів. Зона провідності (вільна зона) або частково заповнена електронами, або вільна і утворена із енергетичних рівнів зовнішніх “колектизованих” вільних електронів ізольованих атомів. Валентна зона I і зона провідності II є дозволеними і розділені забороненою зоною III (рис.89. 2).
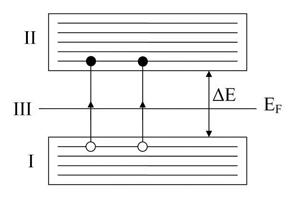
Рисунок 89.2
В забороненій зоні електрони не можуть перебувати. Таким чином, заборонена зона – це сукупність значень енергії, яких не можуть набувати електрони в твердому тілі. Ширина енергетичних зон не залежить від розмірів кристала. Дозволені зони (валентна і вільна) тим ширші, чим слабший зв’язок валентних електронів із ядрами.
Зонна теорія твердого тіла дає змогу з єдиної точки зору пояснити існування металів, діелектриків і напівпровідників, інтерпретуючи відмінності їх електрофізичних властивостей неоднаковим заповненням електронами дозволених енергетичних зон та шириною забороненої зони. Відмінність між металами і діелектриками з точки зору зонної теорії полягає в тому, що при температурі T = 0K в зоні провідності металів є електрони, а в зоні провідності діелектриків вони відсутні. Різниця ж між діелектриками і напівпровідниками визначається шириною забороненої зони: для діелектриків вона досить широка (>1еВ), а для напівпровідників – досить вузька (<1еВ).
В залежності від внутрішньої будови твердого тіла рівноважна відстань між сусідніми атомами в кристалі може бути або типу r1 (для діелектриків і напівпровідників), або типу r2 (для металів) (рис. 89.1). При відстанях типу r1 між валентною зоною і зоною провідності існує заборонена зона. При відстанях типу r2 відбувається перекривання валентної зони і зони провідності, тобто немає забороненої зони. Зонну структуру енергетичного спектру твердого тіла можна отримати безпосередньо із розв’язку рівняння Шредінгера для електрона, який рухається в періодичному силовому полі кристалічної гратки.
1.2 Електрофізичні властивості власних напівпровідників
Всі напівпровідникові матеріали можна розділити на дві групи – власні і домішковінапівпровідники. Власними напівпровідниками є хімічно чисті елементи (Ge, Si, Se) а також хімічно чисті сполуки (InSb, GaAs, CdS) та ін. Одним із найбільш поширених напівпровідникових елементів є кремній, який має кристалічну структуру типу алмазу, в якій кожний атом з’єднаний ковалентними зв’язками з чотирма найближчими сусідніми атомами. Спрощена плоска схема розміщених атомів в кристалі зображена на рис. 3, де кожна риска позначає ковалентний зв’язок, здійснюваний одним електроном. В ідеальному кристалі при температурі T = 0K така структура є діелектриком, оскільки всі валентні електрони утворюють хімічні зв’язки і, таким чином, не існує вільних зарядів. При підвищенні температури(або під дією інших зовнішніх факторів) теплові коливання гратки можуть обумовлювати розрив деяких ковалентних зв’язків, тобто частина електронів переходить у вільний стан. В покинутому електроном місці утворюється вакансія, яка отримала назву дірки (на рис. 89.3 вона зображена світлим кружечком), заповнити яку можуть електрони із сусідньої пари. В результаті вакансія (дірка), так як і вільний електрон, буде рухатись по кристалу. Рухи електронів провідності і квазічастинок – дірок – при відсутності зовнішнього електричного поля будуть хаотичними. Якщо ж на кристал накласти електричне поле, то електрони почнуть рухатись проти напруженості поля , а квазічастинки (дірки) – за полем, що
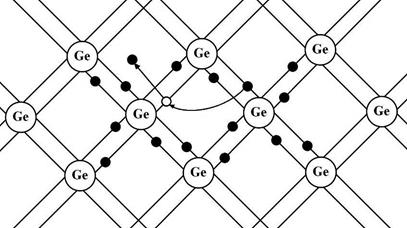
Рисунок 89.3
обумовить власну провідність напівпровідника. Провідність власних напівпровідників, обумовлена вільними електронами, називається електронною провідністю (провідність n-типу). Електропровідність власних напівпровідників, обумовлена квазічастинками (дірками), називається дірковою провідністю (провідність p-типу). Отже, у власних напівпровідниках є два механізми провідності – електронна і діркова. Кількість електронів в зоні провідності рівна кількості дірок у валентній зоні.
Провідність напівпровідників завжди є збудженою, тобто проявляється тільки під дією зовнішніх факторів (температури, опромінення, сильних електричних полів і т.д.). У власному напівпровіднику рівень Фермі EF знаходиться посередині забороненої зони (рис.89.2). Рівень Фермі – це особливий енергетичний рівень. Його специфіка полягає в тому, що при температурі T = 0K він повністю заповнений електронами. Вищі енергетичні рівні при цій температурі є порожніми. При вищій температурі (T > 0K) ймовірність заповнення електронами рівня Фермі становить 50%.
Для переходу електрона з верхнього рівня валентної зони на нижній рівень зони провідності затрачається енергія активації, яка рівна ширині ΔE забороненої зони (рис.89.2). При появі електрона в зоні провідності у валентній зоні виникає дірка. Отже енергія, затрачена на утворення пари носіїв струму, повинна ділитись на дві рівні частини. Тому енергія, яка відповідає половині ширини забороненої зони, іде на перекидання електрона і така ж сама енергія затрачається на утворення дірки. Початок відліку кожного з цих процесів повинен знаходитись посередині забороненої зони. Енергія Фермі у власному напівпровіднику – це енергія, від якої відбувається збудження електронів і дірок.
Температурна залежність опору R0 власного напівпро-відника виражається співвідношенням:
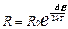 , (89.1)
, (89.1)
де R0 – стала для даного напівпровідника величина, k – стала Больцмана, Т – абсолютна температура. Зменшення опору напівпровідника з підвищенням температури є його характерною особливістю і з точки зору зонної теорії пояснюється дуже просто: при підвищенні температури збільшується кількість електронів, які внаслідок теплового збудження переходять із валентної зони в зону провідності і беруть участь в електропровідності.
Для вивчення температурної залежності опору напівпровідників використовується установка, схема якої подана на рис. 89.4. Досліджуваний напівпровідник 2 міститься в термостаті 6. Термостат нагрівається за допомогою електропечі 1, всередині якої він знаходиться. Для вимірювання електричного опору досліджуваного напівпровідника служить цифровий омметр 5. Вимірювання температури в термостаті здійснюється за допомогою логометра 4. Датчиком температури є термоопір 3, який разом із досліджуваним зразком знаходиться всередині термостата.
Для отримання робочої формули визначення енергії активації А прологарифмуємо формулу (89.1). При цьому отримується співвідношення:
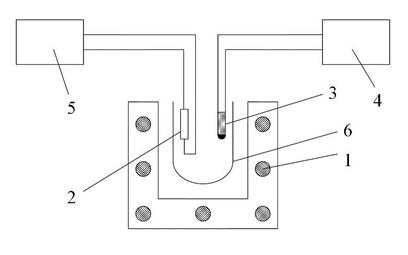
Рисунок 89.4
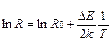 (89.2)
(89.2)
Графіком залежності (2) в координатах ( 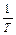 ,
, 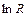 ) є пряма (див. рис. 89.5), кутовий коефіцієнт якої
) є пряма (див. рис. 89.5), кутовий коефіцієнт якої
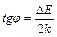 . (89.3)
. (89.3)
Із рис. 89.5 видно, що
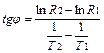 . (89.4)
. (89.4)
Прирівнявши праві частини (3) і (4), отримаємо:
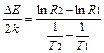 , (89.5)
, (89.5)
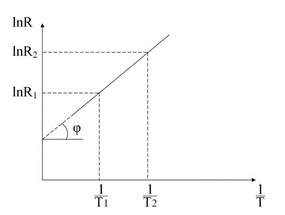
Рисунок 89.5
звідки енергія активації
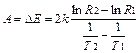 , (89.6)
, (89.6)
або
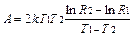 . (89.7)
. (89.7)
Відносна похибка енергії активації
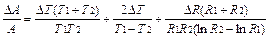 . (89.8)
. (89.8)
Слід звернути увагу, що, згідно позначень на рис.89.5, 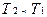 .
.
Дата добавления: 2015-02-19; просмотров: 1127;
