Принцип действия
В основе работы большинства датчиков деформации лежит тензорезистивный эффект – изменение электрического сопротивления датчика при его деформировании. Такие датчики называются тензорезисторами.
Электрическое сопротивление твердого тела изменяется при деформации как за счет изменения геометрических размеров, так и за счет изменения удельного сопротивления материала. В случае одноосного напряжения (например, при растяжении) относительное изменение сопротивления dR/R элемента длиной l с удельным сопротивлением ρ и коэффициентом Пуассона νп равно
dR/R = (1 + 2 νп) dl/l + dρ/ρ. (2.1)
В уравнении (2.1) первое слагаемое определяет изменение геометрии тела, второе – изменение удельного сопротивления. Так как ν 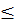 0,5, то приращение сопротивления за счет изменения геометрических размеров не превышает 2dl/l.
0,5, то приращение сопротивления за счет изменения геометрических размеров не превышает 2dl/l.
Приращение сопротивления за счет изменения удельного сопротивления зависит от структуры и свойств материала и может быть в десятки и сотни раз больше, чем за счет геометрии. Принято обозначать 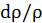 = m dl/l, где m – константа, характеризующая изменение удельного сопротивления при деформации (иногда ее называют тензочувствительностью). При деформации удельное сопротивление твердого тела может изменяться вследствие следующих причин:
= m dl/l, где m – константа, характеризующая изменение удельного сопротивления при деформации (иногда ее называют тензочувствительностью). При деформации удельное сопротивление твердого тела может изменяться вследствие следующих причин:
– изменения взаимодействия между электронами и упругими волнами в кристалле, приводящего к изменению подвижности электронов;
– изменения энергии Ферми, приводящего к изменению числа электронов проводимости;
– изменения зонной структуры вследствие перекрытия, сближения или удаления различных зон;
– возникновения новых кристаллических модификаций.
У большинства металлических материалов (металлов и сплавов) изменение удельного сопротивления в основном обусловлено изменением подвижности электронов при деформации.
Приращения сопротивления металлов и сплавов в области упругой деформации изменяются линейно. Поэтому уравнение (2.1) можно записать в виде
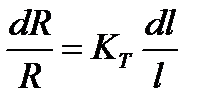 , (2.2)
, (2.2)
где 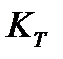 – коэффициент пропорциональности между относительной деформацией
– коэффициент пропорциональности между относительной деформацией 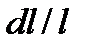 и относительным изменением сопротивления
и относительным изменением сопротивления 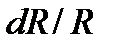 .
.
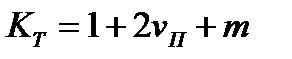 (2.3)
(2.3)
называется коэффициентом тензочувствительности. Для большинства металлов и сплавов в области упругой деформации 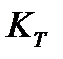 невелик и изменяется от 0,6 до 5,5. В области пластической деформации межатомные расстояния не меняются,
невелик и изменяется от 0,6 до 5,5. В области пластической деформации межатомные расстояния не меняются,  , и тензоэффект определяется только изменением геометрии проводника. Так как в области пластической деформации
, и тензоэффект определяется только изменением геометрии проводника. Так как в области пластической деформации  , то
, то  для всех проводников одинаков и равен 2.
для всех проводников одинаков и равен 2.
В полупроводниковых материалах коэффициент тензочувствительности принимает значения от (–100) до +200, что в значительной степени определяется большой величиной коэффициента m.
Тензочувствительность в полупроводниках зависит от кристаллографического направления, типа проводимости и удельного сопротивления, с ростом которого тензочувствительность растет, рис. 2.1.
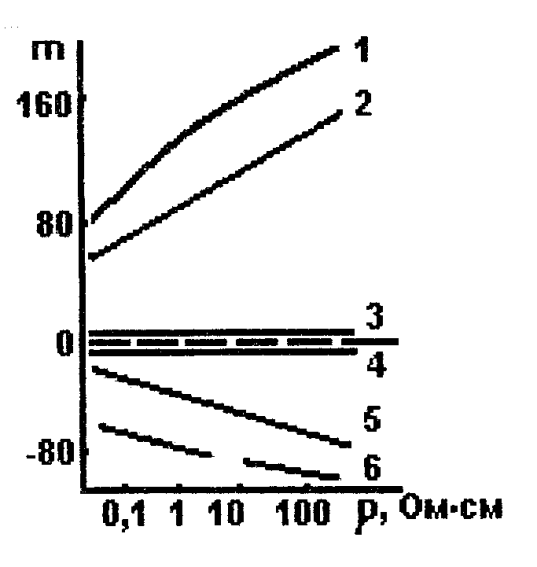
Рис. 2.1. Зависимость тензочувствительности кремния
от удельного сопротивления при различном типе
проводимости и в различных кристаллографических
направлениях: 1 – p-тип, [111]; 2 – р-тип, [110];
3 – р-тип, [100]; 4 – n-тип, [111];
5 – n-тип, [110]; 6 – n-тип, [100]
Причиной изменения удельного сопротивления полупроводника при деформации может быть либо изменение концентрации носителей заряда, либо изменение их подвижности. Для 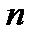 -типа полупроводника
-типа полупроводника
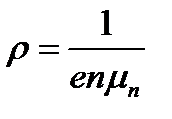 , (2.4)
, (2.4)
где n – концентрация электронов, μn – их подвижность.
При деформации может изменяться либо концентрация, либо подвижность, либо одновременно оба этих параметра.
В полупроводниках изменение концентрации носителей заряда при деформации может быть вызвано изменением ширины запрещенной зоны и энергии ионизации примеси, а также изменениями эффективных плотностей состояний в валентной зоне и зоне проводимости. Однако помимо влияния деформации на концентрацию носителей заряда сильно влияет температура, поэтому при ее изменении тензорезистор будет показывать «кажущуюся» деформацию.
С целью уменьшения влияния температуры на работу тензорезисторов для их изготовления используются сильнолегированные полупроводники, температурный рабочий диапазон которых приходится на участок истощения примесной проводимости (на котором концентрация носителей заряда равна концентрации легирующей примеси, она остается постоянной как при изменении деформации, так и при изменении температуры). Поэтому рассмотрим вторую причину изменения удельного сопротивления при деформации – изменение подвижности, являющуюся основной при объяснении тензоэффекта в полупроводниках.
Высокая тензочувствительность связана со сложной структурой энергетических зон полупроводников, причем тензоэффект в полупроводниках разного типа проводимости имеет различную природу и связан с перераспределением носителей заряда между различными подзонами.
Рассмотрим Si и Ge n-типа проводимости, энергетическая структура которых приведена на рис. 2.2. Зависимость энергии от волнового вектора Е(k) в зоне проводимости имеет несколько минимумов энергии. Соответствующие минимумам изоэнергетические поверхности в k-пространстве являются эллипсоидами вращения, вытянутыми вдоль осей симметрии кристалла. В Si это направления [100], поэтому имеется 6 эквивалентных долин для электронов, в Ge - направления [111], имеются 4 эквивалентные долины. Ввиду несферичности изоэнергетических поверхностей вводятся две эффективные массы для электронов: в продольном 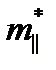 и поперечном
и поперечном 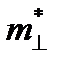 направлениях,
направлениях, 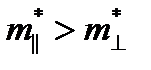 .Так как подвижность
.Так как подвижность 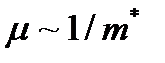 , то и значения подвижностей также различны и
, то и значения подвижностей также различны и 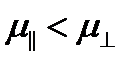 .
.
,. 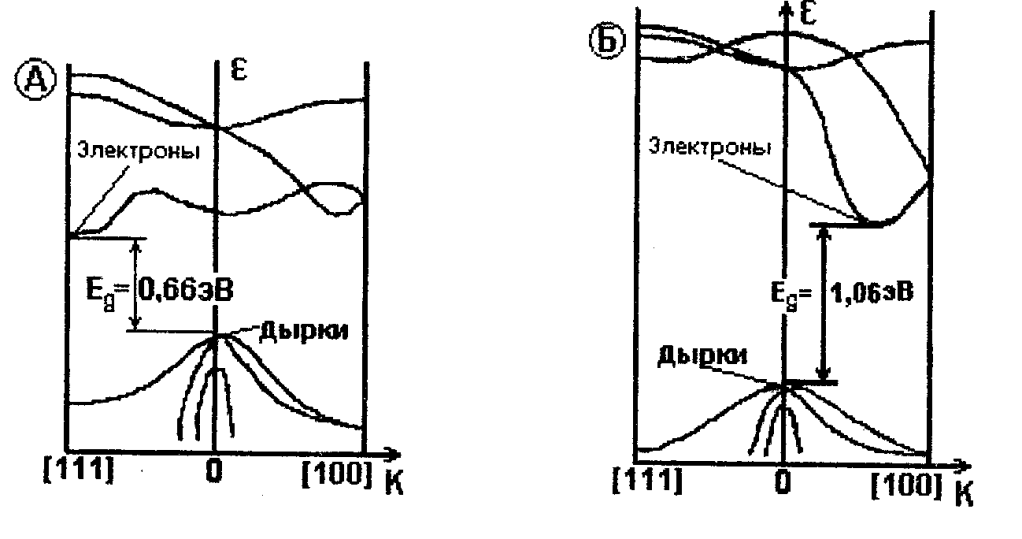
Рис. 2.2. Энергетическая структура германия (А)
и кремния (Б)
В недеформированных кристаллах все долины эквивалентны и концентрация электронов в них одинакова. При приложении одноосной деформации эквивалентность долин может нарушаться, что приведет к перераспределению электронов между ними. Долины, дно которых опустится, дадут больший вклад в проводимость, чем те долины, дно которых поднимется. В условиях анизотропии подвижностей электронов это ведет к изменению проводимости. Например, если сжать кристалл Si вдоль оси [100], то расстояния между атомами в этом направлении уменьшатся, обменный интеграл для этого направления возрастет, а для направлений [010] и [001] уменьшится. Это приведет к тому, что дно зоны проводимости в [100] опустится, а в перпендикулярных направлениях – поднимется, концентрация электронов в [100] возрастет, а в перпендикулярных направлениях уменьшится при сохранении суммарной концентрации во всех долинах.
Рассмотрим перераспределение электронов только между двумя минимумами – в [100] и [010]. При отсутствии деформации электропроводность этих двух минимумов
 0 = e(n1
0 = e(n1 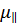 + n2
+ n2 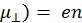 0μ0 , (2.5)
0μ0 , (2.5)
где n1 = n2 = n0/2 – от направления не зависит; n0 – суммарная концентрация электронов; μ0 = 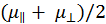 – средняя подвижность.
– средняя подвижность.
При сжатии в [100] n1 увеличивается, а n2 –уменьшаетcя на Δn. Электропроводность при сжатии
σД -= e [(n1 + Δn) 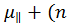 2 – Δn)
2 – Δn) 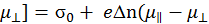 ). (2.6)
). (2.6)
Так как 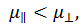 то σД
то σД 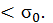 Относительное изменение проводимости
Относительное изменение проводимости
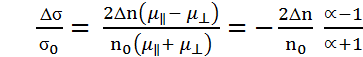 (2.7)
(2.7)
определяется количеством перераспределенных электронов и отношением подвижностей α = 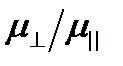 . В Si это отношение равно 5,16; в Ge – 19,3.
. В Si это отношение равно 5,16; в Ge – 19,3.
При сжатии вдоль [111] деформация вдоль осей <100> одинакова, минимумы смещаются в одном и том же направлении на одну и ту же величину, нет переходов электронов из долины в долину, нет и изменения проводимости.
Аналогично можно определить изменение электропроводности при деформации с учетом всех минимумов. Максимальное изменение подвижности происходит при деформации в направлении расположения нижних минимумов: в n-Gе в направлении [111], в n-Si в направлении [100].
В Gе, Si и GаАs р-типа проводимости анизотропии подвижности дырок практически нет. Как видно из рис. 2.1, в вершине валентной зоны соприкасаются две ветви энергии, т.е. вершина валентной зоны является вырожденной. Этим ветвям соответствуют различные эффективные массы дырок, в связи с чем подзону с малой эффективной массой называют подзоной "«легких"» дырок, а большой – «тяжелых». При одноосной деформации нарушается симметрия кристалла, что приводит к снятию вырождения, т.е. подзоны легких и тяжелых дырок смещаются в противоположных направлениях. Это приводит к перераспределению дырок между подзонами. Если
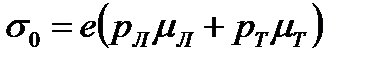 , (2.8)
, (2.8)
где 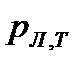 и
и 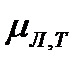 – соответственно концентрация и подвижность легких и тяжелых дырок, то
– соответственно концентрация и подвижность легких и тяжелых дырок, то
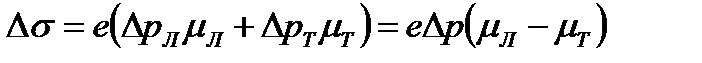 , (2.9)
, (2.9)
так как общая концентрация дырок 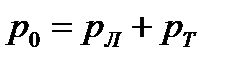 постоянна
постоянна 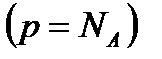 , определяется концентрацией акцепторной примеси и
, определяется концентрацией акцепторной примеси и 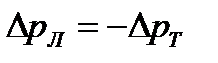 .
.
Относительное изменение проводимости
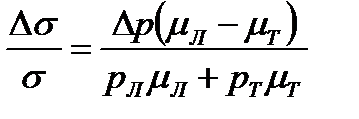 . (2.10)
. (2.10)
Максимальное изменение подвижности дырок Gе, Si и GаАs р-типа проводимости происходит при деформации в направлении [111].
В Gе п- и р-типа проводимости наибольшая тензочувст-вительность наблюдается в направлении [111], в Si n-типа в направлении [100] и в Si р-типа в направлении [111]. Знак тензочувствительности в полупроводниках n-типа отрицательный, а в полупроводниках р-типа – положительный.
Наибольшее значение коэффициента тензочувствительности для Gе и Si порядка 150 – 170. Тензочувствительность GаАs р-типа максимальна в направлении [111] и достигает такой же величины, как в Gе и Si.
Большой тензочувствительностью обладают соединения n-GаSb в направлении [111] ( 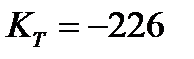 ), p-InSb в направлении [111] (
), p-InSb в направлении [111] ( 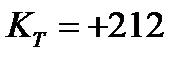 ).
).
.
Дата добавления: 2015-02-16; просмотров: 1638;
