Типовые элементы структурных схем САУ

1.	Звено
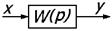
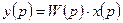
2.	Узел разветвления
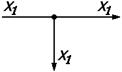
3.	Сумматор
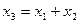
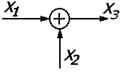
4.	Элемент сравнения

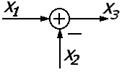
Для упрощения (свертывания) сложных алгоритмических схем применяют три главных правила преобразования, с помощью которых определяют эквивалентные передаточные функции типовых соединений звеньев.

v Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций всех звеньев, входящих в соединение.

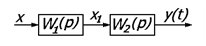Определить передаточную функцию всей системы.

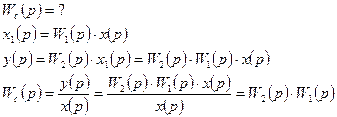
v Передаточная функция параллельно соединенных звеньев равна алгебраической сумме передаточных функций всех звеньев, входящих в соединение.

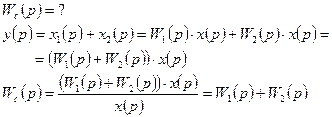
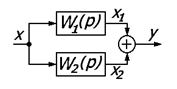
v Передаточная функция соединения с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс (минус) произведение передаточных функций прямой цепи и цепи обратной связи.

Соединение звеньев с отрицательной обратной связью.

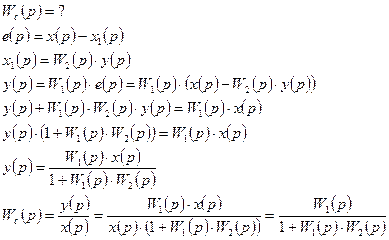
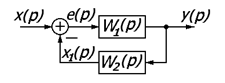
Структурная схема звеньев с положительной обратной связью.

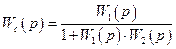
С помощью этих правил удается преобразить любую исходную алгоритмическую схему, не содержащую перекрестных связей, к одноконтурной схеме.

Алгоритмическую схему замкнутой системы управления (и саму систему) называют одноконтурной, если при ее размыкании в какой либо точке образуется цепь, не содержащая параллельных соединений и обратных связей. Цепь, полученная при размыкании замкнутой системы (см. рис. а) между точками А и В, не содержит параллельных соединений и обратных связей.

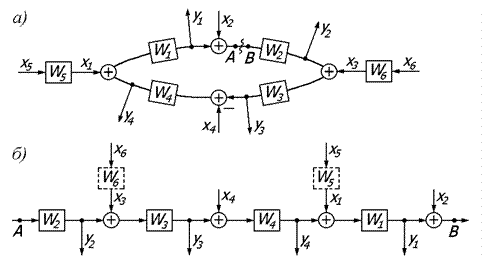Получаемая при размыкании одноконтурной системы цепь последовательно соединенных элементов, стоявших внутри замкнутого контура, называется разомкнутым контуром системы (см. рис. б). В соответствии с этим определением

Передаточная функция разомкнутого контура W_р.к.(р) одноконтурной системы равна произведению передаточных функций всех элементов, стоящих внутри контура системы. Передаточные функции элементов, стоящих вне замкнутого контура, никогда не входят в произведение W_р.к.(р).

Для нашей системы

,

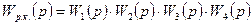передаточные функции W₅(p) и W₆(p) не входят в это произведение, т.к. эти элементы стоят вне замкнутого контура.