Экономическое распределение нагрузки между параллельно работающими агрегатами.
Используя метод множителей Лагранжа можно получить условие наивыгоднейшего распределения нагрузки между агрегатами эл.станции. В виде равенства отнош. первичного ресурса, т.е. приведенной мощности к приращению вторичного ресурса, т.е полезной мощности при соблюдении балансового соотношения.
1. Распределение между агрегатами ТЭС.
агрегаты: турбины, котлы, блоки.
а. Прирост для i-ой турбины 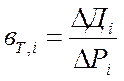
б. Для котла 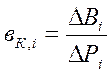
в. 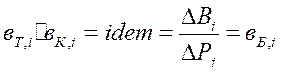
где 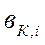 -относительный прирост расхода котла, т.е изменение расхода к изменению паросъема;
-относительный прирост расхода котла, т.е изменение расхода к изменению паросъема;
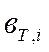 - относительный прирост расхода турбины, т.е отношение изменения расхода пара к изменению мощности турбины;
- относительный прирост расхода турбины, т.е отношение изменения расхода пара к изменению мощности турбины;
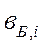 - отношение приращения топлива к изменению отдаваемой в сеть мощности;
- отношение приращения топлива к изменению отдаваемой в сеть мощности;
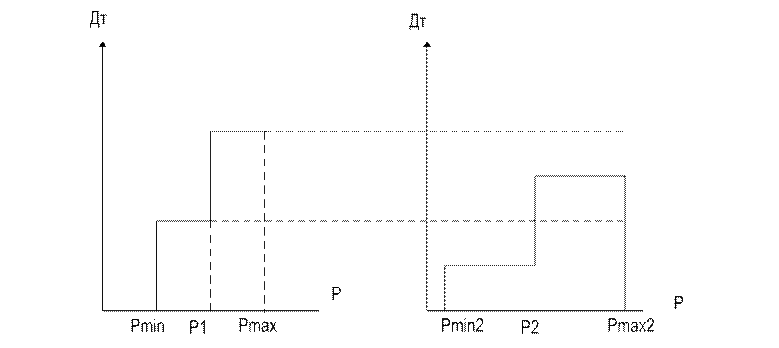
Рmin=Pmin1+Pmin2-
РH>P1+P2 – загруж. блок 2
РH>P1+Pmax2- загруж. блок 1
2. Распределение нагрузки между агрегатами ТЭЦ.
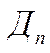 - производственный расход топлива.
- производственный расход топлива.
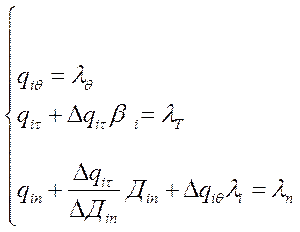
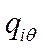 - относительный прирост расхода тепла при производстве эл. мощности;
- относительный прирост расхода тепла при производстве эл. мощности;
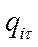 -относительный прирост расхода тепла при изменении величины теплофикационного отбора;
-относительный прирост расхода тепла при изменении величины теплофикационного отбора;
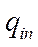 - относительный прирост расхода тепла при изменении производственного отбора.
- относительный прирост расхода тепла при изменении производственного отбора.
3. Распределение нагрузки между агрегатами ГЭС.
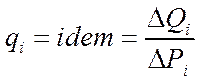
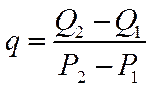
4. Распределение в ЭЭС содержащей АЭС.
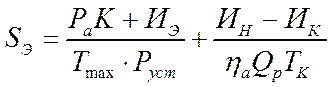
К- капитальные вложения в АЭС; ИЭ- эксплуат. издержки; Ра- норма отчислений на амортиз.; Тмах- число часов, когда АЭС работает с установленной мощностью; ИН,ИК- стоимость ядерного топлива загружаемого в реактор и выгружаемая из него, ТК-прод-сть работы; QP-тепловая мощность реактора; 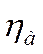 -КПД.
-КПД.
Особенности:
1. Потери АЭС мало зависят от энергетич. нагрузки.
2. Увеличение Тмах снижает себестоимость энергии.
Условие наивыгоднейшего распределения
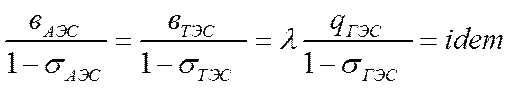
В практических расчетах часто допускают независимое распределение акт. и реакт. нагрузок между станциями ЭС.
Задача распределения реакт. нагрузки может быть решена методом множителей Лагранжа. В качестве критерия оптимальности выберем минимум потерь акт. мощности.
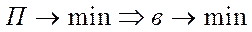
1. Уравнение цели 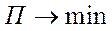 (
( 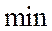 потерь активной мощности).
потерь активной мощности).
2. Уравнение связи 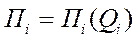 , где i-номер источника реакт. мощности.
, где i-номер источника реакт. мощности.
3. Уравнение ограничения- балансовое уравнение реакт. нагрузок и источников реакт. мощности
4. Уравнение оптимизации 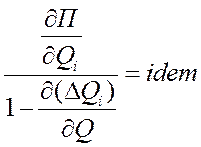
5. Функция Лагранжа 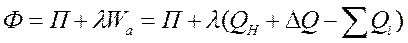
получим: 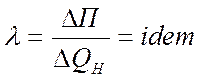 , где QH- приращение реакт. мощности у потребителя при генерации реакт. мощности.
, где QH- приращение реакт. мощности у потребителя при генерации реакт. мощности.
Оптимальным является такой режим, когда для всех источников реакт. мощности будет иметь место равенства потерь акт. мощности 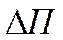 на единицу реакт. мощности у потребителя.
на единицу реакт. мощности у потребителя.
1-9. Общая хар-ка задачи нелинейного программирования. Выбор направления и длины шага в задаче минимизации целевой функции. Рекуррентные выражения.








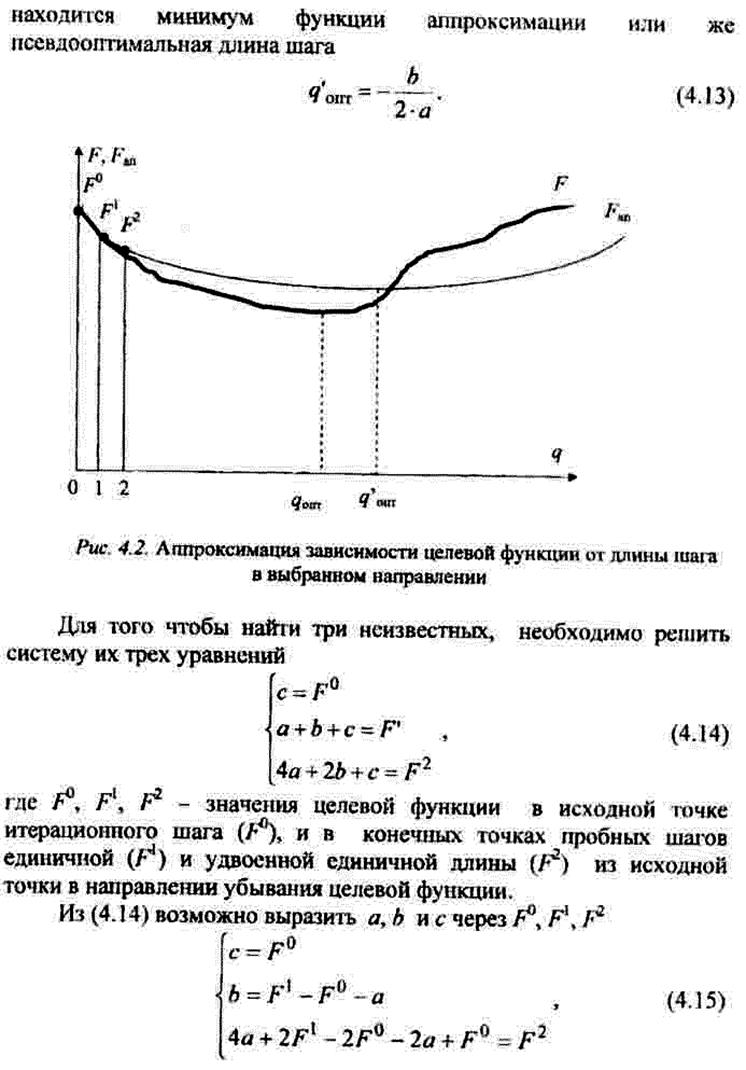

1-10. Общая хар-ка задачи линейного программирования. Симплекс-метод.
Линейное программирование дает возможность нахождения оптимального решения при линейной ф-ции и наличия ограничений.
Пусть матем. модель записана в виде целевой ф-ции, в виде полинома Ц(х)=а1х1+ а2х2+… +аnхn , т.е мы должны найти х1...xn при котором обеспечивалось бы экстремальное значение целевой ф-ции при наличии некоторых ограничений:
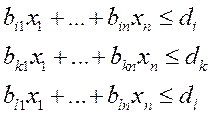
Симплекс-метод- метод лин-го программирования используемый для задач оптимизации при наличии лин-ой выпуклой целевой ф-ции и ограничений в виде линейных неравенств.
Симплекс-метод состоит в отыскании наилучшего плана распределения ограничен. ресурсов, т.е задача заключается в отыскании оптимального плана 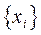 составляющих экстремум целевой ф-ции.
составляющих экстремум целевой ф-ции.
В случае, если n-m=2 каждая из ограничений лин. ур. может быть быть представлена геометрически, а решение получено граф. путем выбора оптимального решения, соответствующего одной из вершин в многоугольнике ограничений. При наличии более чем 2 оптимиз. переменных необходимо использовать алгебраич. методы решения задачи лин. программ.- симплекс-метод.
Однозначное определение экстрем. точек возможно алг. путем, т.е приравнивая к нулю n-m=0 и решение системы из м уравнений, приводящих к базисным решениям. Базисные переменные- переменные, имеющие не нулевые значения.
Допустимые базисн. решения- решения, удовлетворяющие требованию неотрицательности правых частей уравнений.
Начальное решение соответствует началу координат, затем осуществляется переход по границе пространства решений к смежной угловой точке для которой значение целевой ф-ции уменьшается по сравнению с прежним и т.д. вплоть до точки, где целевая ф-ция принимает минимальное значение.
Выполнение в ручную итерационного алгоритма симплекс-метода для большого числа переменных задача трудоемкая с большим числом шагов и поэтому задачи больших размерностей решаются с помощью ЭВМ.
Симплекс-метод:
1- табличный;
2- метод искусственного базиса;
3- модифицированный симплекс-метод.
Задача заключается в том, чтобы найти оптимальный план распределения ограниченных ресурсов, доставляющий экстренум целевой функции:
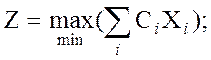
При наличии ограничений: 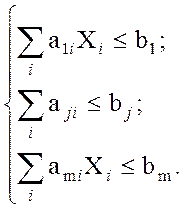 |A||X|<|b|;
|A||X|<|b|;
где j=1…m – число ограничений; i=1…n – число переменных;
Если разность n-m=2, тогда ограничения можно представить геометрически, а решения найти графически: путем выбора оптимального решения соответствующего одной из вершин многоугольника ограничений.
Если число оптимизируемых параметров больше 2, то применяются алгебраические методы, например, симплексный.
Z=ΣCiXi;
В первую очередь система уравнений приводится к канонической или стандартной форме:
1) ограничения-неравенства приводятся к форме равенств с неотрицательной правой частью.
2) все переменные должны иметь положительные значения.
Z – ΣCjXj=0;
ΣAijXj+Si=bi;
где Si – вспомогательные переменные, которые вводятся в ограничения для приведения их в форму равенств (если +, то ≤; а если –, то ≥)
Суть симплексного метода заключается в том, чтобы найти оптимальное решение соответствующее одной из экстремальных точек по определенному алгоритму, уменьшающему число шагов.
Переменные: базисные >0, небазисные =0.
Алгоритм включает три этапа:
0) Матмодель приводится к канонической форме.
1) Из числа небазисных переменных выбирается включаемая переменная, увеличение которой доставляет наискорейшее возрастание ЦФ.
2) Из числа базисных переменных выбираются исключаемые переменные, которые быстрее других стремятся к нулю при переходе к смежной точке.
3) Определяется новое базисное решение.
Составляется симплексная таблица.
Включаемые небазисные переменные определяются по наибольшему отрицательному коэффициенту в Z строке.
Столбец включаемой переменной называется ведущим столбцом k.
Исключаемые переменные определяются по минимальному положительному отношению решения к соответствующему коэффициенту в ведущем столбце.
Переменная, находящаяся на пересечении ведущего столбца (k) и ведущей строки (r) называется ведущим элементом.
Определяем новое базисное решение методом Гаусса-Жордана:
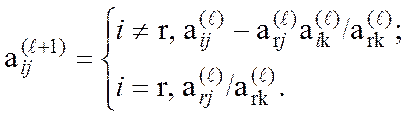
Метод искусственного базиса.
Применяется при решении задач оптимизации в случае, когда система ограничений включает в себя как ограничения в форме равенств, так и неравенств, является модификацией табличного симплексного метода.
Решение осуществляется путем ввода искусственных переменных, знак которых зависит от типа оптимизации. Они вводятся с большим отрицательным коэффициентом при поиске максимума ЦФ, и с большим положительным при решении задач минимизации.
Решение, в котором отсутствуют искусственные переменные, считается оптимальным. Если такого решения достичь невозможно, т.е. нельзя удалить из базиса все искусственные переменные, то система ограничений исходной задачи считается несовместной, а задача неразрешимой.
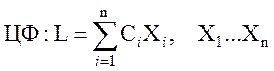
Система ограничений: 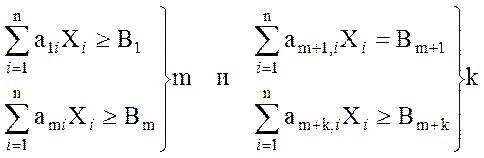
Алгоритм:
1) Система уравнений приводится к канонической форме, т.е. по средством введения вспомогательных переменных ограничения в форме неравенств приводятся к форме равенств: X1…Xn – оптимизируемые параметры, Xn+1…Xn+m – вспомогательные параметры.
2) Вводятся искусственные переменные Xn+m+1…Xn+2m+k, которые составляют начальный базис.
3) Составляем таблицу:
| Коэфф-ты ЦФ | С1 | С2 | Cn | -M | -M | ||||
| СБ | базис | X1 | X2 | Xn | Xn+1 | Xn+m | Xn+m+1 | Xn+2m+k | B |
| -M | Xn+m+1 | a11 | a12 | a1n | B1 | ||||
| -M | Xn+m+2 | a21 | a22 | a2n | B2 | ||||
| … | … | … | … | … | … | … | … | … | … |
| -M | Xn+2m+1 | am+k,1 | am+k,2 | am+k,n | Bm+k | ||||
| Искусст ЦФ | Z | Z1 | Z2 | Zn | Zn+1 | Zn+m | Zn+m+1 | Zn+2m+k |
где 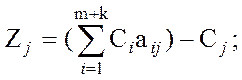
4) Из числа небазисных элементов выбираются включаемые в базис переменные по наибольшему отрицательному коэффициенту в Z строке:
min{Zj} => j=k – ведущий столбец
5) По минимальному положительному отношению соответствующего элемента в столбце B к соответствующему элементу ведущем столбце определяются исключаемые из базиса искусственные переменные, а соответствующая ей строка i=r объявляется ведущей строкой:
min(Bi/aik)>0; i=r – ведущая строка, ark – ведущий элемент
6) Находится новое базисное решение:
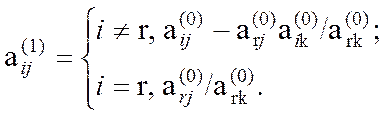
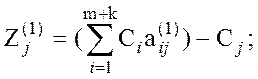
столбец, соответствующий исключаемой из базиса искусственной переменной, исключается из таблицы.
7) В базисе вместо исключенной переменной записывается включаемая.
Вычисления продолжаются до тех пор, пока из базиса не будут исключены все искусственные переменные, что соответствует оптимальному решению.
Модифицированный симплекс-метод.
В основу данного метода положены такие основы линейной алгебры, кот-ые позволяют в ходе решения задачи работать только с частью матрицы ограничений.
|A||X|≤|b|;
В процессе работы алгоритма происходит спонтанное обращение матриц ограничений по частям соотв. текущим базисным векторам. Особенности: 1) наличие двух таблиц (основной и вспомогательной); 2) порядок их заполнения; 3) специфичность расчета формул.
1-11. Учет ограничений в форме равенств при оптимизации режима ЭЭС. Метод Лагранжа. Учет ограничений в форме неравенств. Метод учета ограничений штрафными функциями.
Наиболее наглядным методом решения задачи при ограничениях в форме равенств явл-ся метод неопределенных множителей Лагранжа. Этот м-д позволяет отыскать условный экстремум непрерывной функции, явл-щейся максимумом или минимумом при выполнении дополнительных условий в форме равенств (уравнений связи).
Метод множ. Лагранжа дает возможность найти такую систем уравнений, кот-й должен удовлетворять экстремум ф-и f(x1,….,xk) на множестве N, определяемом системой уравнений gi(x) для i=1,2,…,m.
Для того чтобы найти такую точку экс-ма, харак-щейся на множ-ве Nнеким вектором Х, необходимо найти m чисел λ1,….,λm, которые вместе с вектором Х удовлетворили бы следующей системе (m+n) уравнений с (m+n) неизвестными:
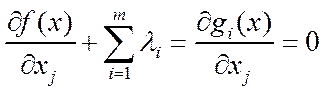

j=1,…,n; gi(x)=0; i=1,..,m.
Эти уравнения получены как условия экст-ма ф-и Лагр. 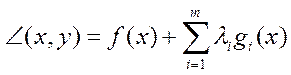 , где λ1,….,λm называются множителями Лагр.
, где λ1,….,λm называются множителями Лагр.


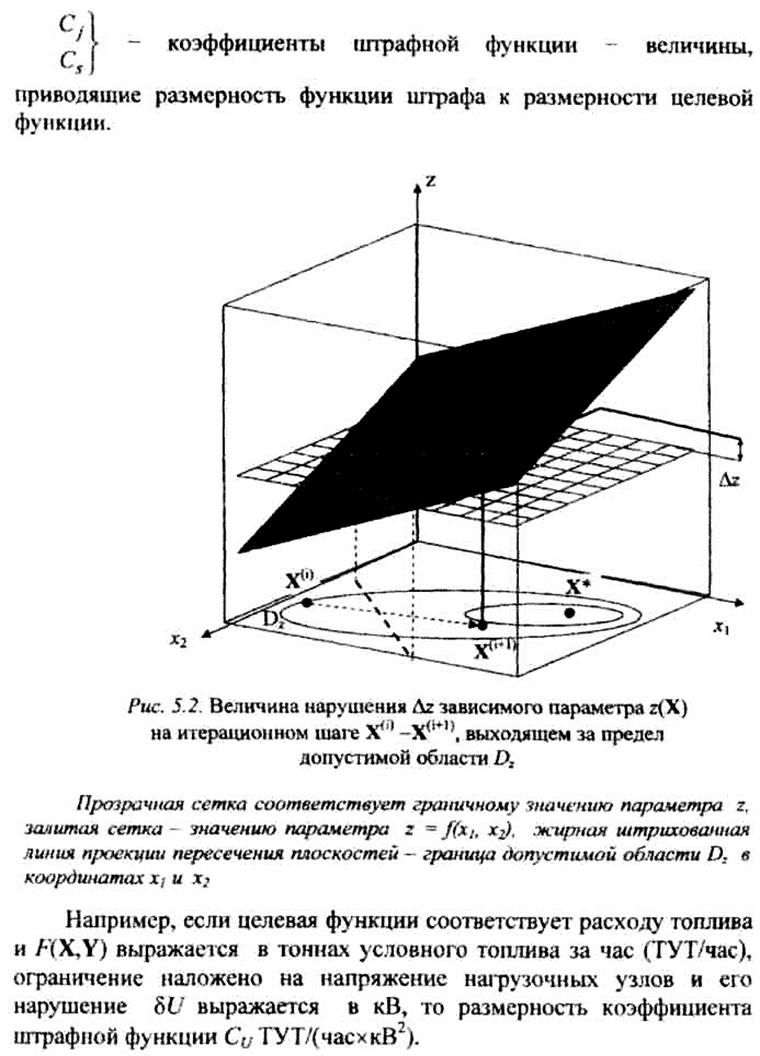
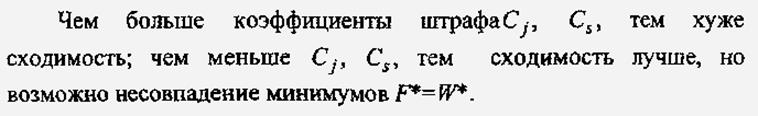
Метод штрафных ф-ий нашел широкое применение для расчета допустимых режимов.
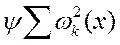 , где ωк(х)-ур-ия устан-ся режимадля к-го узла.
, где ωк(х)-ур-ия устан-ся режимадля к-го узла.
Допустимый режим-это такой р-м, для которого параметры режима xi y yi, а также ф-ции от них φi(x,y) удовлетворяют техническим ограничениям.
Для допустимых режимов должны выполняться следующие условия:
ФОРМУЛЫ
Где φL-явная вектор-ф-ия от х,у компонентами которой могут быть, например потоки мощности, потери и т.д.
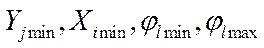 -нижние и верхние пределы для
-нижние и верхние пределы для 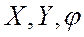 .
.
Все величины, которые должны быть в допустимых пределах наз-ся контролируемыми вел-ми (токи и потоки мощности).
Режим явл-ся допустимым если для всех j:
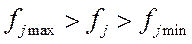 , где fj –j-ая контрол-мая величина;
, где fj –j-ая контрол-мая величина;
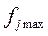 и
и 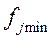 -пределы значения контр-мой величины.
-пределы значения контр-мой величины.
При использовании м-да штрафных ф-ций для расчета допустимых режимов, ф-ция 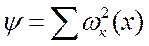 дополняется штрафной ф-цией
дополняется штрафной ф-цией
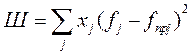 и расчет допуст. Режима соотв-ет минимуму ф-ции
и расчет допуст. Режима соотв-ет минимуму ф-ции 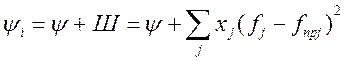 при условии сущ-ния хотя бы одного допустимого режима
при условии сущ-ния хотя бы одного допустимого режима 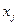 -весомый коэф-т,
-весомый коэф-т, 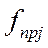 -пределы значений контрол-мой величины,
-пределы значений контрол-мой величины, 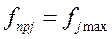 или
или 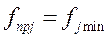 .
.
В штрафную ф-ю Ш и 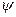 , вводят только те контрол-мые величины, для которых не выполняются ограничения
, вводят только те контрол-мые величины, для которых не выполняются ограничения 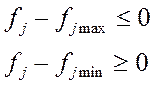 .
.
Это значит, что 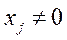 , если j ограничение нарушено и
, если j ограничение нарушено и 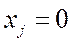 , если
, если 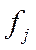 находится в допустимой области.
находится в допустимой области.
Если 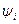 =0, то для всех
=0, то для всех 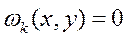 и
и 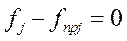 т.е. удовлетворяет УУР и все ограничения на контролируемые велечины.
т.е. удовлетворяет УУР и все ограничения на контролируемые велечины.
Дата добавления: 2015-02-10; просмотров: 1222;
