Полюса и нули

Многие динамические свойства системы (например, быстродействие, перерегулирование) определяются полюсами передаточной функции (или, что то же самое, собственными числами матрицы 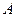модели в пространстве состояний).

Передаточную функцию можно записать как произведение передаточных функций элементарных звеньев первого и второго порядков. Таким образом, множество полюсов передаточной функции устойчивой системы составляют полюса передаточных функций двух типов простейших звеньев: апериодических и колебательных.

Апериодическое звено с передаточной функцией вида 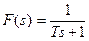имеет единственную характеристику – постоянную времени 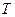. Начиная примерно с частоты[5] 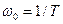, АЧХ такого звена начинает убывать, приближаясь к нулю.

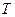Колебательное звено имеет передаточную функцию , где – постоянная времени и 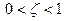. Частота 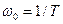называется собственной частотой (natural frequency), а параметр 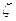– параметром затухания или коэффициентом демпфирования (damping factor). При уменьшении 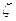импульсная и переходная функции приобретают ярко выраженный колебательный характер, а на АЧХ появляется «горб» в районе частоты 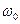. В предельном случае при 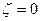колебания становятся незатухающими, а звено называется консервативным. С другой стороны при 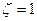корни знаменателя становятся вещественными, и звено превращается в апериодическое звено второго порядка.

Для нахождения полюсов передаточной функции f можно использовать функцию

>> p = pole ( f )

Вызов функции

>> [w0,zeta,p] = damp ( f )

позволяет найти не только полюса p, но также соответствующие им собственные частоты w0и коэффициенты демпфирования zeta в виде массивов.

Нули передаточной функции f вычисляются как

>> z = zero ( f );

Устойчивость системы не зависит от расположения нулей, но они существенно влияют на переходные процессы. Команда

>> pzmap ( f );

строит карту расположения нулей (они обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости.

[1] Черным цветом обозначается ввод пользователя, синим – ответ среды Matlab.

[2] В зарубежной литературе для одномерных систем используется сокращение SISO = Single Input Single Output.

[3] Полюса передаточной функции являются собственными числами матрицы 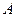. Таким образом, если у передаточной функции есть полюс в точке 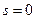, матрица 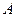будет вырожденной.

[4] Для нелинейных систем это неверно.

[5] Значение 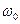возвращается функцией damp как собственная частота для вещественного полюса.