Геометрических размеров элементов, нагрузок

Одним из важнейших факторов, влияющих на несущую способность конструкции, является фактор рассеяния механических свойств, геометри- ческих размеров сечений и действующих нагрузок. Возможна оценка проч- ности по крайне неблагоприятному сочетанию всех входящих в расчет ве-личин. При небольшом количестве факторов, каждый из которых имеет небольшое рассеяние, можно добиться удовлетворительного результата. При значительном рассеянии факторов такая оценка дает низкий резуль-тат. Такие характеристики металла, как s_Т, s_В, d, КСU отличаются от об-разца к образцу даже в пределах одного листа металла. Характер наблюда-емых рассеяний приведен на диаграммах (рис. 12.1, 12.2)[10], построен-ных по результатам испытаний большого количества образцов.

По вертикали откладывается или количество появлений результата m, или частность m/n – относительная частота появления результата в до- лях единицы или в процентах; n – число испытанных образцов. Точки на диаграммах показывают появление какого - либо результата в заданном интервале изменения величины.

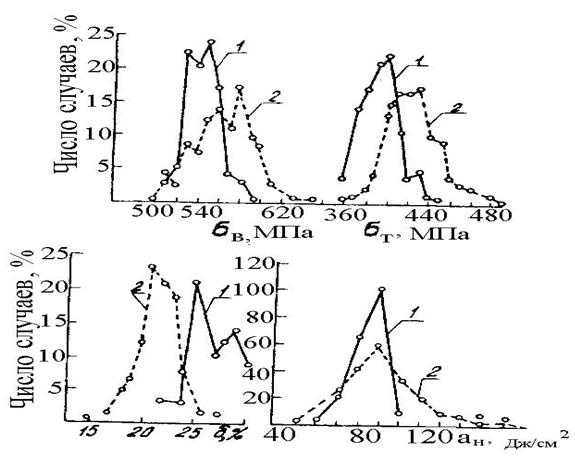
Рисунок 12.1 - Кривые распределения механических свойств

сталей 10Г2С (1) и 10Г2СД (2)

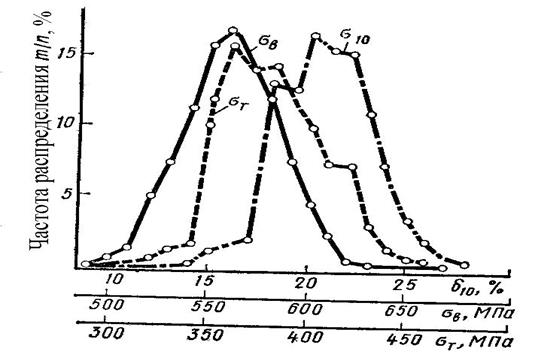
Рисунок 12.2 –Кривые распределения механических свойств стали

15ХСНД (количество случаев n = 1358)

Эмпирическая диаграмма частот называется гистограммой. Сред -ние значения случайной величины, например для временного сопротивле-ния 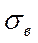, обозначаются как 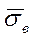и вычисляются по соответствующей формуле. Например [10]:

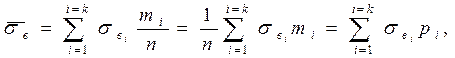(12.1)

где ­­­­­­­­­­­­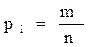– частность.

В качестве количественной характеристики распределения случай-ных величин используют также дисперсию D и среднее квадратичное отклонение S:

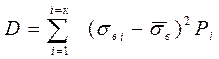; (12.2)

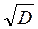S = . (12.3)

При анализе прочности сварных конструкций рассматривается вли-яние трёх групп факторов: 1) механических свойств материалов; 2) геомет-рических размеров элементов сечений, концентраторов напряжений;

3) уровня действующих нагрузок или напряжений.

Если прочности основного металла и сварного соединения имеют рассеяние (рис.12.3)[18], то оценка неравнопрочности сварного соедине- ния относительно основного металла 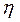= σ^/_в/σ_в 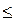1 не учитывает величи- ну рассеяния.

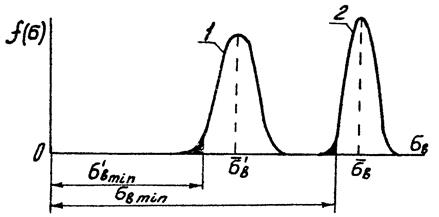
Рисунок 12.3 –Кривые рассеяния временного сопротивления сварного

соединения (1) и основного металла (2)

При предположении равной вероятности разрушения (равенство за-черченных плоскостей, рис.12.3) неравнопрочность сварного соединения относительно основного металла оценивается отношением

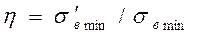, (12.4)

где σ^/_{в min} – временное сопротивление сварного соединения;

σ_{в min} – временное сопротивление основного металла.

Прочность элемента определяется свойствами металла и сечением элемента. Для соединения встык величина силы

Р = s_в F , (12.5)

где s_в – предел прочности;

F – площадь сечения элемента.

s_в, F имеют свое рассеяние.

Рассмотрим изменение P в зависимости от изменения s_в и F. Если брать средние значения силы 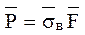, то окажется, что рассеяние ве-личин σ_{в и} F не будет влиять на вероятность разрушения. Однако дис-персия влияет на вероятность разрушения при неизменном уровне эксплу-атационной нагрузки.

D_Z = D_XD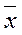_Y+ ² D_Y+ 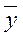² D_X. (12.6)

Рассмотрим пример изменения среднего квадратичного отклонения величины силы P в случае, есл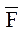и и 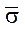имеют равные коэффициенты вариации. Пусть 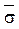_в = 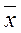= 500МПа; 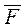= =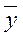100 мм²; S_X = 50; S_Y =10.

Тогда коэффициенты вариации:

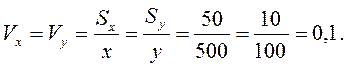
Соответственно дисперсии будут равняться:

D_x = S²_х= 2500; D_y = S²_в = 100.

Величину дисперсии D_Z силы P найдем по формуле

D_Z = D_XD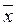_Y + ²D_Y + 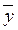²D_X = 2500 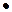100 + 500² 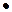100 +100² 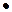2500 = =25,5 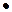10⁶Н.

Среднее квадратичное отклонение S_Z силы P равняется:

S_Z = ÖD_Z =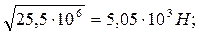

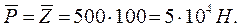
Определим коэффициент вариации V_z силы P:

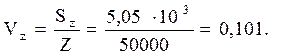
Это показывает, что коэффициент вариации возрастает, то есть воз-растает рассеяние. Закон распределения величины P зависит от законов распределения s и F. Площади поперечных сечений не могут настолько изменяться, чтобы существенным образом влиять на уровень возможного разрушения. Однако коэффициент концентрации напряжений a может оказывать сильное влияние на прочность. При малых значениях a кон-центраторы не влияют на прочность, но, начиная с определенного уровня, снижают ее по нелинейной зависимости (рис.12.4)[18], а сила определяется по формуле

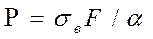. (12.7)

Рисунок 12.4 –Схематическая зависимость среднего разрушающего

напряжения σ_ср.р и средней разрушающей деформации

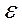_ср.р от коэффициента концентрации напряжений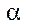

Максимальные нагрузки P_max не остаются постоянными, а могут из-меняться в некоторых пределах. Отношение средней разрушающей нагруз-ки к максимальной P_max является коэффициентом запаса разрушающей нагрузки.

Вероятностные методы в расчетах на прочность находят все боль-шее применение для оценки надежности деталей и конструкций.