Геометрическая сторона задачи
Для составления дополнительного уравнения (уравнения совместности де-
формаций) рассмотрим систему в деформированном виде.
 Балка AB повернется вокруг шарнира O, при этом точки A и B займут новые положения A1 и B1. Вследствие малости перемещений узлов конструкции действительные перемещения точек A и B по дугам окружности заменим перемещениями по вертикальным прямым AA1 и BB1. По той же причине будем считать, что углы между элементами конструкции до и после деформации остаются постоянными.
Балка AB повернется вокруг шарнира O, при этом точки A и B займут новые положения A1 и B1. Вследствие малости перемещений узлов конструкции действительные перемещения точек A и B по дугам окружности заменим перемещениями по вертикальным прямым AA1 и BB1. По той же причине будем считать, что углы между элементами конструкции до и после деформации остаются постоянными.
Из подобия треугольников OAA1 и OBB1 имеем
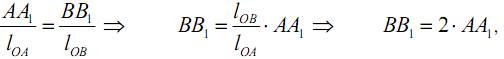
при этом заметим, что удлинение стержня AD равно перемещению AA1:

Так как 1 AD AD > , то, очевидно, что стержень AD растягивается, и его удлинение будем считать положительным .
Построим треугольник BB1B2, опустив перпендикуляр из точки B на отрезок
B1C (получим точку B2).
Удлинение стержня BC найдем из рассмотрения треугольника BB1B2, учитывая, что ∆lBC=B1B2,
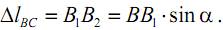
Так как 1 2 BCB C > , то, очевидно, что стержень BC растягивается, и его удлинение будем считать положительным.
Учитывая, что 1 2 1 BB A =⋅ A запишем уравнение совместности деформаций стержней AD и BC:
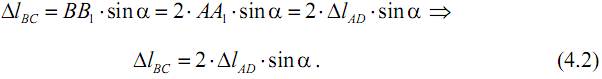
Дата добавления: 2015-02-07; просмотров: 1654;
