Раздел статика
Статика, рассматривая равновесие системы действующих на тело сил, дает правила для определения входящих в эту систему неизвестных сил (обычно это реакции связей, но определению могут подлежать и некоторые активные силы). Знание модулей и направлений всех действующих на тело сил необходимо при выполнении большинства технических расчетов, рассматриваемых в последующих разделах курса технической механики.
При рассмотрении равновесия тела наложенные на него связи следует отбросить, заменив их действие реакциями (т. е. силами действия связей на тело). Реакция гладкой опорной поверхности направлена по нормали к этой поверхности в сторону к телу. Реакция точечной опоры (ребро двугранного угла) направлена по нормали к гладкой поверхности опирающегося тела в сторону к телу. Реакция гибкой связи (трос, нить и т. п.) направлена вдоль связи в сторону от тела. Гибкая связь, перекинутая через блок, изменяет направление передаваемой силы без изменения ее модуля. Реакция жесткого прямого стержня с шарнирным закреплением концов направлена вдоль его оси в сторону от тела (если стержень нагружен растягивающей силой) или в сторону к телу (если эта сила сжимающая). Реакция шарнирно-подвижной опоры направлена по нормали к опорной поверхности шарнира. Реакцию шарнирно-неподвижной опоры принято представлять в виде двух составляющих реакций по осям координат. В заделке помимо двух составляющих реакций по осям координат возникает реактивный момент.
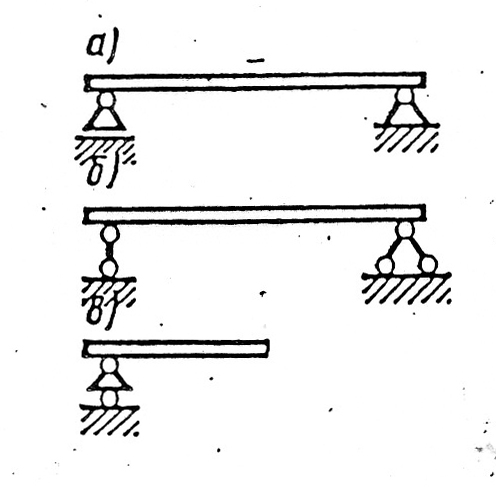
Рис. 1
Следует отметить, что в настоящем пособии условное изображение шарнирных опор соответствует требованиям действующего ГОСТа (рис.1, а); в учебниках и пособиях ранних изданий встречаются и другие изображения (рис. 1, б, в). Левая опора на каждом из рисунков подвижная, правая — неподвижна.
При решении задач следует строго соблюдать требования Международной системы единиц (СИ).
К задачам 1...10.К решению этих задач следует приступать после изучения тем «Основные понятия и аксиомы статики» и «Плоская система сходящихся сил», уяснения приведенных ниже методических указаний и разбора примеров.
В предлагаемых задачах рассматривается тело (точка), находящееся в равновесии под действием плоской системы сходящихся сил. При аналитическом методе решения применяемая система двух уравнений равновесия имеет вид 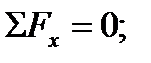
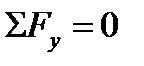 (сумма проекций сил системы на каждую из координатных осей равна нулю). В учебной литературе применяется и другая форма записи этих же уравнений:
(сумма проекций сил системы на каждую из координатных осей равна нулю). В учебной литературе применяется и другая форма записи этих же уравнений: 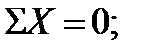
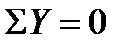 . Напоминаем, что проекция силы на ось равна произведению модуля силы на косинус ее острого угла с осью. Знак проекции (рис. 2) определяется совпадением направлений проекции и оси ( направление проекции — от
. Напоминаем, что проекция силы на ось равна произведению модуля силы на косинус ее острого угла с осью. Знак проекции (рис. 2) определяется совпадением направлений проекции и оси ( направление проекции — от 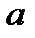 к
к 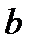 ).
).
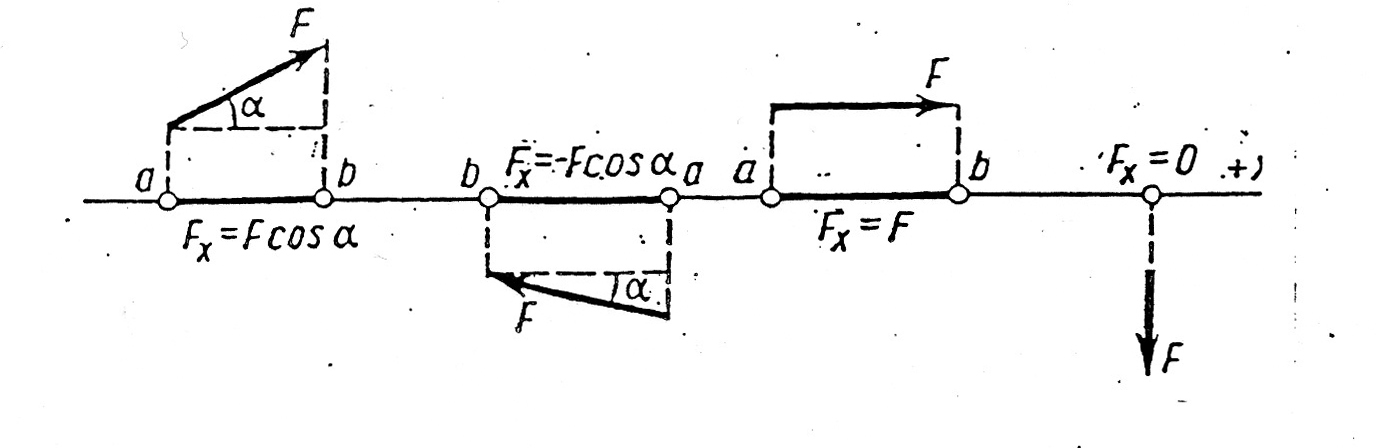
Рис. 2
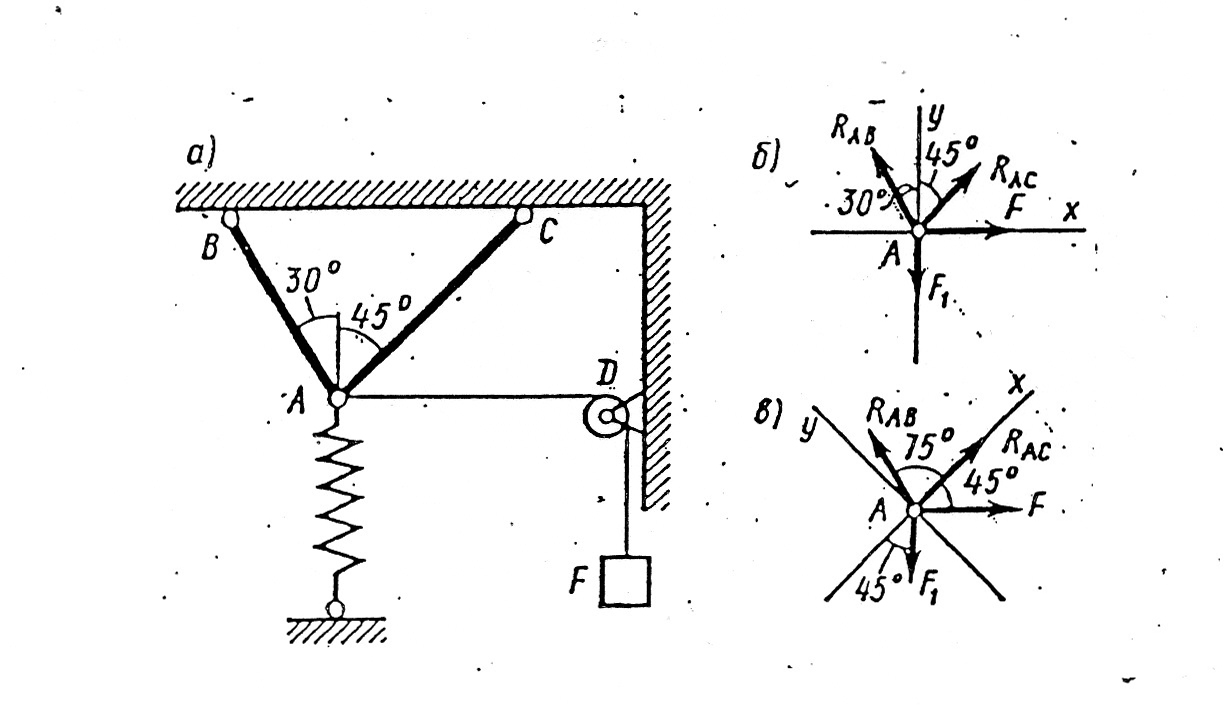
Рис. 3
Пример 1 (рис.3, а). Определить силы, нагружающие стержни АВ и АС кронштейна, удерживающего в равновесии груз 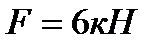 и растянутую пружину, сила упругости которой
и растянутую пружину, сила упругости которой 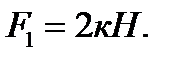 Весом частей конструкции, а также трением на блоке пренебречь.
Весом частей конструкции, а также трением на блоке пренебречь.
Решение. Задачу решаем аналитическим методом. Рассматриваем равновесие точки схода А. К ней приложены заданные активные силы — сила натяжения троса АD, равная весу груза F, и сила упругости пружины F1. Так как и трос, и пружина растянуты, то эти силы направлены от точки А. Рассматривая точку А как свободную, отбрасываем связи (стержни АВ и АС), заменяя их действие реакциями RAB и RAС . Реакция стержней направляем от точки А, так как предварительно полагаем стержни растянутыми (действительные направления реакций стержней в начале решения неизвестны). Если наше предположение окажется неверным, то искомая реакция стержня получится в ответе со знаком минус; это говорит о том, что стержень сжат и истинное направление реакции — к точке А. Полученная расчетная схема изображена на рис. 3, б.
Принимаем обычное вертикально-горизонтальное направление координатных осей. Для полученной плоской системы сходящихся сил составляем два уравнения равновесия:
1) 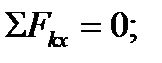
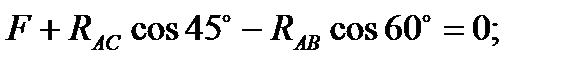
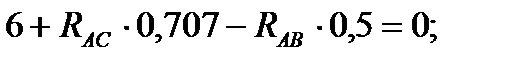
2) 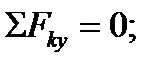
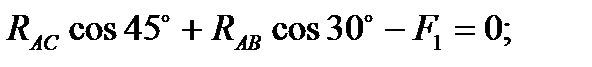
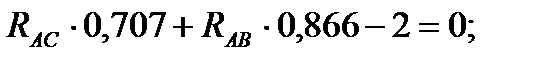
Решая полученную систему уравнений, находим 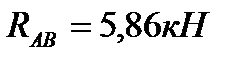 и
и 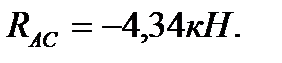 Искомые силы, нагружающие стержни, по модулю равны найденным реакциям стержней, а по направлению противоположны им. Замечаем, что в соответствии с изложенным правилом стержень АВ оказался растянутым, а стержень АС — сжатым.
Искомые силы, нагружающие стержни, по модулю равны найденным реакциям стержней, а по направлению противоположны им. Замечаем, что в соответствии с изложенным правилом стержень АВ оказался растянутым, а стержень АС — сжатым.
Следует отметить, что каждое из полученных уравнений равновесия содержало оба неизвестных, чего можно было избежать, направив координатные оси по-другому — совместив одну из осей с неизвестной силой (рис. 3, в). При этом в уравнении равновесия для другой оси окажется лишь одно неизвестное:
1) 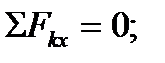
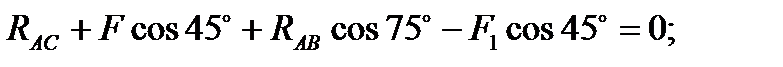
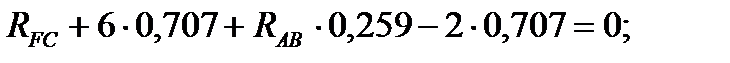
2) 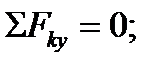
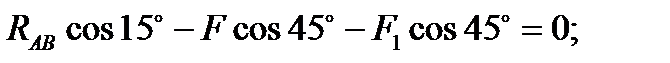
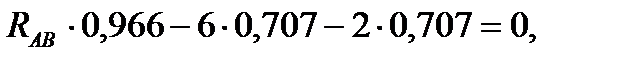
откуда 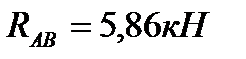 и
и 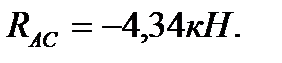
Для проверки правильности решения составляем проверочное уравнение равновесия — уравнение проекций сил на любую ось, кроме уже использованных в решении. Продолжая к примеру первый вариант решения (по рис. 3,б), возьмем в качестве такой оси направление 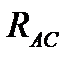 (можно было бы и
(можно было бы и 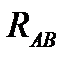 ) и обозначим эту ось
) и обозначим эту ось 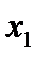 . Тогда получим
. Тогда получим
3) 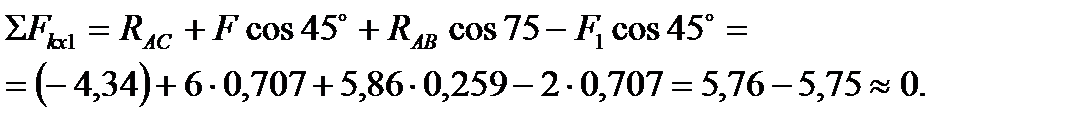
Полученное небольшое расхождение в третьем знаке допустимо, так как объясняется погрешностью счета.
Проверяем правильность полученных результатов, решая задачу графически (рис. 3, г.). Полученная система сил (рис. 1, б) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.
Строим силовой многоугольник в следующем порядке (рис. 3, г) в выбранном масштабе (например, 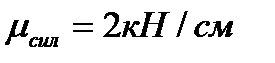 ) откладываем заданную силу
) откладываем заданную силу 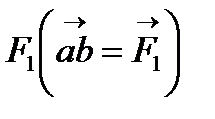 , затем из точки b под углом 900 к горизонту откладываем силу
, затем из точки b под углом 900 к горизонту откладываем силу 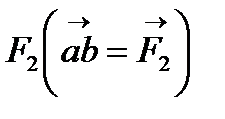 , далее из точек а и с проводим прямые, параллельные положениям стержней АВ и АС. Эти прямые пересекаются в точке d и в результате построения образуются замкнутый многоугольник abcd, в котором сторона
, далее из точек а и с проводим прямые, параллельные положениям стержней АВ и АС. Эти прямые пересекаются в точке d и в результате построения образуются замкнутый многоугольник abcd, в котором сторона 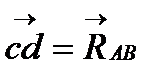 , а сторона
, а сторона 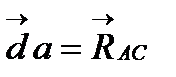 . Измерив длины этих сторон (в см) и умножив на масштаб построения
. Измерив длины этих сторон (в см) и умножив на масштаб построения 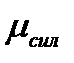 , получаем значения реакций стержней:
, получаем значения реакций стержней:
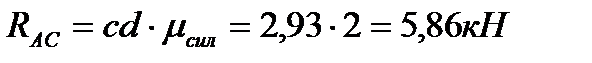 и
и 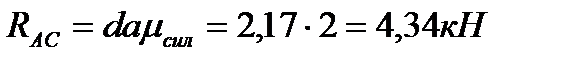
Графическое решение подтверждает правильность первого решения.
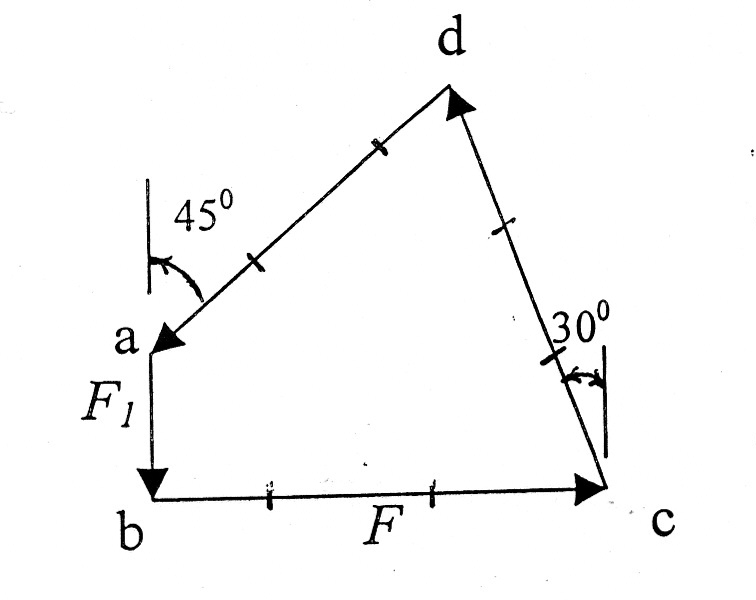
Рис. 3 г.
Пример 2 (рис. 4, а). Для заданной двухопорной балки определить опорные реакции.
Решение. Рассматриваем равновесие балки АD. К ней приложены заданные активные силы F1 и F2 и момент М. Рассматривая тело АD как свободное, отбрасываем связи (шарнирные опоры А и В), заменяя их действие реакциями. Реакция RA шарнирно-подвижной опоры А направлена по нормали к опорной поверхности. Для шарнирно-неподвижной опоры В показываем составляющие реакции Rx и Ry по осям координат. Расчетная схема изображена на рис. 4, б.
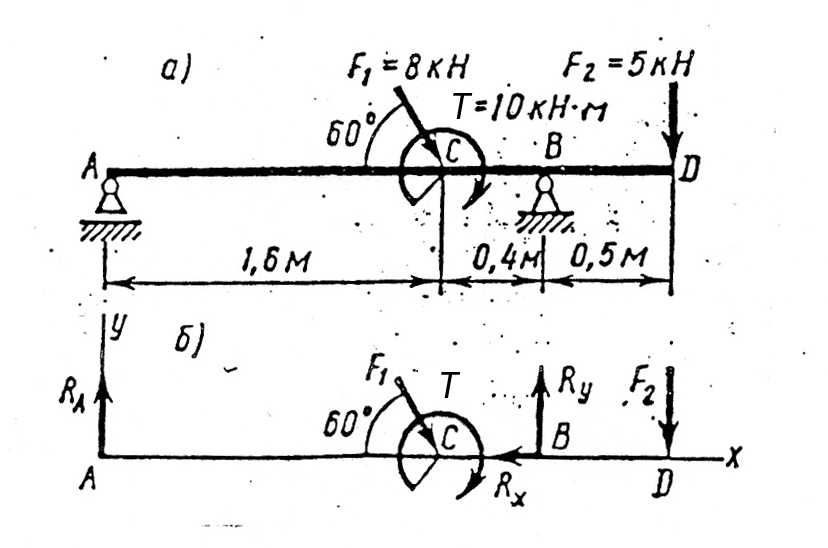
Рис. 4
Для полученной плоской системы произвольно расположенных сил составляем три уравнения равновесия, выбрав в качестве центра моментов точки А и В (точки пересечения двух неизвестных сил):
1) 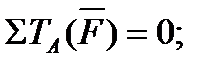
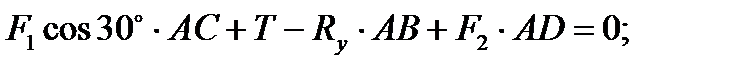
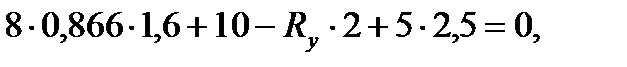 отсюда
отсюда 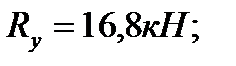
2) 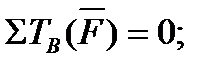
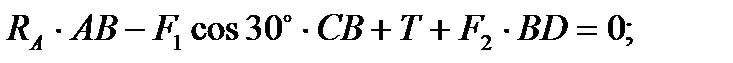
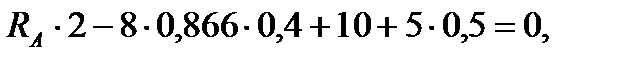 отсюда
отсюда 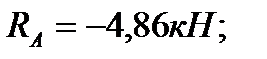
3) 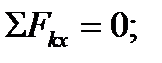
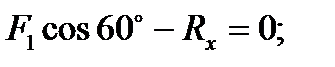
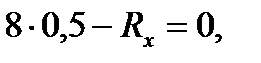 отсюда
отсюда 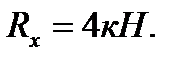
Составляем проверочное уравнение равновесия:
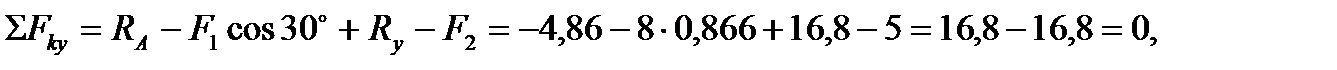
следовательно, реакции определены верно. Реакция RAполучилась отрицательной; значит, ее действительное направление противоположно предварительно выбранному.
Примененная система уравнений равновесия наиболее целесообразна при рассмотрении равновесия любых двухопорных балок.
Приступая ко второй контрольной работе, в которой выполняются в основном расчеты деталей и конструкций на прочность, прежде всего необходимо повторить из раздела «Статика» методику определения реакций связей стержневых конструкций и балок.
Раздел сопротивление материалов
В сопротивлении материалов выполняются в основном расчеты деталей и конструкций на прочность, прежде всего необходимо повторить из раздела «Статика» методику определения реакций связей стержневых конструкций и балок. Затем, изучив соответствующий учебный материал, следует получить четкое представление о методе сечений для определения внутренних силовых факторов, о видах нагружения бруса, напряжениях, условии прочности и видах расчетов на прочность. В противном случае успешное решение задач контрольной работы невозможно.
Напомним общий для всех видов нагружения бруса порядок выполнения расчета на прочность:
1. С помощью метода сечений по виду и расположению нагрузок, к которым относятся как активные, так и реактивные внешние силы и моменты, устанавливают вид внутренних силовых факторов, возникающих в поперечных сечениях бруса, и делают вывод о виде нагружения бруса.
В тех случаях, когда плоскости действия внешних моментов совпадают с координатными плоскостями, а линии действия внешних сил — с координатными осями, установление вида нагружения бруса не вызывает особых затруднений. Напоминаем, что координатные оси сечения совмещены с его главными центральными осями.
2. С помощью метода сечений определяют значение и знак внутренних силовых факторов во всех сечениях по длине бруса, строят их эпюры и отыскивают опасное сечение бруса.
Внутренний силовой фактор (ВСФ) в произвольном поперечном сечении бруса численно равен алгебраической сумме соответствующих нагрузок (Н), действующих на оставленную для рассмотрения часть бруса: 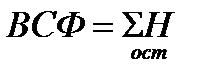 Установленное в статике для сил и моментов правило знаков при определении ВСФ неприменимо. Для каждого вида ВСФ устанавливается собственное правило знаков, отражающее обычно характер деформирования бруса. Не следует забывать, что при построении эпюры любого ВСФ должно соблюдаться следующее общее правило, вытекающее из метода сечений: ВСФ в сечении, в котором приложена соответствующая сосредоточенная нагрузка, изменяется «скачком» на значение этой нагрузки.
Установленное в статике для сил и моментов правило знаков при определении ВСФ неприменимо. Для каждого вида ВСФ устанавливается собственное правило знаков, отражающее обычно характер деформирования бруса. Не следует забывать, что при построении эпюры любого ВСФ должно соблюдаться следующее общее правило, вытекающее из метода сечений: ВСФ в сечении, в котором приложена соответствующая сосредоточенная нагрузка, изменяется «скачком» на значение этой нагрузки.
3. По виду ВСФ устанавливают вид напряжения, возникающего в точках опасного поперечного сечения, закон его распределения по сечению и вид геометрической - характеристики прочности сечения (ГХП).
Расчетное напряжение (максимальное напряжение в опасной точке опасного сечения бруса) определяют как отношение ВСФ/ГХП.
В случае равномерного распределения напряжений по поперечному сечению в качестве ГХП применяется площадь сечения А (форма сечения значения не имеет), в случае неравномерного распределения напряжений — момент сопротивления 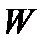 (характеризует как площадь, так и форму сечения).
(характеризует как площадь, так и форму сечения).
4. Из условия прочности бруса определяют требуемое значение искомой величины. Условием прочности при расчете по допускаемому напряжению называют неравенство вида 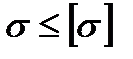 или
или 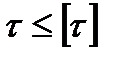 , где
, где 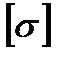 и
и 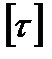 —допускаемое напряжение, зависящее от механических характеристик материала бруса и принятого коэффициента запаса прочности;
—допускаемое напряжение, зависящее от механических характеристик материала бруса и принятого коэффициента запаса прочности;  и
и 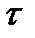 — расчетное напряжение.
— расчетное напряжение.
При решении задач следует строго соблюдать требования Международной системы единиц (СИ). Для механического напряжения и модуля упругости вместо системной единицы Па (паскаль) в настоящем пособии принята внесистемная единица Н/мм2. Числовые значения упомянутых величин, выраженные в МПа и Н/мм2, совпадают.
К задачам 21...30. К решению этих задач следует приступать после изучения темы «Кручение», уяснения приведенных ниже методических указаний и разбора примера.
Кручениемназывают такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент 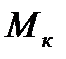 .
.
Крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних моментов, действующих на оставленную часть 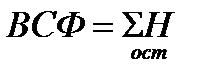 (имеется в виду, что плоскости действия всех внешних моментов перпендикулярны продольной оси бруса).
(имеется в виду, что плоскости действия всех внешних моментов перпендикулярны продольной оси бруса).
Установим следующее правило знаков: внешний момент, направленный по ходу часовой стрелки (при взгляде со стороны проведенного сечения), считается положительным (т. е. дает положительный крутящий момент); в противном случае внешний момент отрицателен (рис.5).
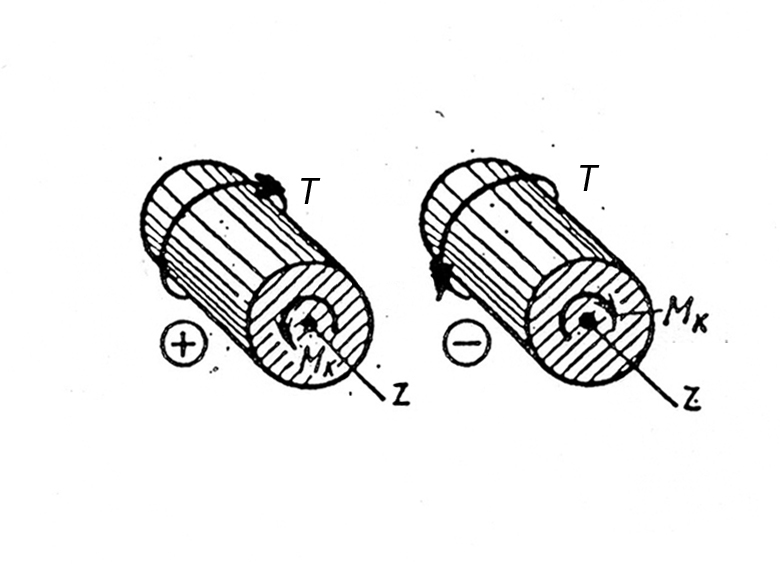
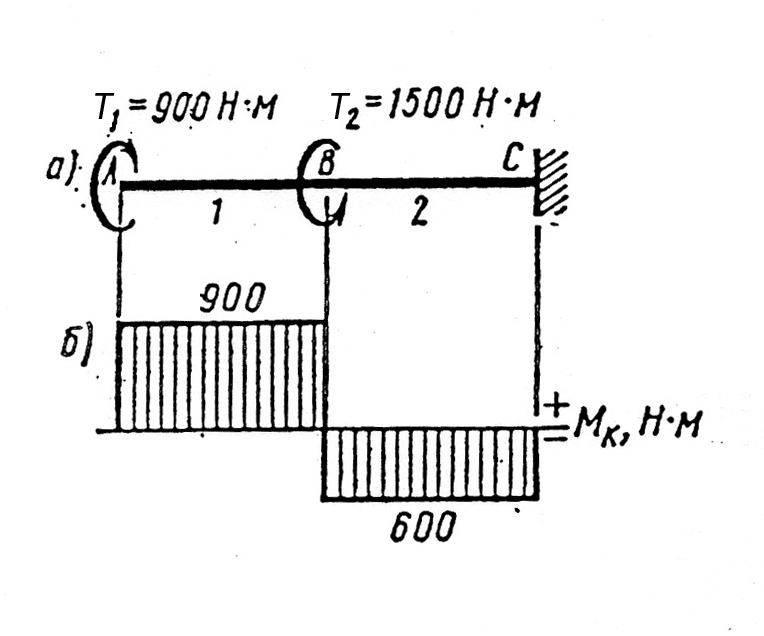
Рис. 5 Рис. 6
Пример 3 (рис.6, а). Для заданного бруса подобрать размеры сечения на каждом из его участков в двух вариантах: а) круг; б) кольцо с заданным отношением 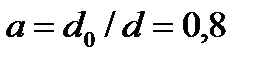 внутреннего и наружного диаметров. Сравнить массы брусьев по обоим расчетным вариантам. Для материала бруса (сталь Ст3) принять допускаемое напряжение при кручении
внутреннего и наружного диаметров. Сравнить массы брусьев по обоим расчетным вариантам. Для материала бруса (сталь Ст3) принять допускаемое напряжение при кручении 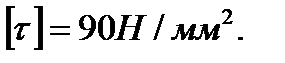
Решение. В заданном брусе два участка: 1 и 2. Границами участков являются сечения, в которых приложены внешние (скручивающие) моменты. Так как моменты, нагружающие брус, действуют в плоскостях, перпендикулярных его продольной оси, то в поперечных сечениях возникает лишь один внутренний силовой фактор — крутящий момент 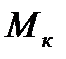 т. е. имеет место кручение бруса.
т. е. имеет место кручение бруса.
При определении крутящего момента применяем метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать правую закрепленную часть бруса и оставлять для рассмотрения левую часть. На участке 1 крутящий момент постоянен и равен 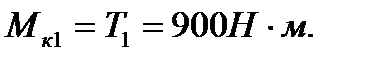 На участке 2крутящий момент также постоянен и равен
На участке 2крутящий момент также постоянен и равен 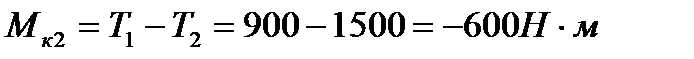 (знак крутящего момента физического смысла не имеет). Построенная эпюра крутящих моментов
(знак крутящего момента физического смысла не имеет). Построенная эпюра крутящих моментов 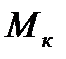 показана на рис. 6, б(построение эпюры крутящих моментов принципиально ничем не отличается от построения эпюры продольных сил).
показана на рис. 6, б(построение эпюры крутящих моментов принципиально ничем не отличается от построения эпюры продольных сил).
Определим размеры поперечного сечения бруса для каждого участка в отдельности. Для этого используем условие прочности при кручении 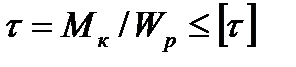 , где полярный момент сопротивления
, где полярный момент сопротивления 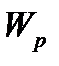 является геометрической характеристикой прочности поперечного сечения и для круга диаметра
является геометрической характеристикой прочности поперечного сечения и для круга диаметра 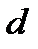 . выражается формулой
. выражается формулой 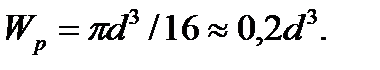 , а для кольца — формулой
, а для кольца — формулой
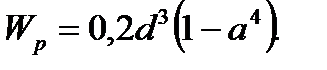
Для участка 1: 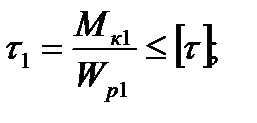
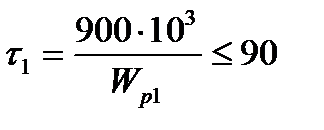 , отсюда требуемый
, отсюда требуемый
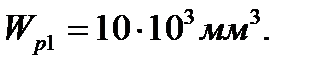
1.Для круглого сечения приравниваем 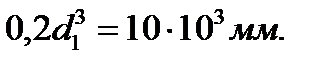 и находим
и находим 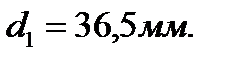 Принимаем
Принимаем 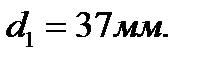
2.Для кольцевого сечения 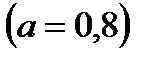 приравниваем
приравниваем 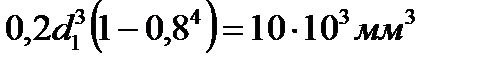 и находим
и находим 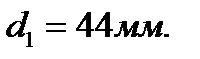 Тогда
Тогда 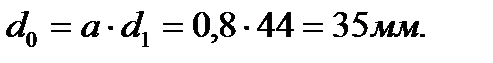
3.Для участка 2:
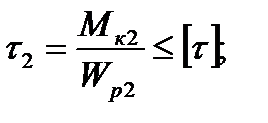
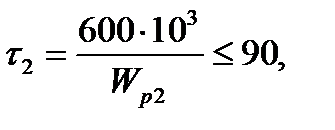 отсюда требуемый
отсюда требуемый
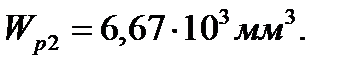
1.Для круглого сечения 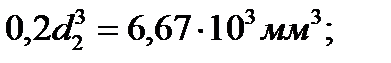
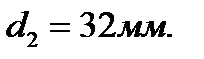
2.Для кольцевого сечения 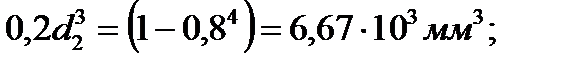
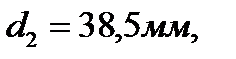 принимаем
принимаем 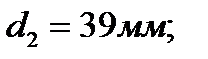
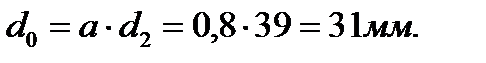
Здесь взятые по абсолютной величине крутящие моменты 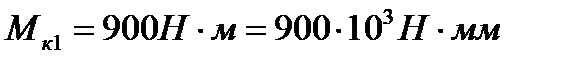 и
и 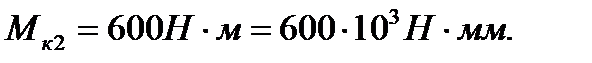
Теперь сравним затраты материала по обоим расчетным вариантам к примеру для участка 1. Отношение масс брусьев одинаковой длины равно отношению площадей их сечений. Площадь круглого сечения 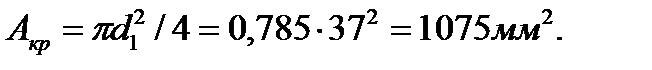 Площадь кольцевого сечения
Площадь кольцевого сечения 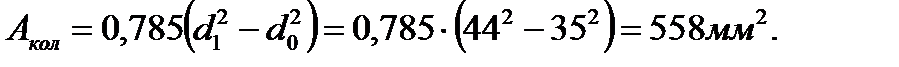
Тогда 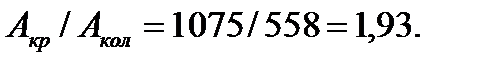 Следовательно, брус круглого сечения тяжелее кольцевого примерно в 2 раза.
Следовательно, брус круглого сечения тяжелее кольцевого примерно в 2 раза.
К задачам 31...40. К решению этих задач следует приступать после тщательного изучения темы «Изгиб», уяснения приведенных ниже методических указаний и разбора примеров.
Чистым изгибом называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — изгибающий момент Мx. В большинстве случаев одновременно с изгибающим моментом возникает и другой внутренний силовой фактор — поперечная сила Q; такой изгиб называют поперечным.
Изгибающий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на оставленную часть, относительно центра тяжести сечения: 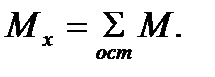 Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на оставленную часть:
Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на оставленную часть: 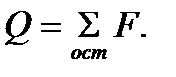 Здесь имеется в виду, что все внешние силы и моменты действуют, в главной продольной плоскости бруса, причем силы расположены перпендикулярно продольной оси “Z”
Здесь имеется в виду, что все внешние силы и моменты действуют, в главной продольной плоскости бруса, причем силы расположены перпендикулярно продольной оси “Z”
При чистом изгибе в поперечных сечениях возникают нормальные напряжения  , а при поперечном изгибе, кроме того, и касательные напряжения
, а при поперечном изгибе, кроме того, и касательные напряжения 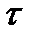 . Однако в подавляющем большинстве случаев влияние
. Однако в подавляющем большинстве случаев влияние 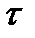 при расчете на прочность не учитывается, поэтому отпадает необходимость как в определении поперечных сил Q, так и в построении их эпюры.
при расчете на прочность не учитывается, поэтому отпадает необходимость как в определении поперечных сил Q, так и в построении их эпюры.
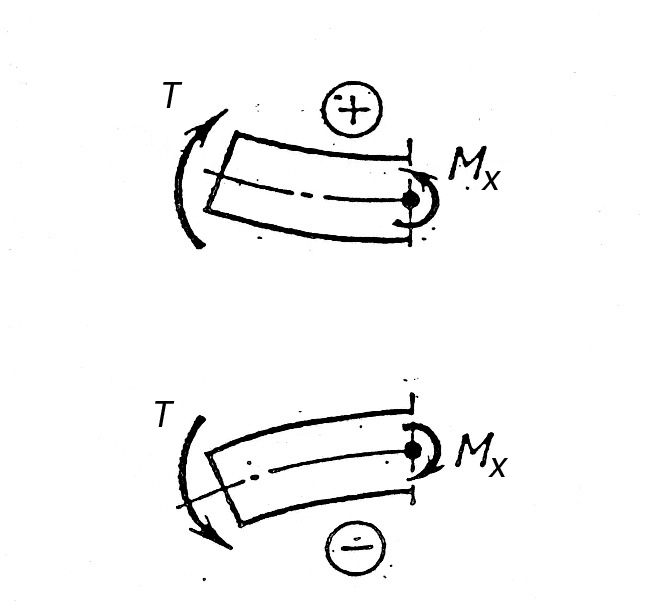
Рис. 7
Установим следующее правило знаков для изгибающего момента: момент внешней силы или пары, изгибающий мысленно закрепленную в сечении оставленную часть бруса выпуклостью вниз, считается положительным (т. е. дает положительный изгибающий момент); в противном случае момент внешней силы или пары отрицателен (рис. 7).
Поясним изложенное на примере (рис. 8). В сечении 1 - 1 изгибающий момент 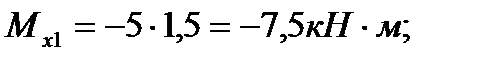 в сечении 2 - 2изгибающий момент
в сечении 2 - 2изгибающий момент 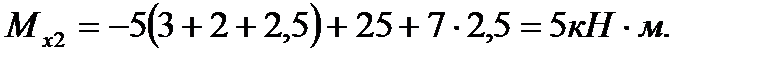 При этом мы отбрасывали правую от сечения часть балки (брус, испытывающий изгиб, называют балкой) и оставляли для рассмотрения левую часть, т. е. вели расчет «с левого конца балки». Легко убедиться, что при расчете с правого конца балки получим те же результаты. Для реальной, закрепленной одним концом балки расчет целесообразно вести со свободного конца (чтобы избежать определения опорных реакций); в случае двухопорной, балки решение задачи приходится начинать с определения опорных реакций.
При этом мы отбрасывали правую от сечения часть балки (брус, испытывающий изгиб, называют балкой) и оставляли для рассмотрения левую часть, т. е. вели расчет «с левого конца балки». Легко убедиться, что при расчете с правого конца балки получим те же результаты. Для реальной, закрепленной одним концом балки расчет целесообразно вести со свободного конца (чтобы избежать определения опорных реакций); в случае двухопорной, балки решение задачи приходится начинать с определения опорных реакций.
Балки выполняют постоянного по длине поперечного сечения, поэтому его размеры подбирают только для опасного сечения — сечения с максимальным по абсолютному значению изгибающим моментом.
Пример 4 (рис. 9, а). Для заданной консольной балки подобрать размеры сечения в двух вариантах: а) двутавр; б) прямоугольник с заданным отношением 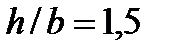 высоты и ширины. Сравнить массы балок по обоим расчетным вариантам. Для материала балки (сталь СтЗ) принять допускаемое напряжение при изгибе
высоты и ширины. Сравнить массы балок по обоим расчетным вариантам. Для материала балки (сталь СтЗ) принять допускаемое напряжение при изгибе 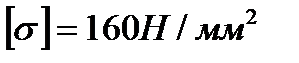 .
.
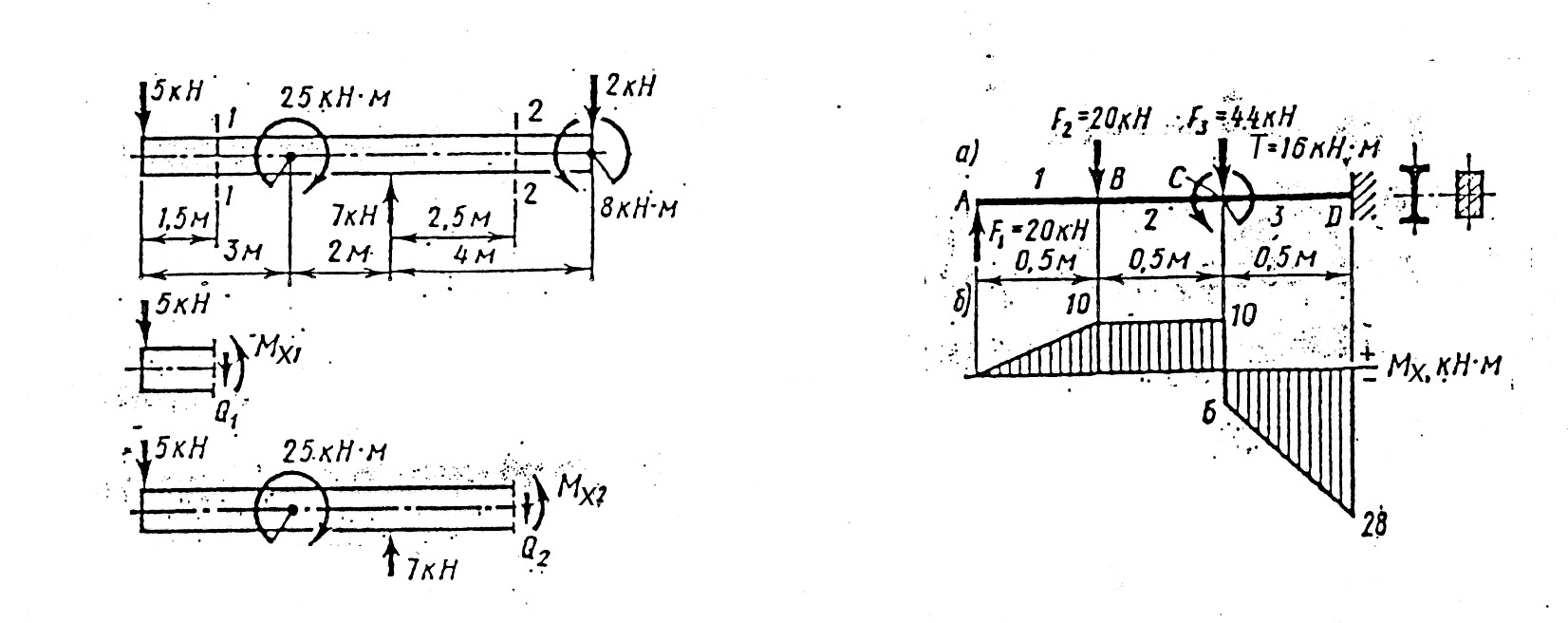 Рис. 8 Рис.9
Рис. 8 Рис.9
Решение. В заданном брусе три участка: 1, 2 и 3. Границами участков являются сечения, в которых приложены внешние силы и моменты. Так как силы и моменты, нагружающие брус, действуют в продольной плоскости, совпадающей с плоскостью симметрии бруса, то в поперечных сечениях возникает два внутренних силовых фактора — изгибающий момент Ми и поперечная сила Q, т. е. брус испытывает изгиб.
Для определения изгибающего момента применяем метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать правую закрепленную часть балки и оставлять для рассмотрения левую часть. Эпюру изгибающих моментов строим по характерным точкам, т. е. вычисляем Ми,в характерных сечениях А, В, С и D. В сечении А изгибающий момент МиА=0, так как относительно точки А внешняя сила F1 момента не создает (плечо силы равно нулю). В сечении В изгибающий момент 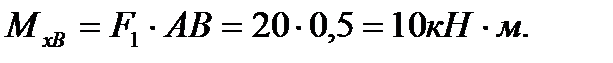 В сечении С участка 2 (т. е. в сечении, бесконечно близком к сечению С слева) изгибающий момент
В сечении С участка 2 (т. е. в сечении, бесконечно близком к сечению С слева) изгибающий момент 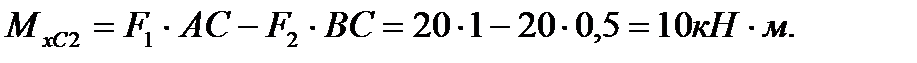 В сечении С участка 3 (т. е. в сечении, бесконечно близком к сечению С справа) изгибающий момент
В сечении С участка 3 (т. е. в сечении, бесконечно близком к сечению С справа) изгибающий момент 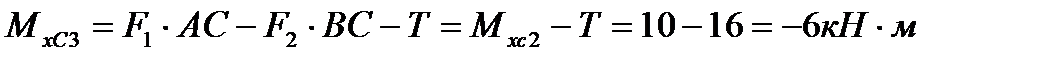 (т.е. в сечении С изгибающий момент изменился «скачком» на значение приложенного здесь внешнего момента М). В сечении Dизгибающий момент
(т.е. в сечении С изгибающий момент изменился «скачком» на значение приложенного здесь внешнего момента М). В сечении Dизгибающий момент 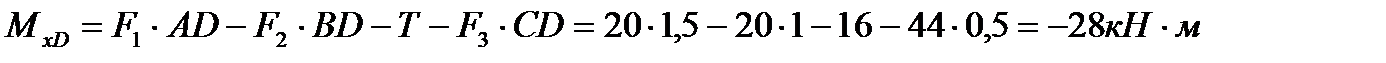 .
.
Нанося полученные характерные точки на график и соединяя их прямыми линиями, получаем эпюру изгибающих моментов Мx (рис. 9,б).
Определяем размеры поперечного сечения балки, для чего используем условие прочности при изгибе 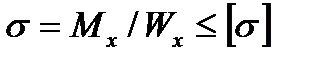 , где осевой момент сопротивления
, где осевой момент сопротивления 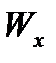 является геометрической характеристикой прочности поперечного сечения, а Мx — взятый по абсолютному значению максимальный изгибающий момент.
является геометрической характеристикой прочности поперечного сечения, а Мx — взятый по абсолютному значению максимальный изгибающий момент.
В нашем случае в опасном сечении (сечение D) 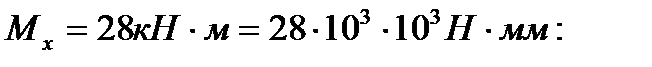
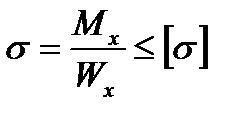 ;
; 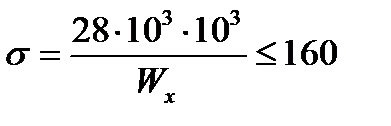 ,
,
отсюда требуемый момент сопротивления 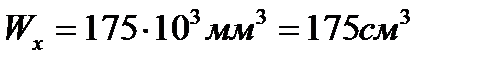 .
.
Подбираем сечение балки в двух вариантах.
1. Сечение — двутавр. По таблице прокатной стали- ГОСТ 8239—72 выбираем двутавр № 20, для которого 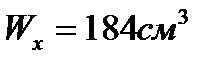 и площадь сечения А — 26,8 см2.
и площадь сечения А — 26,8 см2.
2. Сечение — прямоугольник с заданным отношением 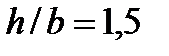 высоты и ширины. Для прямоугольника момент сопротивления
высоты и ширины. Для прямоугольника момент сопротивления 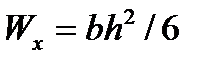 . В нашем случае
. В нашем случае 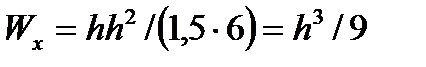 . Приравнивая
. Приравнивая 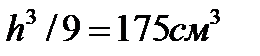 , находим
, находим 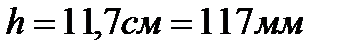 и
и 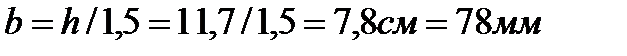 .
.
Отношение масс балок одинаковой длины равно отношению площадей сечений 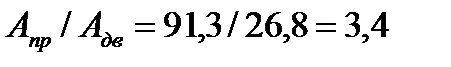 . Следовательно, балка прямоугольного сечения тяжелее двутавровой в 3,4 раза.
. Следовательно, балка прямоугольного сечения тяжелее двутавровой в 3,4 раза.
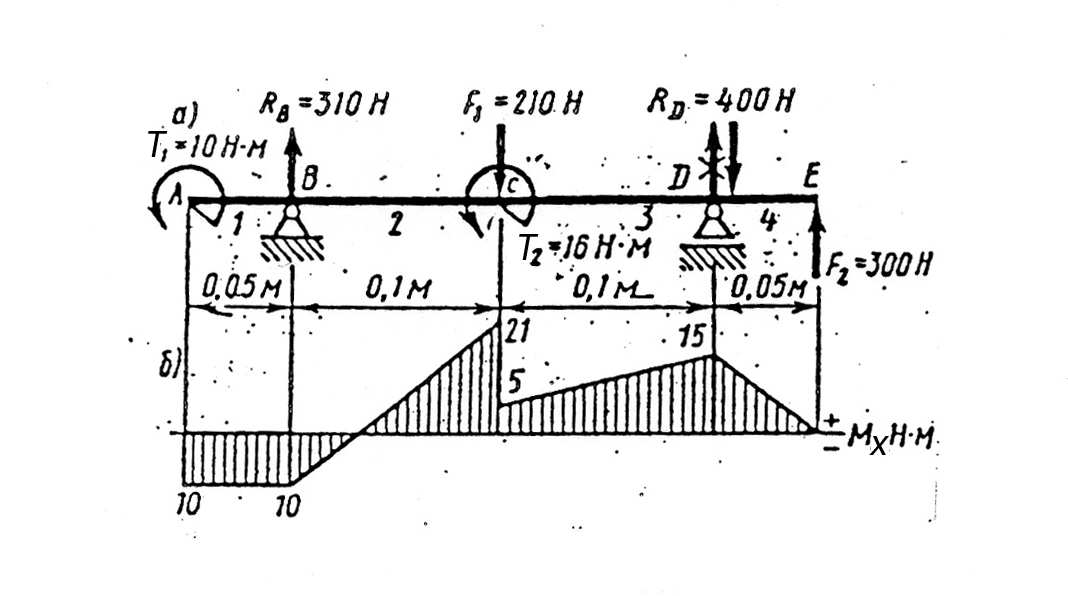
Рис. 10
Пример 5 (рис.10, а). Подобрать размеры квадратного сечения заданной двухопорной балки. Для материала балки (сталь Ст3) с учетом повышенных требований к ее жесткости принять 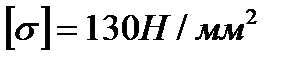 .
.
Решение. В заданном брусе четыре участка: 1, 2, 3и 4. Имеет место изгиб бруса.
В отличие от рассмотренной в предыдущем примере консольной (т. е. одноопорной) балки расчет двухопорной балки следует начать с определения реакций 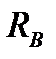 и
и 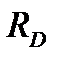 шарнирных опор (горизонтальная реакция шарнирно-неподвижной опоры В, очевидно, равна нулю). Полагая обе реакции направленными вверх, составляем два уравнения равновесия, выбрав в качестве центра моментов точки В и D (более подробно о составлении уравнений равновесия см. Методические указания к выполнению первой контрольной работы — раздел «Статика»):
шарнирных опор (горизонтальная реакция шарнирно-неподвижной опоры В, очевидно, равна нулю). Полагая обе реакции направленными вверх, составляем два уравнения равновесия, выбрав в качестве центра моментов точки В и D (более подробно о составлении уравнений равновесия см. Методические указания к выполнению первой контрольной работы — раздел «Статика»):
1) 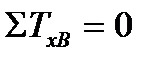 ;
; 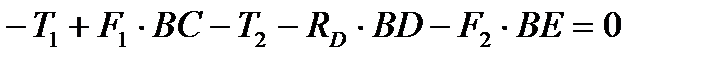 ;
;
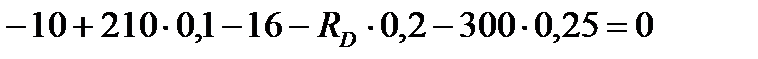 , отсюда
, отсюда 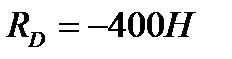 ;
;
2) 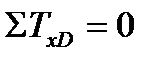 ;
; 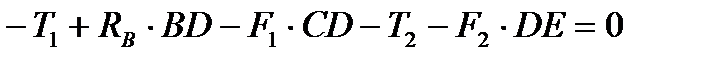 ;
;
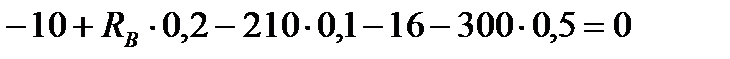 , отсюда
, отсюда 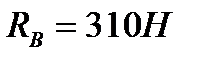 .
.
Составляем проверочное уравнение равновесия: 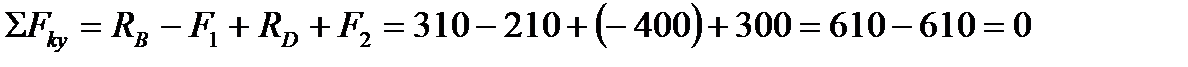 ; следовательно, реакции опор определены верно. Реакция
; следовательно, реакции опор определены верно. Реакция 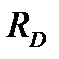 получилась отрицательной, т. е. направлена не вверх, а вниз (что и показываем на чертеже, перечеркивая предварительно выбранное направление и принимая
получилась отрицательной, т. е. направлена не вверх, а вниз (что и показываем на чертеже, перечеркивая предварительно выбранное направление и принимая 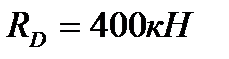 ). Найденные значения
). Найденные значения 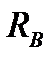 и
и 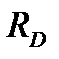 проставляем на чертеже.
проставляем на чертеже.
Для определения изгибающего момента применяем метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать правую часть балки и оставлять для рассмотрения левую часть, т. е. строим эпюру слева направо (с равным успехом можно было принять порядок построения справа налево). Эпюру изгибающих моментов строим по характерным толчкам, т. е. вычисляем Ми в характерных сечениях А, В, С, D и Е. В сечениях А и В, равно как и в любом другом сечении участка 1, изгибающий момент постоянен и равен 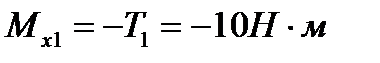 . В сечении С участка 2(т. е. в сечении, бесконечно близком к сечению С слева) изгибающий момент
. В сечении С участка 2(т. е. в сечении, бесконечно близком к сечению С слева) изгибающий момент 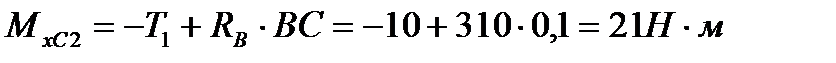 . В сечении С участка 3(т. е. в сечении, бесконечно близком к сечению С справа) изгибающий момент
. В сечении С участка 3(т. е. в сечении, бесконечно близком к сечению С справа) изгибающий момент 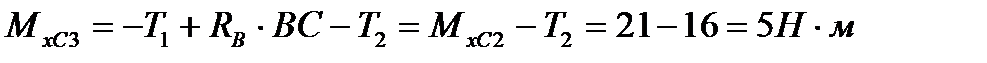 . (т. е. в сечении С изгибающий момент изменился «скачком» на значение приложенного здесь внешнего момента
. (т. е. в сечении С изгибающий момент изменился «скачком» на значение приложенного здесь внешнего момента 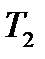 ).
).
Для упрощения расчетов дальнейшие вычисления 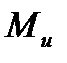 целесообразно проводить справа налево, т. е. отбрасывая левую часть балки и оставляя для рассмотрения правую часть. В сечении D изгибающий момент
целесообразно проводить справа налево, т. е. отбрасывая левую часть балки и оставляя для рассмотрения правую часть. В сечении D изгибающий момент 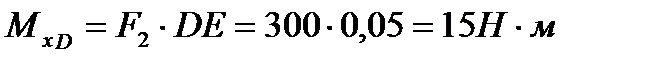 . В сечении E изгибающий момент
. В сечении E изгибающий момент  так как относительно точки Е внешняя сила F2 момента не создает (плечо силы равно нулю). Нанося полученные характерные точки на график и соединяя их прямыми линиями, получаем эпюру изгибающих моментов
так как относительно точки Е внешняя сила F2 момента не создает (плечо силы равно нулю). Нанося полученные характерные точки на график и соединяя их прямыми линиями, получаем эпюру изгибающих моментов 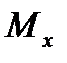 (рис. 10,б).
(рис. 10,б).
Заметим, что при построении эпюры изгибающих моментов мы не воспользовались одной из опорных реакций — реакцией RD, так как вычисления 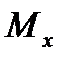 проводили с двух сторон от сечения D (слева на право и справа налево). Как видим, можно было в начальной стадии вместо трех уравнений равновесия
проводили с двух сторон от сечения D (слева на право и справа налево). Как видим, можно было в начальной стадии вместо трех уравнений равновесия 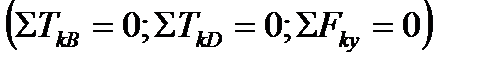 оставить лишь одно
оставить лишь одно 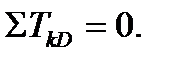
Из условия прочности балки при изгибе определяем размеры ее поперечного сечения. В опасном сечении (сечение С) взятый по абсолютному значению изгибающий момент 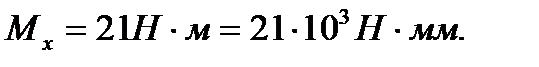
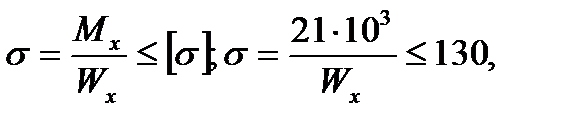
отсюда требуемый осевой момент сопротивления Wx = 162 мм3. Для квадрата момент сопротивления 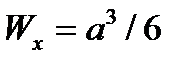 . Приравнивая
. Приравнивая 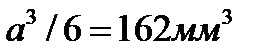 , находим сторону квадрата а = 9,9 мм. Принимаем а = 10 мм.
, находим сторону квадрата а = 9,9 мм. Принимаем а = 10 мм.
Дата добавления: 2015-02-05; просмотров: 3424;
