Поверхностное натяжение

Ближний порядок имеет место в жидкости вследствие того, что между ее молекулами действуют достаточно большие силы притяжения. Если молекула жидкости находится в глубине, то она окружена со всех сторон другими молекулами и действующая на нее результирующая сила притяжения равна нулю. 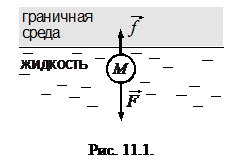Если же молекула находится вблизи поверхности соприкосновения жидкости с другой средой, например, с воздухом, с другой жидкостью или со стенками сосуда, то результирующая сила ее притяжения другими молекулами жидкости в общем случае отличается от результирующей силы взаимодействия этой молекулы с граничной средой. Поэтому на молекулу , находящуюся в поверхностном слое жидкости, действует равнодействующая сил притяжения, направленная либо внутрь жидкости, либо внутрь граничной среды, рис. 11.1. Например, если жидкость граничит с собственным насыщенным паром, то 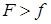и равнодействующая сила направлена внутрь жидкости, поскольку плотность молекул в жидкости велика по сравнению с плотностью молекул газовой среды (при температуре, не равной критической).

Рассмотрим случай 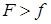. Для перемещения некоторой молекулы 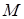жидкости из глубины к поверхности внешняя сила, действующая на жидкость и через нее на молекулу 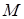, должна компенсировать силу, «втягивающую» молекулу вглубь, и совершить некоторую положительную работу. Отсюда следует, что увеличение площади поверхности жидкости, то есть увеличение числа молекул в поверхностном слое, сопровождается совершением положительной работы внешними силами, действующими на жидкость. Таким образом, жидкость ведет себя так, как будто ее поверхность покрыта пленкой, находящейся в состоянии напряжения («натянутой» пленкой). Поверхностным натяжением объясняется, в частности, сферическая форма свободно падающих капель жидкости или принятие формы шара жидкостью, выплеснутой из сосуда в условиях невесомости, например, на космическом корабле, вращающемся вокруг Земли.

Напротив, если 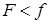, то жидкость ведет себя так, как будто она обтянута пленкой, находящейся в сжатом состоянии.

Количественной характеристикой величины напряжения поверхностного слоя жидкости является коэффициент поверхностного натяжения (КПН).

Коэффициентом поверхностного натяжения называется работа, которую следует совершить, чтобы изотермически и квазистатически увеличить площадь поверхности жидкости на единицу при неизменном объеме.

Квазистатичность (предельная медленность) изменения поверхности жидкости означает, что жидкость не должна получить какое-либо приращение кинетической энергии, так что вся затраченная работа идет на преодоление сил поверхностного натяжения.

Определение понятия КПН применимо к жидкости, граничащей с газом, другой жидкостью и твердым телом.

КПН зависит от того, с какой средой граничит жидкость. В таблицах физических величин приводятся обычно значения КПН жидкостей, граничащих со своим насыщенным паром или с воздухом.

Пример 11.2. Прямоугольная проволочная рамка затянута мыльной пленкой с коэффициентом поверхностного натяжения 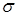. Сторона 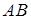является подвижной, ее длина равна 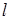, рис. 11.2. Какую силу 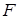необходимо приложить к стороне 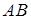для того, чтобы удерживать ее в неподвижном состоянии?

Переместим сторону 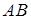на 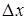. Приращение 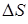площади поверхности мыльной пленки равно (с учетом того, что пленка имеет две стороны). Согласно определению КПН, работа силы 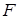, действующей на сторону 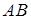, равна 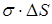. Эта же работа равна 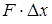. Находим, что

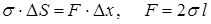. (11.1)

* * *

Эквивалентным приведенному выше определению КПН является следующее определение:коэффициент поверхностного натяжения равен силе, действующей на единицу длины разреза пленки на поверхности жидкости.

Применим последнееопределение к задаче, рассмотренной в примере 11.2. Общая «длина разреза» поверхности мыльной пленки вблизи стороны , учитывая двусторонность пленки, равна 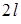. Сила, действующая на единицу длины разреза, равна 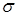, а на весь разрез, то есть на сторону 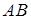, действует сила 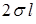, что совпадает с результатом (11.1), полученным с использованием первого определения КПН.

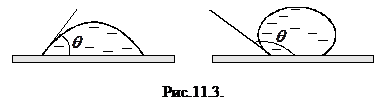В случае, когда жидкость граничит одновременно с твердым телом и с воздухом, в качестве величины, характеризующей взаимодействие между молекулами у границы раздела сред, удобно использовать краевой угол 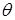, образуемый поверхностью капли жидкости с плоской твердой поверхностью, рис. 11.3. Если 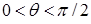, то говорят, что имеет место частичное смачивание жидкостью твердой поверхности. При 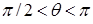говорят о частичном несмачивании. Пр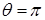и и 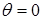говорят соответственно ополном несмачивании и полном смачивании. Полное несмачивание имеет место, например, при нахождении капли ртути на поверхности стекла. Полное смачивание имеет место при попадании капли бензина на поверхность воды - капля расте­кается по поверхности в моно­молекулярный слой, то есть слой с толщиной, близкой к размеру молекул.

Понятие краевого угла вообще-то применимо и для границ «жидкость – жидкость - газ», «жидкость – жидкость - жидкость», «твердое тело - жидкость - жидкость», причем краевой угол оказывается возможным выразить через комбинацию соответствующих коэффициентов поверхностного натяжения различных пар сред.

Краевой угол характеризует взаимодействие молекул на границе трех сред, тогда как КПН характеризует взаимодействие молекул двух соприкасающихся сред.

11.3. Разность давлений по разные стороны искривленной поверхности
жидкости

Рассмотрим плоскую натянутую пленку, например, от надувного резинового шарика. Чтобы сделать ее поверхность изогнутой, необходимо создать разность давлений по разные стороны пленки, например, надавить на одну из сторон пальцем.

Неподвижная поверхность жидкости, граничащей с газом, подобна натянутой пленке. Если эта поверхность искривлена (как, например, поверхность капли или поверхность жидкости у стенки сосуда), то это означает, что имеется разность давлений по разные ее стороны. Давление меньше с той стороны, с которой поверхность жидкости выглядит выпуклой, рис. 11.4.

Вычислим разность давлений по разные стороны находящейся в статическом состоянии цилиндрической поверхности жидкости с КПН, равным , радиус кривизны поверхности . Выделим на поверхности прямоугольный элемент 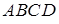, стороны 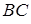и 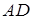которого являются дугами, стягиваемыми предельно малым углом 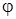, рис. 11.5 а. На каждую из сторон 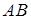и 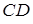, длины которых равны 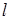, действует сила поверхностного натяжения 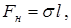направленная касательно к поверхности и нормально к соответствующей стороне. Проекция 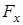каждой из этих сил на направление оси 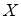, нормальной к поверхности выделенного элемента 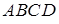, рис. 11.5 б, равна:

.

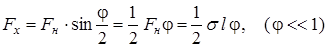Результирующая сила 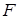, действующая на элемент 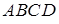, направлена вдоль оси 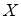и равна ,

.

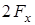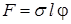Давление 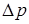, которое создает сила 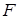, воздействуя на элемент 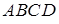, равно:

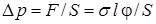, (11.2)

где 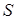- площадь элемента, равная 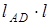, 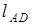- длина дуги 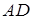. Учитывая, что 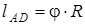, находим:

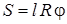. (11.3)

Из (11.2), (11.3) получим:

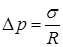. (11.4)

Обозначим через 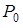и 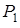давления в жидкости по разные стороны поверхности элемента . Учитывая, что выделенный элемент, по условию, неподвижен, заключаем, что 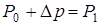, или

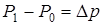. (11.5)

Таким образом, формула (11.4) определяет разность давлений по разные стороны цилиндрически искривленной поверхности жидкости, обусловленную поверхностным натяжением.

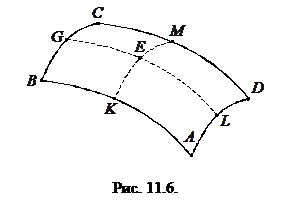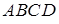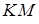В общем случае поверхность жидкости является двояко искривленной. Рассмотрим малый прямоугольный элемент такой поверхности, рис. 11.6. Выберем на элементе точку и проведем через нее две дуги и 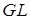, нормальные сторонам элемента. Радиусы кривизны дуг обозначим через 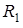и 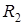. Повторяя выкладки, аналогичные проде­ланным выше для элемента цилиндрической поверхности, и учитывая при этом силы натяжения, действующие как на стороны 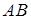и 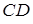, так и на стороны 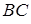и 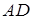элемента 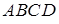, получим для давления, действующего на элемент вследствие поверхностного натяжения:

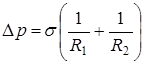. (11.6)

Формула (11.6), впервые полученная Лапласом, определяет разность давлений по разные стороны искривленной поверхности жидкости. Если поверхность является цилиндрической, то один из радиусов кривизны в (11.6) следует положить бесконечно большим и (11.6) переходит в (11.4). Если поверхность сферическая, то в (11.6) следует положить .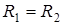

Отметим, что в дифференциальной геометрии доказывается следующее утверждение: если через некоторую точку на искривленной поверхности провести две взаимно перпендикулярные дуги с радиусами кривизны 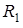и 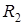, то величина не зависит от того, как выбраны эти дуги.

Итак, кривизна поверхности жидкости означает, что имеет место разность давлений по разные стороны поверхности, определяемая формулами (11.5), (11.6) и называемая капиллярным давлением. Давление больше с той стороны поверхности, с которой она выглядит вогнутой.

Пример 11.3. Капля ртути имеет диаметр . Коэффициент поверхностного натяжения ртути 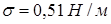. Вычислим давление внутри капли при атмосферном давлении .

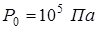Воспользуемся формулами (11.5), (11.6), положив 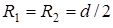, получим для давления 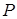внутри капли:

.

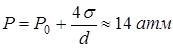Задача 11.1. Вычислить капиллярное давление воздуха внутри мыльного пузырька радиуса 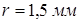. КПН мыльной пленки равен .

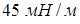Ответ: .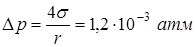

Указание. Учесть, что у мыльной пленки есть внешняя и внутренняя поверхность, натяжение каждой из которых вносит вклад в капиллярное давление.

Задача 11.2. В сосуде с воздухом при давлении 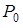находится мыльный пузырек диаметра 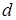. Давление воздуха в сосуде изотермически уменьшили в 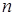раз, в результате чего диаметр пузырька увеличился в 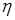раз. Найти поверхностное натяжение мыльной воды.

Ответ: .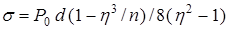

Указание. Учесть, что воздух в пузырьке совершает изотермическое расширение.