Глава 30. Элементы квантовой статистики

28.1. Свободная частица движется со скоростью и. Доказать, что выполняется соотношение .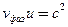

28.2. Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 1% от ее числового значения, определить неопределенность координаты электрона. Применительно ли в данном случае для электрона понятие траектории? [ 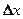= 33 нм; нет]

28.3. 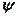-Функция некоторой частицы имеет вид 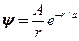, где r — расстояние этой частицы от силового центра, а — постоянная. Определить среднее расстояние 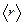частицы от силового центра. [ 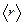= а/2]

28.4. Записать уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода.

28.5. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Определить вероятность W обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 2). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. [W = 0,195]

28.6. Прямоугольный потенциальный барьер имеет ширину 0,1 нм. Определить в электрон-вольтах разность энергий U – E, при которой вероятность прохождения электрона сквозь барьер составит 0,99. [0,1 мэВ]

Глава 30. Элементы квантовой статистики