ДИФРАКЦІЯ НА ЩІЛИНІ
1. Теоретична частина
Дифракцією світла називається огинання світловими хвилями перешкод (порівнянних з довжиною хвилі) з наступною інтерференцією цих хвиль. При дифракції світло може проникати в область геометричної тіні й, навпаки, в областях, які з міркувань геометричної оптики повинні бути освітлені, світло може бути відсутнім. Явище дифракції можна пояснити й описати за допомогою принципів Гюйгенса і Гюйгенса-Френеля.
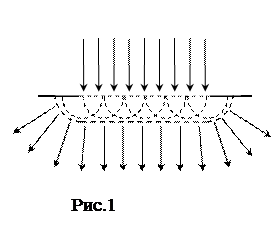 Принцип Гюйгенса говорить: кожна точка хвильового фронту є джерелом вторинних сферичних хвиль, огинаюча яких дає новий хвильовий фронт. Таким чином, принцип Гюйгенса дозволяє знаходити розміщення фронту хвилі в наступний момент часу, якщо відомо його розміщення в попередній момент часу. За допомогою принципу Гюйгенса можна знайти, наприклад, положення хвильового фронту після проходження світлом щілини (рис.1). Видно, що хвильовий фронт, побудований, як огинаюча вторинних сферичних хвиль, поблизу країв щілини викривляється, і світло заходить в область геометричної тіні - спостерігається дифракція світла. Однак принцип Гюйгенса не говорить про те, чому дорівнює інтенсивність світла, що поширюється в різних напрямках.
Принцип Гюйгенса говорить: кожна точка хвильового фронту є джерелом вторинних сферичних хвиль, огинаюча яких дає новий хвильовий фронт. Таким чином, принцип Гюйгенса дозволяє знаходити розміщення фронту хвилі в наступний момент часу, якщо відомо його розміщення в попередній момент часу. За допомогою принципу Гюйгенса можна знайти, наприклад, положення хвильового фронту після проходження світлом щілини (рис.1). Видно, що хвильовий фронт, побудований, як огинаюча вторинних сферичних хвиль, поблизу країв щілини викривляється, і світло заходить в область геометричної тіні - спостерігається дифракція світла. Однак принцип Гюйгенса не говорить про те, чому дорівнює інтенсивність світла, що поширюється в різних напрямках.
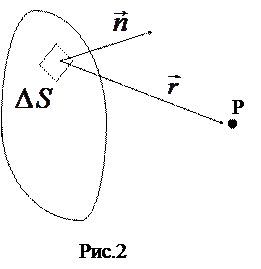
 Кількісне описання дифракції можливо на основі принципу Гюйгенса, доповненого Френелем припущенням про когерентність вторинних хвиль і їх інтерференції. Принцип Гюйгенса-Френеля складається з двох частин:
Кількісне описання дифракції можливо на основі принципу Гюйгенса, доповненого Френелем припущенням про когерентність вторинних хвиль і їх інтерференції. Принцип Гюйгенса-Френеля складається з двох частин:
|
2. Всі точки фронту хвилі виконують коливання з однаковою частотою і однаковою фазою і, отже, уявляють собою сукупність когерентних джерел. Інтенсивність світла в будь-якій точці простору перед хвильовим фронтом визначається результатом інтерференції вторинних хвиль, що доходять до цієї точки. Таким чином, щоб розрахувати інтенсивність світла в якій-небудь точці Р (рис.2) перед хвильовим фронтом, необхідно скласти коливання, що приходять у цю точку від усіх ділянок хвильового фронту. При цьому потрібно враховувати їх амплітуди і фази. Амплітуда коливань, що приходять у точку Р від ділянки поверхні хвильового фронту  , залежить від розмірів цієї ділянки, від відстані r від нього до точки Р та від кута між вектором
, залежить від розмірів цієї ділянки, від відстані r від нього до точки Р та від кута між вектором 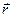 і нормаллю до поверхні
і нормаллю до поверхні 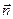 ; фаза коливань визначається довжиною шляху r, пройденого вторинними хвилями. Додавання таких елементарних коливань є завданням інтегрального обчислення й може бути досить складним. Але в найпростіших випадках інтегрування може бути замінене простим додаванням.
; фаза коливань визначається довжиною шляху r, пройденого вторинними хвилями. Додавання таких елементарних коливань є завданням інтегрального обчислення й може бути досить складним. Але в найпростіших випадках інтегрування може бути замінене простим додаванням.
 Дифракція Фраунгофера на щілині. Дифракція Фраунгофера спостерігається в паралельних променях, тобто, коли хвильовий фронт падаючої хвилі – плоский. Плоский хвильовий фронт має лазерне випромінювання, крім того, випромінювання лазера когерентно й монохроматично. Схема спостереження дифракції Фраунгофера від однієї щілини показана на рис.3. Паралельний пучок світла від напівпровідникового лазера 1 падає нормально на щілину 2, довжина якої набагато більша її ширини b. Світло дифрагує на щілині, тобто розділяється на пучки, що йдуть під різними кутами від первісного напрямку. Дифракційну картину можна спостерігати на екрані 3. Відстань від щілини до екрана дорівнює
Дифракція Фраунгофера на щілині. Дифракція Фраунгофера спостерігається в паралельних променях, тобто, коли хвильовий фронт падаючої хвилі – плоский. Плоский хвильовий фронт має лазерне випромінювання, крім того, випромінювання лазера когерентно й монохроматично. Схема спостереження дифракції Фраунгофера від однієї щілини показана на рис.3. Паралельний пучок світла від напівпровідникового лазера 1 падає нормально на щілину 2, довжина якої набагато більша її ширини b. Світло дифрагує на щілині, тобто розділяється на пучки, що йдуть під різними кутами від первісного напрямку. Дифракційну картину можна спостерігати на екрані 3. Відстань від щілини до екрана дорівнює 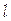 .
.
Задача дифракції полягає в знаходженні розподілу інтенсивності в дифракційній картині (на екрані). Знайдемо, яку інтенсивність мають дифраговані промені, що йдуть під деяким кутом  від попереднього напрямку в деяку точку Р на екрані (рис.4а). Для цього скористаємося принципом Гюйгенса-Френеля: кожна точка хвильового фронту (на щілині) є джерелом вторинних когерентних хвиль; інтенсивність світла у точці Р є результатом інтерференції цих вторинних хвиль. Розіб'ємо хвильовий фронт у площині щілини на елементарні зони шириною
від попереднього напрямку в деяку точку Р на екрані (рис.4а). Для цього скористаємося принципом Гюйгенса-Френеля: кожна точка хвильового фронту (на щілині) є джерелом вторинних когерентних хвиль; інтенсивність світла у точці Р є результатом інтерференції цих вторинних хвиль. Розіб'ємо хвильовий фронт у площині щілини на елементарні зони шириною 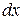 , паралельні краям щілини (рис.4в). Вторинні хвилі, що посилаються цими зонами під кутом
, паралельні краям щілини (рис.4в). Вторинні хвилі, що посилаються цими зонами під кутом  , потраплять у точку Р. Для даної геометрії експерименту ( тобто у випадку плоского фронту падаючої хвилі й відстані до екрана багато більшої ширини щілини) вторинні хвилі, що йдуть під усіма кутами можна вважати плоскими. Тоді кожна елементарна зона дасть свій внесок
, потраплять у точку Р. Для даної геометрії експерименту ( тобто у випадку плоского фронту падаючої хвилі й відстані до екрана багато більшої ширини щілини) вторинні хвилі, що йдуть під усіма кутами можна вважати плоскими. Тоді кожна елементарна зона дасть свій внесок 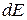 у коливання в точці Р у такому виді:
у коливання в точці Р у такому виді:
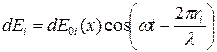 (1)
(1)
- це рівняння плоскої хвилі, у ньому:
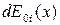 - амплітуда коливань в елементарній зоні (залежить від площі зони),
- амплітуда коливань в елементарній зоні (залежить від площі зони),
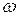 - циклічна частота,
- циклічна частота,
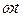 - фаза коливань на поверхні кожної із зон (якщо коливання в площині щілини описуються рівнянням
- фаза коливань на поверхні кожної із зон (якщо коливання в площині щілини описуються рівнянням 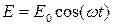 ),
),
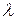 - довжина хвилі,
- довжина хвилі,
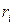 - відстань від
- відстань від 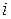 -ої зони до точки Р (залежить від х і кута
-ої зони до точки Р (залежить від х і кута  ),
),
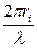 - внесок у фазу, пов'язаний із проходженням хвилею відстані
- внесок у фазу, пов'язаний із проходженням хвилею відстані 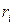 .
.
 |
Коливання
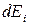 будуть складатися, тобто буде відбуватися інтерференція, внаслідок чого результуюче коливання в точці Р буде рівним
будуть складатися, тобто буде відбуватися інтерференція, внаслідок чого результуюче коливання в точці Р буде рівним
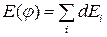 або
або  . (2)
. (2)
Для знаходження 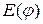 нам потрібно розрахувати
нам потрібно розрахувати 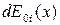 й
й 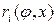 .
.
Для невеликих кутів дифракції амплітуда коливання 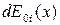 , що посилається зоною в будь-яку точку екрана, буде залежати тільки від площі зони (і не залежати від кута дифракції). Площа пропорційна ширині зони
, що посилається зоною в будь-яку точку екрана, буде залежати тільки від площі зони (і не залежати від кута дифракції). Площа пропорційна ширині зони 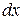 , сумарна амплітуда всіх зон рівна
, сумарна амплітуда всіх зон рівна 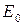 , ширина щілини рівна
, ширина щілини рівна 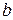 . Отже, амплітуда коливання
. Отже, амплітуда коливання 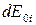 , що спричинена зоною шириною
, що спричинена зоною шириною 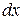 в будь-якій точці екрана, може бути представлена у вигляді:
в будь-якій точці екрана, може бути представлена у вигляді:
 (3)
(3)
Тепер визначимо відстані 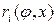 , що проходять вторинні хвилі з різних зон у точку Р. Нехай відстань, пройдена вторинною хвилею від зони, пов'язаною з лівим краєм щілини, дорівнює
, що проходять вторинні хвилі з різних зон у точку Р. Нехай відстань, пройдена вторинною хвилею від зони, пов'язаною з лівим краєм щілини, дорівнює 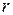 (рис.4а). Тоді шлях, пройдений інший хвилею від зони, що міститься від краю на відстані
(рис.4а). Тоді шлях, пройдений інший хвилею від зони, що міститься від краю на відстані 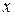 , буде
, буде 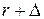 . На рис.4б у збільшеному масштабі показана ілюстрація для знаходження
. На рис.4б у збільшеному масштабі показана ілюстрація для знаходження 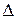 . Із простих геометричних міркувань видно, що
. Із простих геометричних міркувань видно, що
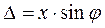 . (4)
. (4)
Підставимо отримані результати для 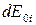 і
і 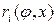 у формулу (1):
у формулу (1):
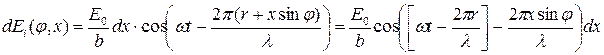 (5)
(5)
Таким чином, коливання, створюване елементарною зоною з координатою х уточці Р(положення якої на екрані визначається кутом  ), визначається формулою (5). Результуюче коливання, створюване в точці Русією відкритою ділянкою хвильової поверхні, знайдемо, зінтегрувавши
), визначається формулою (5). Результуюче коливання, створюване в точці Русією відкритою ділянкою хвильової поверхні, знайдемо, зінтегрувавши 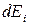 за шириною щілини
за шириною щілини 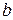 :
:
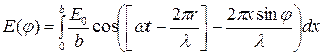 . (6)
. (6)
Позначивши незалежні від 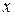 величини в підінтегральному виразі як
величини в підінтегральному виразі як  і
і 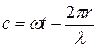 , одержимо інтеграл виду
, одержимо інтеграл виду
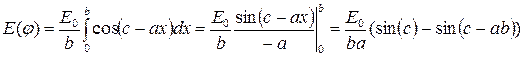 (7)
(7)
Скориставшись тригонометричною тотожністю 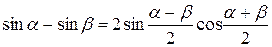 , дістанемо
, дістанемо
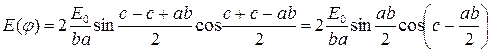 .
.
Підставивши сюди значення 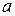 і
і 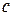 , знайдемо
, знайдемо
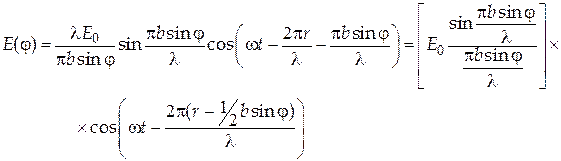
Вираз, що знаходиться під знаком косинуса, залежить від часу й показує фазу коливань; модуль виразу, що знаходиться у квадратних дужках, дає амплітуду 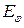 результуючого коливання в точці Р(положення якої визначається кутом
результуючого коливання в точці Р(положення якої визначається кутом  ):
):
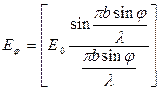 (8)
(8)
Для точки, що лежить проти центру щілини 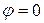 . Підстановка цього значення у формулу (8) дає
. Підстановка цього значення у формулу (8) дає 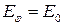 (
( 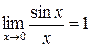 ). Цей результат можна одержати більш простим шляхом. При
). Цей результат можна одержати більш простим шляхом. При 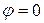 коливання від усіх елементарних зон приходять у точку Ру однаковій фазі. Тому амплітуда результуючого коливання дорівнює алгебраїчній сумі амплітуд коливань, що додаються.
коливання від усіх елементарних зон приходять у точку Ру однаковій фазі. Тому амплітуда результуючого коливання дорівнює алгебраїчній сумі амплітуд коливань, що додаються.
При значеннях  , що задовольняють умові:
, що задовольняють умові: 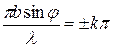 , тобто у випадку, коли
, тобто у випадку, коли
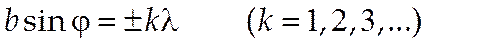
| (9) |
амплітуда 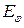 стає рівною нулю.. Таким чином, умова (9) визначає положення мінімумів інтенсивності в дифракційній картині.
стає рівною нулю.. Таким чином, умова (9) визначає положення мінімумів інтенсивності в дифракційній картині.
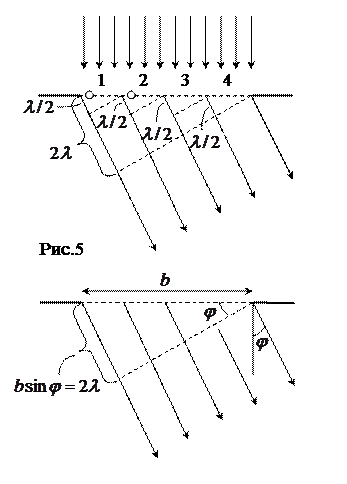 Умову(9) легко одержати з наступних міркувань. Якщо різниця ходу
Умову(9) легко одержати з наступних міркувань. Якщо різниця ходу 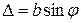 від країв щілини рівна
від країв щілини рівна 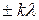 , відкриту частину хвильової поверхні можна розбити на парне число
, відкриту частину хвильової поверхні можна розбити на парне число 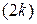 рівних по ширині зон, таких, що різниця ходу від країв кожної зони буде рівна
рівних по ширині зон, таких, що різниця ходу від країв кожної зони буде рівна 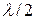 (див. рис.5, виконаний для
(див. рис.5, виконаний для 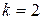 - чотирьох зон). Коливання, що посилаютьcя у точку спостереження Р відповідними ділянками двох сусідніх зон (наприклад, позначеними кружками ділянками зон 1 і 2), перебувають у протифазі (різниця ходу між ними рівна
- чотирьох зон). Коливання, що посилаютьcя у точку спостереження Р відповідними ділянками двох сусідніх зон (наприклад, позначеними кружками ділянками зон 1 і 2), перебувають у протифазі (різниця ходу між ними рівна 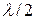 ). Тому коливання від кожної пари сусідніх зон взаємно гасять один одного й результуюча амплітуда в точці Р дорівнює нулю.
). Тому коливання від кожної пари сусідніх зон взаємно гасять один одного й результуюча амплітуда в точці Р дорівнює нулю.
При різниці ходу від країв щілини, 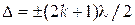 , тобто при непарнім числі зон, дія однієї з них виявиться не компенсованою. Таким чином, умова максимуму при дифракції на щілині буде:
, тобто при непарнім числі зон, дія однієї з них виявиться не компенсованою. Таким чином, умова максимуму при дифракції на щілині буде:
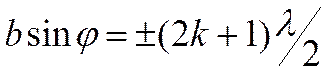
| (10) |
Інтенсивність світла пропорційна квадрату амплітуди. Отже, з формули (8) випливає вираз для кутового розподілу інтенсивності світла при дифракції на щілині:
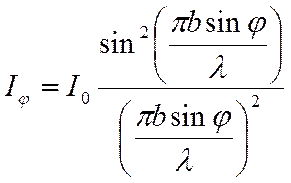
| (11) |
де 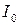 - інтенсивність світла в середині дифракційної картини;
- інтенсивність світла в середині дифракційної картини; 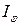 - інтенсивність у точці, положення якої визначається даним значенням кута
- інтенсивність у точці, положення якої визначається даним значенням кута  .
.
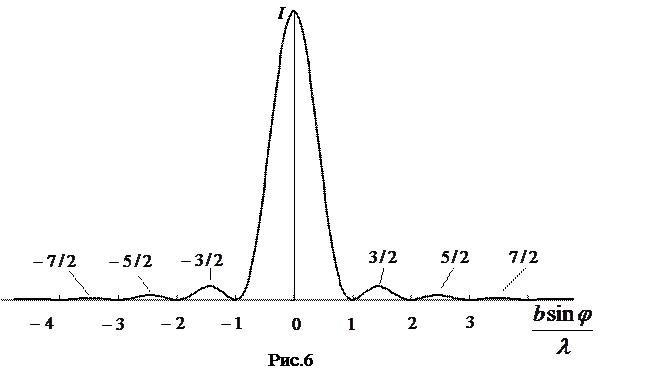 З формули (11) випливає, що
З формули (11) випливає, що 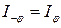 . Це означає, що дифракційна картина симетрична. Графік функції (11) зображений на рис.6. По осі абсцис відкладені значення
. Це означає, що дифракційна картина симетрична. Графік функції (11) зображений на рис.6. По осі абсцис відкладені значення 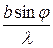 , по осі ординат - інтенсивність
, по осі ординат - інтенсивність 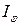 . Якщо
. Якщо 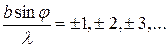 то вирази під знаком синуса у формулі (11) дорівнюють
то вирази під знаком синуса у формулі (11) дорівнюють  синус стає рівним нулю і спостерігаються мінімуми дифракції. Видно, що вищезгадана умова збігається з умовою (9). При
синус стає рівним нулю і спостерігаються мінімуми дифракції. Видно, що вищезгадана умова збігається з умовою (9). При  (умова (10)) синус у виразі (11) стає рівним
(умова (10)) синус у виразі (11) стає рівним  , і спостерігаються дифракційні максимуми. Якщо прийняти інтенсивність нульового (центрального) максимуму за одиницю (
, і спостерігаються дифракційні максимуми. Якщо прийняти інтенсивність нульового (центрального) максимуму за одиницю ( 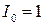 ) то з (11) інтенсивність першого максимуму буде
) то з (11) інтенсивність першого максимуму буде 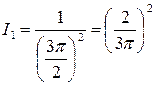 , другого -
, другого - 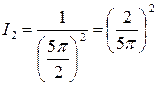 ,
, 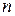 -го -
-го - 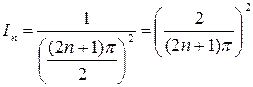 . Таким чином, мають місце наступні співвідношення інтенсивностей у максимумах:
. Таким чином, мають місце наступні співвідношення інтенсивностей у максимумах:
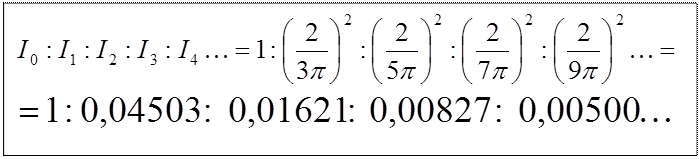 Таким чином, центральний максимум значно (~ в 20 раз) перевершує по інтенсивності інші максимуми; у ньому зосереджується основна частка світлового потоку, що пройшов через щілину. Інтенсивності в наступних максимумах порівняні. Якщо за 1 прийняти інтенсивність 1-го максимуму, то їх співвідношення буде таким
Таким чином, центральний максимум значно (~ в 20 раз) перевершує по інтенсивності інші максимуми; у ньому зосереджується основна частка світлового потоку, що пройшов через щілину. Інтенсивності в наступних максимумах порівняні. Якщо за 1 прийняти інтенсивність 1-го максимуму, то їх співвідношення буде таким
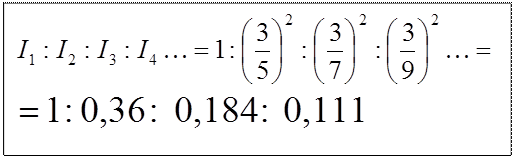
 |
Кількість мінімумів інтенсивності визначається відношенням ширини щілини 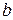 й довжини хвилі
й довжини хвилі 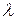 . З умови мінімуму (9)
. З умови мінімуму (9) 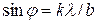 . Модуль
. Модуль 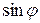 не може перевершити одиницю. Тому
не може перевершити одиницю. Тому 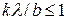 , звідки найбільше число спостережуваних дифракційних максимумів або мінімумів повинне бути
, звідки найбільше число спостережуваних дифракційних максимумів або мінімумів повинне бути
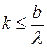 (13)
(13)
При ширині щілини, меншої довжини хвилі, мінімуми взагалі не виникають. У цьому випадку інтенсивність світла монотонно спадає від середини картини до її країв.
2. Експериментальна частина.
Метою даної роботи є:
1. Визначення ширини щілини за допомогою дифракційних вимірів;
2. Перевірка співвідношення 12) інтенсивностей максимумів при дифракції на щілині.
Схема експериментальної установки представлена на рис.7 (вид зверху). Джерелом світла служить напівпровідниковий лазер ПЛ, який дає вузький пучок монохроматичного випромінювання. Випромінювання лазера попадає на вертикальну щілину Щ і дифрагує. Дифракційна картина проектується на лінійку Л2, по якій може переміщатися фотодіод ФД. Напруга на фотодіоді, пропорційна інтенсивності світла, виміряється мілівольтметром мВ. Відстань від щілини до фотодіода може мінятися й вимірюється лінійкою Л1.
 Порядок проведення вимірів.
Порядок проведення вимірів.
1. Вимірюють і записують відстань від щілини до фотодіода 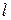 .
.
2. Вимірюють темнову напругу на фотодіоді 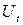 (тобто, коли лазер виключений).
(тобто, коли лазер виключений).
3. Включають лазер і спостерігають дифракційну картину.
4. За допомогою лінійки Л2 вимірюють положення вперших чотирьох дифракційних максимумів і мінімумів і заносять у таблицю 1. Виміри повторюють три рази й знаходять середні значення уср.
5. Переміщають фотодіод на перший правий дифракційний максимум і записують напругу 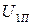 , пропорційну інтенсивності в ньому в таблицю 1. Переміщуючи фотодіод, записують напруги U, що відповідають наступним трьом максимумам праворуч від центрального. Виміри повторюють три рази й знаходять середні значення Uср. Ті ж самі дії проробляють для лівої частини дифракційної картини.
, пропорційну інтенсивності в ньому в таблицю 1. Переміщуючи фотодіод, записують напруги U, що відповідають наступним трьом максимумам праворуч від центрального. Виміри повторюють три рази й знаходять середні значення Uср. Ті ж самі дії проробляють для лівої частини дифракційної картини.
6. Розраховують ширину щілини: для дифракційних мінімумів з формули (9) 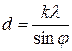 ; при малих кутах дифракції
; при малих кутах дифракції 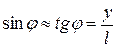 й тоді
й тоді
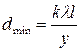 , (13)
, (13)
(усі величини y, l, l підставляють у мм і d одержують у мм), результати заносять у таблицю. Аналогічно для максимумів: з (10) 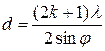 і
і
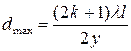 . (14)
. (14)
Потім усереднюють розраховані за формулами (13) і (14) величини 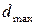 і
і  :
: 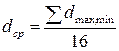 =...
=...
7. Для перевірки співвідношення (12), знаходять відносні інтенсивності максимумів перших чотирьох порядків з врахуванням темнової напруги:  . Результати заносять у таблицю.
. Результати заносять у таблицю.
8. Будують графік залежності відносної інтенсивності 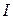 від величини
від величини 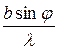 , на цьому ж графіку будують теоретичну залежність Iтеор (графіки аналогічні представленому на рис.6). Порівнюють отримані криві.
, на цьому ж графіку будують теоретичну залежність Iтеор (графіки аналогічні представленому на рис.6). Порівнюють отримані криві.
Таблиця 1.
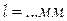 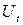 =…мВ =…мВ 
| ||||||||||||||
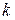
| b, мм | 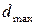  мм мм
| 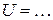 мВ мВ
| I | Iтеор | 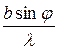
| ||||||||
| уср | Uср | |||||||||||||
| праворуч | max | 0,111 | 3,5 | |||||||||||
| min | ||||||||||||||
| max | 0,184 | 3,5 | ||||||||||||
| min | ||||||||||||||
| max | 0,36 | 2,5 | ||||||||||||
| min | ||||||||||||||
| Max | 1,5 | |||||||||||||
| min | ||||||||||||||
| праворуч | min | |||||||||||||
| max | 1,5 | |||||||||||||
| min | ||||||||||||||
| max | 0,36 | 2,5 | ||||||||||||
| min | ||||||||||||||
| max | 0,184 | 3,5 | ||||||||||||
| min | ||||||||||||||
| max | 0,111 | 3,5 |
Контрольні питання.
1. Що таке дифракція світла?
2. Сформулюйте принцип Гюйгенса-Френеля.
3. При яких умовах спостерігаються максимуми й мінімуми дифракції на щілині?
4. Виведіть співвідношення (9), (10) і (11).
5. Чим визначається максимальне число дифракційних максимумів?
ЛІТЕРАТУРА.
1. Общая фізика / В.І.Михайленко, В.М.Белоус, Ю.М.Поповский. -К.: ИСДО, 1993.
2. Курс общей физики. Том III/ І.В.Савельев. - М.: Наука, 1967.
3. Курс общей физики. Тому III/ С.Є.Фриш і А.В.Тиморева. - М.: ГИФМЛ, 1962. 
Дата добавления: 2015-01-15; просмотров: 10624;
