Втискування сферичного індентора

Деформування порід при втискуванні жорсткого сферичного індентора і плоского циліндричного штампа багато в чому схожі, хоча є і суттєві відмінності.

При відсутності навантаження сфера контактує з поверхнею твердого тіла в точці. Із збільшенням навантаження на сферу формується кругова площадка контакту. Розв’язок про радіус контактної поверхні, розподіл тиску на площадці і про вертикальні переміщення точок поверхні отримано Герцем. Розрахункова схема і розподіл контактних тисків показано на рис. 10.7.

Радіус площадки контакту дорівнює

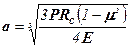, (10.10)

де R_С – радіус сфери.

Найбільший тиск має місце в центрі поверхні кон­такту і складає

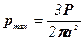, (10.11)

а розподіл тиску по діамет­ральному січенню площадки кон­такту описується рівнянням еліпса

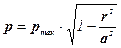. (10.12)

Найбільше переміщення цен­тральної точки контакту дорівнює

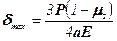. (10.13)

Згідно досліджень Ейгелеса Р.М. структура поля напружень така ж, як і під циліндричним штампом. Відмінність полягає в тому, що уже на поверхні контакту має місце нерівномірний усесторонній стиск, а область усестороннього стиску при втискуванні сфери значно менша, чим при втискуванні плоского штампу. Розподіл напружень на осі симетрії під сферичним штампом показана на рис 24. Дотичні напруження досягають найбільших значень на деякій глибині від поверхні контакту (близько 0,5 а).

Таким чином, при втискуванні сфери найімовірнішими місцями руйнування є: на поверхні – центр контактної площадки, а в масиві – зона на глибині, що дорівнює половині радіуса контактної площадки.