Моделирование ситуаций

Моделирование является основным методом исследования производственно-экономических систем. Под моделированием понимается такой способ отображения объективной реальности, при котором для изучения оригинала применяется специально построенная модель, воспроизводящая определенные (как правило, лишь существенные) свойства исследуемого реального явления (процесса).

Модель – это объект любой природы, который способен замещать исследуемый объект так, что его изучение дает новую информацию об исследуемом объекте.

В соответствии с этими определениями в понятие моделирования входит построение модели (квазиобъекта) и операции над ней для получения новой информации об исследуемом объекте. С позиций использования под моделью можно понимать удобное для анализа и синтеза отображение системы. Между системой и ее моделью существует отношение соответствия, которое и позволяет исследовать систему посредством исследования модели.

Тип модели определяется в первую очередь вопросами, на которые желательно получить ответ при помощи модели. Возможна различная степень соответствия модели и моделируемой системы.

Часто модель отображает только функцию системы, а структура модели (и ее адекватность системе) не играет роли, она рассматривается как черный ящик.

Имитационная модель включает уже единое отображение и функции системы, и существа происходящих в ней процессов.

Моделирование как метод познания основано на том, что все модели так или иначе отображают действительность. В зависимости оттого, как и какими средствами, при каких условиях, по отношению к каким объектам познания реализуется это их свойство, возникает большое разнообразие моделей. Существует ряд принципов классификации моделей разной природы, из которых наиболее существенными представляются следующие:

– по способу отображения действительности, а следовательно, и по аппарату построения (форма);

– по характеру моделируемых объектов содержание).

По способу отображения или аппарату построения различают два вида моделей (рис. 7.2): материальные и мысленные, или идеальные.

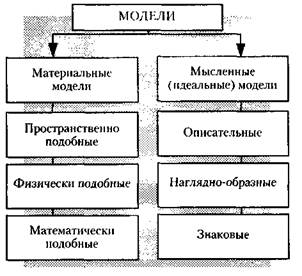
Рис. 7.2.Классификация моделей

Материальные модели – это модели, которые построены или отобраны человеком, существуют объективно, будучи воплощены в металле, дереве, стекле, электрических элементах биологических организациях и других материальных структурах.

Материальные моделиделятся на три подвида.

Пространственно подобные модели – сооружения, предназначенные для отображения пространственных свойств или отношений объекта (макеты домов, заводов, районов города, транспортной сети, расположения оборудования в цехе и т. д.). Обязательным условием таких моделей является геометрическое подобие.

Физически подобные модели – материальные модели, имеющие целью воспроизвести разного рода физические связи и зависимости изучаемого объекта (модели плотин электростанций кораблей и самолетов). Основой построения таких моделей является физическое подобие – одинаковость физической природы и тождественность законов движения.

Математически подобные модели - модели обладающие в той или иной степени одинаковым математическим формализмом, описывающим поведение объекта и модели (аналог ЭВМ, кибернетические функциональные модели). Математически подобные материальные модели – это вещественные или физические оболочки некоторых математических отношений, но не сами отношения.

Мысленные (или идеальные) моделиделятся на три подвида:

– описательные (концептуальные) модели, в которых отношения выражены в образах языка;

– наглядно-образные модели, образы которых в сознании построены из чувственно-наглядных элементов;

– знаковые (в том числе математические модели, в которых элементы объекта и их соотношения выражены при помощи знаков (в том числе математических символов и формул).

Классификацию моделей по характеру моделируемых объектов вследствие их чрезвычайного разнообразия приводить здесь не представляется целесообразным.

Конечной целью моделирования является изучение не модели как таковой, а некоторого отличного от нее, но воспроизводимого ею подлинного объекта изучения.

Очевидно, никакие модели не могут и не должны полностью воспроизводить все стороны и детали изучаемых явлений: предприятие может быть охарактеризовано с различных точек зрения – директора или главного инженера, бухгалтера, снабженца или энергетика. В соответствии с этим и характер, и построение модели будут различны.

Моделирование, как способ научного познания, основано на способности человека абстрагировать исходные признаки или свойства различных явлений (процессов) и устанавливать определенное соотношение между ними. Благодаря этому создается возможность исследовать явления или процессы косвенным путем, а именно изучением моделей, аналогичных им в некотором строго определенном отношении.

В общем случае целесообразна следующая последовательность моделирования систем: концептуальное описание (исследование) системы, ее формализация и, наконец, если это необходимо, алгоритмизация и квантификация системы.

При моделировании производственно-экономических систем наряду с формализованными, математическими методами анализа, используемыми для отдельных подсистем или частных процессов, приходится использовать также и эвристические методы анализа производства в тех его элементах и связях, которые не поддаются формализации. А при использовании математических методов вследствие множества переменных приходится зачастую прибегать к упрощениям, использовать методы декомпозиции и агрегирования переменных. В результате решения приобретают приближенный, качественный характер.

Вследствие наличия в больших сложных системах организационно-производственного управления звеньев и связей, которые трудно или вообще не формализуются, для их исследования приходится использовать в основном описательные модели, подвергая систему декомпозиции на отдельные функциональные подсистемы; затем искать те подсистемы, которые поддаются математической формализации, моделируя, таким образом, отдельные элементы общего производственного процесса.

Конечной целью моделирования производственно-экономической системы является подготовка и принятие руководителем предприятия управленческого решения.

Модели производственно-экономических системможно различать по следующим признакам:

– по целям моделирования;

– по задачам (функциям) управления;

– по этапам (процедурам) управления;

– по математическим методам моделирования.

В зависимости от целей моделирования различают модели, предназначенные для:

– проектирования систем управления;

– оценки эффективности;

– анализа возможностей предприятия в различных условиях его деятельности;

– выработки оптимальных решений в различных производственных ситуациях;

– расчета организационных структур системы управления;

– расчета информационного обеспечения и т. д.

Специфика моделей этого классификационного подразделения выражается в первую очередь в выборе соответствующих критериев эффективности, а также в процедуре реализации результатов моделирования.

В зависимости от задач (функций) управления различают модели календарного планирования, управления развитием предприятия, контроля качества продукции и т. д. Модели этого подразделения ориентированы на конкретные производственно-экономические задачи и, как правило, должны обеспечивать получение результатов в численном виде.

В зависимости от этапа (процедуры) автоматизации управления модели могут быть информационными, математическими, программными. Модели этого подразделения нацелены на соответствующие этапы движения и переработки информации.

В зависимости от применяемого математического аппарата модели можно разбить на пять больших групп: экстремальные, математического программирования (планирования), вероятностные, статистические и теоретико-игровые.

К экстремальным моделям относятся модели, дающие возможность отыскания экстремума функции или функционала. Сюда относятся модели, построенные с помощью графических методов, метода Ньютона и его модификаций, методов вариационного исчисления, принципа максимума Понтрягина и др. Исходя из возможностей этих методов они применяются в первую очередь для решения задач оперативного регулирования.

Модели математического программирования (планирования) включают модели линейного программирования, нелинейного программирования, динамического программирования. Сюда же обычно относят и модели сетевого планирования.

Математическое программирование объединяет ряд математических методов, предназначенных для наилучшего распределения имеющихся в наличии ограниченных ресурсов – сырья, топлива, рабочей силы, времени, а также для составления соответствующих наилучших (оптимальных) планов действий.

К вероятностным моделям относятся модели, построенные с помощью аппарата теории вероятностей, модели случайных процессов марковского типа (марковские цепи), модели теории массового обслуживания и др.

Вероятностные модели описывают явления и процессы случайного характера, например связанные со всевозможными несистематическими отклонениями и ошибками (производственный брак и др.), влиянием стихийных явлений природы, возможными неисправностями оборудования и т. п.

К статистическим моделям относятся модели последовательного анализа, метода статистических испытаний (Монте-Карло) и др. Сюда же можно отнести и методы случайного поиска.

Метод статистических испытаний заключается в том, что ход той или иной операции проигрывается, как бы копируется с помощью ЭВМ, со всеми присущими данной операции случайностями, например при моделировании организационных задач, сложных форм кооперации различных предприятий и т. п. Применение данного метода называют имитационным моделированием.

Методы случайного поиска применяются для нахождения экстремальных значений сложных функций, зависящих от большого числа аргументов. В основе этих методов лежит использование механизма случайного выбора аргументов, по которым осуществляется минимизация. Методы случайного поиска находят применение, например, при моделировании организационных структур управления.

Теоретико-игровые модели предназначены для обоснования решений в условиях неопределенности, неясности (неполноты информации) обстановки и связанного с этим риска. К теоретико-игровым методам относятся теория игр и теория статистических решений.

Теория игр – это теория конфликтных ситуаций. Она применяется в тех случаях, когда неопределенность обстановки вызывается возможными действиями конфликтующих сторон.

Теоретико-игровые модели могут найти применение при обосновании управленческих решений в условиях производственных, трудовых конфликтов, при выборе правильной линии поведения по отношению к заказчикам, поставщикам, контрагентам и т. п.

Теория статистических решений применяется тогда, когда неопределенность обстановки вызывается объективными обстоятельствами, которые либо неизвестны (например, некоторые характеристики новых материалов, качества новой техники и т. п.), либо носят случайный характер (состояние погоды, возможное время выхода отдельных узлов изделия из строя и т. п.).

Теоретико-игровые модели целесообразно использовать при подготовке, проведении и оценке результатов деловых игр.

Все математические модели могут быть подразделены также на модели оценки эффективности и модели оптимизации.

Модели оценки эффективности предназначены для выработки характеристик производства и управления. К этой группе относятся все вероятностные модели. Модели оценки эффективности являются «входными» по отношению к моделям оптимизации.

Модели оптимизации предназначены для выбора наилучших в данных условиях способов действий или линии поведения. К этой группе относятся экстремальные и статистические модели, модели математического программирования, а также теоретико-игровые модели.

Ниже будут рассмотрены некоторые наиболее распространенные модели, применяемые при решении производственных задач, а также для формирования организационных структур управления производством.

Основным направлением моделирования управления производственно-экономическими системами является создание моделей управления производством.

В настоящее время разработаны и находят применение модели следующих функций управления производством:

– планирования производственно-экономической деятельности предприятия;

– оперативного управления;

– оперативного регулирования;

– управления материально-техническим снабжением производства;

– управления сбытом готовой продукции;

– управления технической подготовкой производства.

Разработана также система взаимосвязанных моделей производства и управления.

Модели планирования производственно -экономической деятельности предприятия. Целевая функция моделей этой группы предусматривает:

– максимизацию критерия эффективности производственной деятельности предприятия исходя из наличных мощностей и отпускаемых ресурсов;

– минимизацию расхода ресурсов в рамках заданного критерия эффективности.

Модели планирования производственной деятельности предприятия подразделяются на: модели прогнозирования, модели технико-экономического планирования, модели оперативно-производственного планирования.

Модели прогнозирования представляют собой модели, либо основанные на математических методах (наименьших квадратов, пороговых значений, экспоненциального сглаживания), либо на методах экспертных оценок.

Модели технико-экономического планирования базируются на методах математического программирования (планирования). В качестве основного критерия эффективности (целевой функции) при выработке оптимального плана обычно избираются конечные результаты производства, например величина прибыли. В качестве ограничений берутся ограничения по сложности выпускаемой продукции, времени работы оборудования, ресурсам и т.д. Поскольку величина некоторых из указанных ограничений носит случайный характер (например, время работы оборудования), при решении таких задач оптимизации применяется вероятностный подход. Типовыми оптимизационными моделями технико-экономического планирования являются модели для расчета оптимального плана, распределения производственной программы по календарным периодам, оптимальной загрузки оборудования. Эти модели строятся с помощью математических методов оптимизации.

Модели оперативно-производственною планирования обычно совмещаются с моделями оперативного управления.

Модели оперативного управления. Основными задачами оперативного управления являются оперативно-календарное планирование производства, систематический учет и контроль за выполнением календарных планов, а также оперативное регулирование хода производства.

Типовыми моделями оперативного управления являются модели для расчета оптимального размера партий изделий и расчета оптимального графика запуска-выпуска партий деталей (календарное планирование).

Модели для расчета оптимального размера партий изделий могут быть созданы применительно как к простой, так и полной постановке задачи. В простой постановке определение размера производства или закупки партии деталей, при котором годовые затраты оказываются минимальными, сводится к обычной задаче на отыскание минимума функции. В полной постановке отыскивается такая совокупность размеров партий, которой соответствуют минимальные суммарные затраты на переналадку оборудования и отчисления на незавершенное производство при ограничениях по длительности переналадок, ресурсам оборудования, взаимозависимости размеров партий на смежных операциях и обеспечению занятости рабочего. Решение этой задачи достигается с помощью математических методов оптимизации.

Модели для расчетов календарного планирования могут быть:

– статистические с оптимизацией методом случайного поиска;

– имитационные с набором правил предпочтения;

– эвристические, применяемые в тех случаях, когда невозможно создание строгих алгоритмов, но есть необходимость использовать информацию и оценить факты, не имеющие количественного выражения.

Модели оперативного регулирования. Эти модели имеют целью обеспечить удержание отклонения результатов производственной деятельности от плановых показателей в заданных пределах. В этомслучае применяются модели двух типов: модели регулирования по критериюоптимальности, модели регулирования по отклонению.

Модели регулирования по критерию оптимальности основываются на том, что после конкретного замера фактического состояния процесса производства составляется план, оптимальным образом приводящий процесс к заранее намеченному состоянию на момент окончания периода планирования.

Модели регулирования по отклонению базируются на том, что после конкретного замера производственный процесс в кратчайший срок выводят на первоначально составленный план-график.

Построение обеих моделей осуществляется с помощью математического аппарата оптимизации, применяемого в теории автоматического регулирования.

Модели управления материально-техническим снабжением производства. В качестве центральной проблемы управления материально-техническим снабжением производства выступает задача определения необходимого объема запасов всех видов снабжения. При этом могут быть построены две принципиально отличающиеся модели управления запасами – с фиксированным размером заказа и с фиксированным уровнем запасов. Существует также промежуточная модель, в которой фиксируется как верхний уровень запасов, так и нижний уровень заказа.

Построение моделей управления материально-техническим снабжением осуществляется с помощью специальных математических методов оптимизации, которые получили название «теория управления запасами».

Модели управления сбытом готовой продукции. Главной проблемой управления сбытом готовой продукции является задача расчета годового плана поставок готовой продукции. Для решения этой задачи с помощью математических методов оптимизации строится оптимизационная модель годового плана поставок готовой продукции. В качестве целевой функции при этом выступает стоимость реализованной продукции, в качестве ограничений – требование, чтобы суммарный объем продукции, отгруженной в определенный интервал времени всем потребителям, не превышал объема выпуска продукции за то же время, а суммарный объем поставок потребителю за все временные интервалыне превышал месячной заявки.

Модели управления технической подготовкой производства. Техническая подготовка производства включает стадии конструкторской и технологической подготовки.

С помощью математического моделирования могут быть решены три основные задачи управления технической подготовкой производства:

– определение минимального срока выполнения комплекса мероприятий технической подготовки производства при ограничениях на уровень наличных ресурсов;

– определение минимальной стоимости выполнения комплекса мероприятий технической подготовки производства при ограничениях на сроки его выполнения и на уровень наличия ресурсов;

– определение минимального уровня потребления дефицитных ресурсов при ограничении на стоимость и на сроки выполнения мероприятий технической подготовки производства.

Процесс технической подготовки производства наиболее полно и удобно воспроизводит сетевая модель. Сетевая модель дает возможность учесть вероятностный характер таких основных параметров операций технической подготовки производства, как длительность выполнения работ и интенсивность потребления ресурсов.

Оптимизация достигается применением методов математического программирования (в частности, симплекс-метода) и случайного (статистического) поиска.

Наряду с рассмотренными отдельными моделями, реализующими основные функции управления процессом производства, существует и система взаимосвязанных моделей производства и управления. Сущность этой системы моделей, построенной с помощью математического аппарата теории множеств, теории графов и повторного исчисления, заключается в следующем. В качестве множеств рассматриваются множество изделий, выпускаемых предприятием, и множество используемых при этом ресурсов. Производственный процесс, обеспечивающий выпуск множества изделий, описывается совокупным графом, а технологический процесс производства отдельного изделия – его конструкторско-технологическим графом. Множество ресурсов, обеспечивающих производство, состоит из подмножеств ресурсов рабочей силы, оборудования и дефицитных комплектующих изделий и материалов. Состояние производства на любой момент времени может при этом быть описано вектором, представляющим собой совокупность готовых изделий, полуфабрикатов и деталесборочных единиц, выпущенных к этому моменту. Аналогично с помощью вектора определяется и состояние ресурсов на любой момент времени. Плановая траектория производственного процесса при этом будет описываться вектор-функцией.

При такой постановке задачи оптимальное управление предприятием в плановый период может быть найдено исходя из следующего требования: на множестве допустимых планов, определяемых вектор-функцией, найти такой план, который максимизирует прибыль при условии, что вероятность его выполнения и получения прибыли установленного уровня будет не меньше заданного уровня, а затрачиваемые ресурсы не превысят имеющихся в наличии.

Моделирование организационных структур управления имеет целью совершенствование, оптимизацию системы управления предприятием. Оно является необходимым предварительным шагом автоматизации управления производственно-экономическими системами, которая требует серьезной подготовительной работы.

В качестве математического аппарата моделирования организационных структур управления применяется теория массового обслуживания. При этом элементы системы массового обслуживания принимаются как элементы системы управления, каждый из которых предназначен для решения определенной управленческой задачи. Для всех задач – элементов предусматривается система приоритетов в очередности решения. Для каждой задачи известны также и характеристики входящих потоков требований на обслуживание – решение соответствующих задач управления.

Элемент системы управления, решающий ту или иную задачу, располагает одним или несколькими преобразователями информации, в качестве которых выступают либо специалисты определенной квалификации, либо технические средства.

Эффективность работы системы управления оценивается по качеству и длительности обслуживания решения задач управления, с учетом их приоритетов и сложности.

Моделирование систем массового обслуживания может выполняться как аналитическими, так и статистическими методами. Наибольшее применение при моделировании организационных структур управления получил статистический метод, так называемый метод статистических испытаний (метод Монте-Карло). Этому методу отдается предпочтение на том основании, что он позволяет решать задачи большой сложности, для которых не существует аналитического (формульного) описания или последнее обладает чрезвычайной сложностью.

Статистическая модель позволяет поставить математический эксперимент, аналогичный натурному, произвести имитацию организационной структуры управления наиболее дешевым способом и в приемлемое время. Вместе с тем необходимо учитывать и специфические недостатки метода статистических испытаний, из которых главными являются относительно большое время моделирования и частный характер получаемых решений, определяемый фиксированными значениями параметров системы массового обслуживания.

При моделировании с помощью математического аппарата теории массового обслуживания структура системы управления предприятием рассматривается как совокупность взаимосвязанно функционирующих элементов. Такими элементами в реальной системе являются дирекция и функциональные отделы управления: производственно-технический, плановый, снабжения и др.

В результате совместного функционирования указанных элементов в системе управления осуществляется преобразование информации состояния в командную информацию, являющуюся основой управления предприятием.

Упомянутые элементы – подразделения системы управления предприятием составляют цепь, анализ функционирования которой может быть достаточно формализован с целью оптимизации процесса управления. Простейшей цепью, дающей хорошее приближение к реальности, является строго последовательная цепь элементов. При моделировании такой цепи возможны два похода: квазирегулярное и случайное представление. В квазирегулярной модели моделирование осуществляется по каждому элементу отдельно по усредненным показателям.

В случайной модели рассчитываются статистические оценки для каждого запроса на обслуживание, проходящего не по отдельным элементам, а по системе в целом.

Наряду с моделированием организационных структур управления с помощью цепей элементов существует способ математического описания оргструктуры системы управления с помощью линейных стохастических сетей, являющихся одним из классов многофазных систем массового обслуживания. В данной модели информация также проходит последовательно через ряд элементов системы управления, каждый из которых описывается с помощью математического аппарата теории массового обслуживания. При последовательном прохождении информации через элементы сети имеют место переходы марковского типа. Структура такой сети с соответствующими переходами представляется определенным графом. Составляется стохастическая матрица переходов.

Поскольку целевая функция (критерий эффективности) при математическом моделировании организационных структур управления, как правило, может быть описана лишь статистически, оптимизация производится в основном численными методами, из которых наибольшее применение получили методы динамического программирования и статистического поиска.

Решение задачи оптимизации методом динамического программирования реализуется путем составления для каждого шага процесса управления функционального рекуррентного уравнения (уравнения Беллмана).

Оптимизация организационных структур управления с помощью метода статистического поиска, несмотря на менее жесткие ограничения, накладываемые на критерии эффективности и допущения, описывающие физику явления при данном методе, пока не получила, применительно к рассматриваемой задаче, достаточно широкого распространения.

Игровое моделированиезанимает особое место в ряду методов, применяемых для автоматизации управления производственно-экономическими системами. Отличительная черта этого метода – привлечение для моделирования процесса управления людей, участвующих в разработке и проведении деловой игры. Под деловой игрой при этом понимается имитация группой лиц решения отдельных задач хозяйственной или организационной деятельности предприятия, выполняемая на модели объекта в обстановке, максимально приближенной к реальной.

Введение в модель человека как элемента организации управления дает возможно учесть его поведение в тех случаях, когда оно не может быть адекватно описано с помощью известных сегодня математических моделей; позволяет решать такие управленческие задачи, которые не укладываются в рамки существующих формализованных методов.

Деловая игра вводит в процесс подготовки и принятия управленческих решений психологические и эмоциональные моменты, поощряя использование в этом процессе прошлого опыта руководителей, их интуиции, развивая способность к эвристическим решениям. Деловая игра проводится применительно к определенной управленческой задаче по заранее тщательно разработанному сценарию. Общая игровая модель формируется как совокупность частных моделей, создаваемых участниками – лицами, готовящими и принимающими управленческие решения.

Модель деловой игры включает как формализованную, так и неформализованную часть. Участники игры действуют по определенным правилам. Они руководствуются специально разработанными инструкциями по ведению игры, а также поступающими в их распоряжение данными обстановки.

В соответствии со сценарием игры участники периодически получают вводные об изменении обстановки. Готовя свои решения, участники деловой игры оценивают обстановку и производят необходимые расчеты вручную или с помощью ЭВМ. При этом используются формализованные, заготовленные заранее элементы игровой модели, соответствующие современным методам исследования операций.

Осуществляя управление ходом деловой игры, ее руководитель оценивает решения участников, устанавливает результаты их действий и доводит последние до играющих. При необходимости руководитель игры может менять установку, доводя эти изменения до участников в виде вводных. Оценка действий участников игры производится путем расчетов, экспертными методами, а также исходя из опыта руководителя, его интуиции и здравого смысла.

Основным видом игрового моделирования, проводимого на предприятиях, является производственная деловая игра. Ее цель – совершенствование существующих и выработка новых форм организации управления производством, отработка руководящих документов, перестройка производства и т. д.

В качестве моделей при проведении деловых игр широко применяются методы сетевого планирования и управления (СПУ), построенные на основе сетевых графиков. При решении задач планирования находят применение методы динамического программирования, а при решении задач распределения ресурсов – линейного программирования.

Для обучения управленческого персонала производственная деловая игра может проводиться в учебном варианте, т. е. учебная деловая игра. Ее главной задачей является обучение работников, совершенствование их навыков в управлении. При необходимости учебная деловая игра используется и для аттестования руководящих работников предприятий в выполнении ими своих должностных обязанностей, а также при выдвижении их на высшую должность.