Пояснения к лабораторной работе.
Как известно из теории, для облегчения анализа различных режимов работы трансформатора используется так называемая Т-образная схема замещения (рис.4.1.а.). На ней величины r1 и r'2 обусловлены, в основном, омическими сопротивлениями фаз первичной и приведённой вторичной обмоток, х1 и х'2 - потоками рассеяния этих обмоток, rμ - сопротивление, потери в которомравны потерям на перемагничивание стали трехфазного трансформатора, хμ - индуктивное сопротивление, обусловленное потоком взаимоиндукции, падение напряжения на котором целесообразно
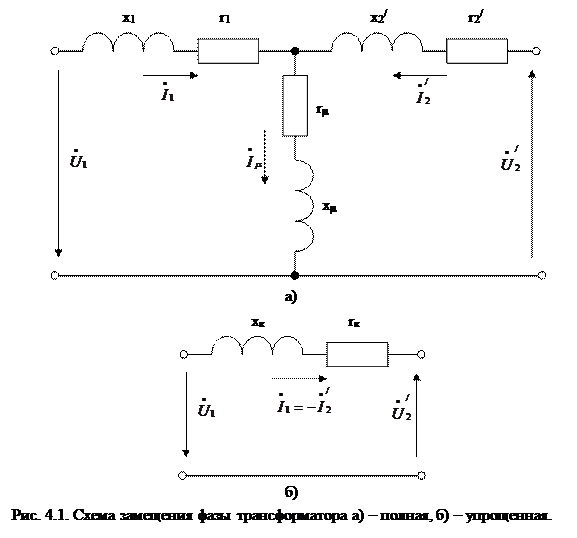 |
представлять в виде ЭДС взаимоиндукции, передаваемой из первичной цепи во вторичную цепь трансформатора.
Так как ток намагничиванияIμ у силовых трансформаторов составляет обычно несколько процентов от номинального тока Iн, во многих инженерных расчётах этой величиной пренебрегают,в результате чего схема замещенияупрощается, принимая приведённый на рисунке 4.1.б. вид. На этой схеме величины  и
и 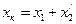 - соответственно, активное и индуктивное сопротивления короткого замыкания.
- соответственно, активное и индуктивное сопротивления короткого замыкания.
Для определения параметров схемы замещения проводятся два опыта: опыт холостого хода и опыт короткого замыкания.
Схема опыта холостого хода представлена на рисунке 4.2.а.
 По данным этого опыта с достаточной для инженерных расчетов точностью можно найти коэффициент трансформации К12:
По данным этого опыта с достаточной для инженерных расчетов точностью можно найти коэффициент трансформации К12:
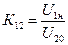 . .
| (4.1) |
гдеU1н - номинальное напряжение на первичной обмотке трансформатора, U20 – напряжение на вторичной обмотке в опыте холостого хода.
Известно, что точное значение коэффициента трансформации вычисляется по формуле
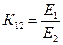 , ,
| (4.2) |
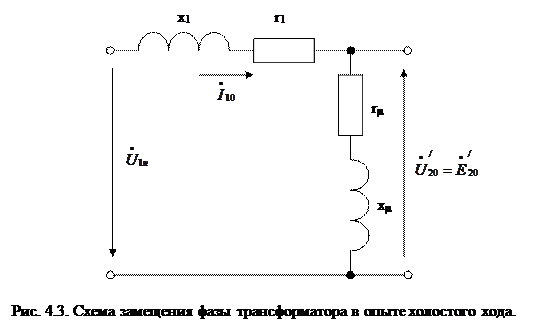 |
где Е1 и Е2 – ЭДС первичной и вторичной обмоток в любом режиме работы трансформатора. На рисунке 4.3 показано, что в режиме холостого хода, когда падения напряжения на сопротивлениях r'2 и х'2 отсутствуют, измеряемое на вторичной стороне напряжение и есть ЭДС Е20 (индекс "0" означает режим холостого хода). Напряжение U1н больше ЭДС Е10 на падения напряжения в сопротивлениях r1 и х1 от тока холостого хода I10. Этот ток составляет несколько процентов от номинального тока первичной обмотки, и падения напряжения от него, действительно, пренебрежимо малы. Это значит, что данные, полученные в опыте холостого хода, позволяют с высокой точностью определить коэффициент трансформации трансформатора.
Как видно из рисунка 4.3, активная мощность, потребляемая трансформатором в опыте холостого хода, есть мощность, выделяющаяся в сопротивлениях r1 и rμ. Обозначив сумму этих сопротивлений за r0, можно вычислить ее как
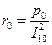 , ,
| (4.3) |
В связи с тем, что величина r1 пренебрежимо мала по сравнению с rμ, можно считать, что 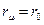 , и вся потребляемая в опыте холостого хода активная мощность р0 идет на нагрев сердечника.
, и вся потребляемая в опыте холостого хода активная мощность р0 идет на нагрев сердечника.
Индуктивную составляющую 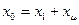 можно определить из полного сопротивления
можно определить из полного сопротивления
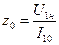
| (4.4) |
по формуле
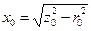 . .
| (4.5) |
Принимая во внимание, что сопротивление хμ, у силовых трансформаторов на несколько порядков больше сопротивления х1, можно считать, что 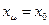 .
.
Необходимо помнить, что вследствие насыщения сердечника зависимость междуU1 и током холостого хода I10 нелинейна, поэтому и сопротивления rμи xμ также зависят от величины U1. Для использования в схеме замещения эти величины должны определяться при номинальном значении первичного напряжения U1н.
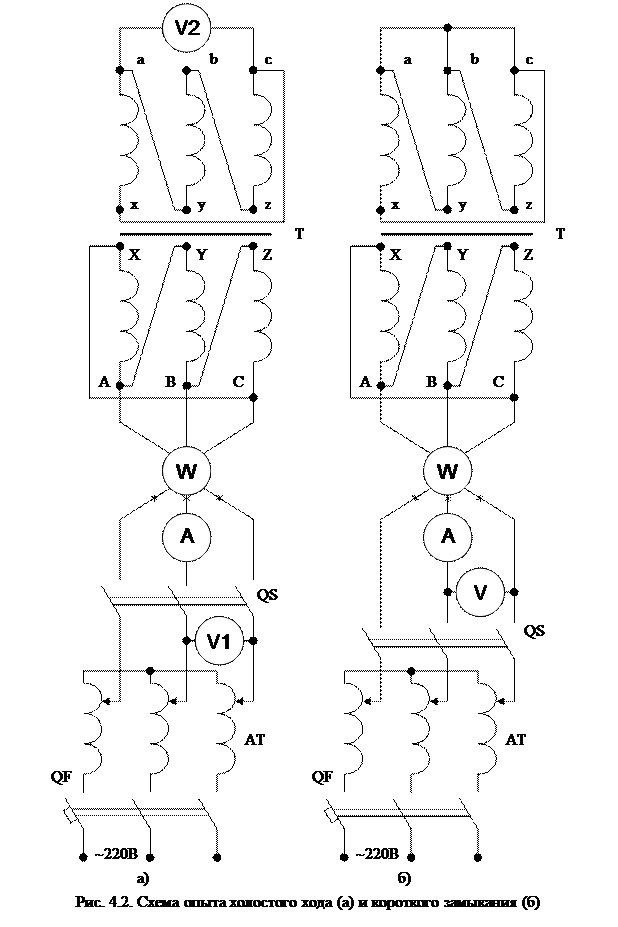
В опыте короткого замыкания (рис. 4.2.б) по обмоткам трансформатора текут номинальные токи, которые нагревают проводники обмоток так же, как в номинальном режиме работы. Но, в отличие от номинального режима, первичное напряжение трансформатора в этом опыте составляет менее 10% номинала, значит, магнитными потерями, зависящими от действующего значения напряжения, можно пренебречь.
Об этом же свидетельствует схема замещения, соответствующая опыту короткого замыкания (рис. 4.4): из-за известного соотношения между сопротивлениями rμ и rк, ток, ответвляющийся в ветвь намагничивания, пренебрежимо мал, по сравнению с током текущим в короткозамкнутой ветви, то есть мощность, выделяющуюся в сопротивлении rμ, можно считать равной нулю.
Небольшая часть мощности, потребляемой трансформатором в этом опыте, идет, также, на нагрев защитного кожуха, стяжных болтов и других металлических деталей, по которым замыкаются потоки рассеяния трансформатора.
Пренебрегая всеми потерями, кроме электрических, можно считать, что мощность, потребляемая в опыте короткого замыкания, равна
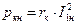 . .
| (4.6) |
 |
Индекс "н" в обозначении мощности короткого замыкания означает, что опыт проводится при номинальных токах обмоток.
Используя формулу (4.6), легко найти активное сопротивление короткого замыкания, которое разделяется на первичную и вторичную составляющие следующим образом:
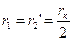 . .
| (4.7) |
Для вычисления полного сопротивления короткого замыкания необходимо воспользоваться законом Ома:
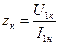 . .
| (4.8) |
Индуктивное сопротивление короткого замыкания
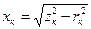 . .
| (4.9) |
разделяется на первичную и вторичную составляющие так же, как активное сопротивление:
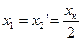 . .
| (4.10) |
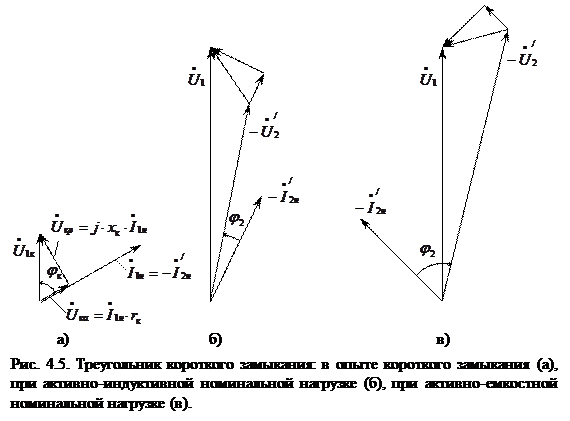 |
Величина U1к в формуле (4.8), именуемая "напряжением короткого замыкания", является важной характеристикой трансформатора. Это действующее значение питающего напряжения, обеспечивающее в режиме короткого замыкания протекание в обмотках трансформатора номинальных токов. По рисунку 4.4 видно, что эта величина может быть, также, определена как падение напряжения от номинального тока на полном сопротивлении короткого замыкания. То есть, напряжение короткого замыкания характеризует неизбежное изменение напряжения в трансформаторе при его работе под нагрузкой, обусловленное наличием активного сопротивления проводников обмоток и существованием потоков рассеяния. При работе трансформатора в номинальном режиме падение напряжения на внутренних сопротивлениях rки xк будет таким же, как в опыте короткого замыкания. На рисунке 4.5 показано, как, используя упрощенную схему замещения трансформатора (рис. 4.1.б) и треугольник короткого замыкания, можно строить векторные диаграммы для любого режима работы трансформатора. При отличии тока нагрузки от номинального значения, стороны треугольника изменяются пропорционально.
Из рисунка 4.5.а видно, что активная и реактивная составляющие напряжения короткого замыкания могут быть вычислены, соответственно, как
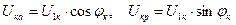 , ,
| (4.11) |
где
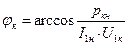 . .
| (4.12) |
Как правило, напряжение короткого замыкания и его составляющие представляют в виде относительных величин: в долях номинального напряжения первичной обмотки:
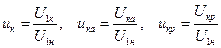 , ,
| (4.13) |
или в процентах
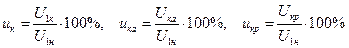 . .
| (4.14) |
Такое представление напряжения короткого замыкания наиболее целесообразно, так как в ходе опыта оно определяется как напряжение первичной обмотки, а используется в дальнейшем для вычисления вторичного напряжения.
Полученные составляющие напряжения короткого замыкания позволяют строить внешние характеристики трансформатора, не загружая его. В данной работе предлагается строить внешние характеристики в относительных единицах, то есть
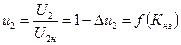 при при 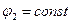 , ,
| (4.15) |
где Dи2 – относительное изменение напряжения – при нагрузках трансформатора, не превышающих номинальные, может быть определено по упрощенной формуле:
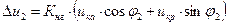 , ,
| (4.16) |
в которой 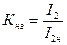 - коэффициент нагрузки трансформатора.
- коэффициент нагрузки трансформатора.
Как видно из рисунков 4.5.б и 4.5.в, при увеличении нагрузки трансформатора его вторичное напряжение может, как уменьшаться, так и расти. При активно-индуктивной нагрузке – рисунок 4.5.б – вторичное напряжение под нагрузкой меньше, чем на холостом ходе, при значительной доли емкости в нагрузке трансформатора – рисунок 4.5.в – напряжение оказывается выше, чем при работе вхолостую. Это значит, что изменение напряжения может быть как положительным, так и отрицательным, а внешняя характеристика может иметь как ниспадающий, так и восходящий вид. Для получения корректных результатов при использовании формулы (4.16) необходимо учитывать знак угла нагрузки, отсчитываемого от вектора тока I2' в направлении вектора напряжения U2': этот угол положительный, если нагрузка активно-индуктивная и отрицательный, если нагрузка активно-емкостная.
Полученные в ходе опытов холостого хода и короткого замыкания данные могут использоваться для определения КПД трансформатора в любом режиме работы:
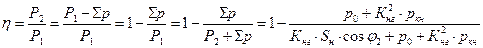 , ,
| (4.17) |
где Sр – суммарные потери, состоящие из неизменных магнитных потерь (потерь холостого хода) р0 и зависящих от квадрата тока электрических потерь (пропорционально измененных потерь опыта короткого замыкания) Кнг2×ркн, Sн – номинальная полная мощность трансформатора, измеряемая в ВА. С помощью формулы (4.17) могут быть построены зависимости КПД трансформатора от коэффициента нагрузки при неизменных значениях угла нагрузки.
 Как было показано выше, в зависимости от коэффициента мощности внешняя характеристика в области рабочих нагрузок может иметь различный наклон, ниспадающий и восходящий вид. При значительном – неноминальном и аварийном – увеличении нагрузки, независимо от ее характера, вторичное напряжение трансформатора снижается, и все внешние характеристики сходятся в одной точке на оси абсцисс (рис. 4.6). При коротком замыкании вторичной обмотки наибольший интерес представляет рассмотрение трансформатора как нагрузки для питающей сети, то есть, рассмотрение потребляемого из сети тока I1. В этой связи следует различать установившийся ток короткого замыкания I1к и, так называемый, ударный ток короткого замыкания I1уд.
Как было показано выше, в зависимости от коэффициента мощности внешняя характеристика в области рабочих нагрузок может иметь различный наклон, ниспадающий и восходящий вид. При значительном – неноминальном и аварийном – увеличении нагрузки, независимо от ее характера, вторичное напряжение трансформатора снижается, и все внешние характеристики сходятся в одной точке на оси абсцисс (рис. 4.6). При коротком замыкании вторичной обмотки наибольший интерес представляет рассмотрение трансформатора как нагрузки для питающей сети, то есть, рассмотрение потребляемого из сети тока I1. В этой связи следует различать установившийся ток короткого замыкания I1к и, так называемый, ударный ток короткого замыкания I1уд.
Если в опыте короткого замыкания напряжение на первичной обмотке специально снижается таким образом, чтобы токи трансформатора не превышали номинальных значений, то при внезапном (аварийном) коротком замыканииU1может остаться близким кU1н. Тогда установившийся ток короткого замыкания первичной обмотки I1к может быть найден из пропорции:
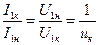 . .
| (4.18) |
То есть, напряжение короткого замыкания является, кроме прочего, характеристикой, определяющей величину установившегося тока короткого замыкания. Если, например, 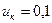 (или 10%), то
(или 10%), то 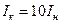 .
.
Ударный ток короткого замыкания определяется выражением
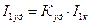 , ,
| (4.19) |
где
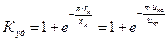 – –
| (4.20) |
ударный коэффициент, который также может быть найден с помощью данных, полученных в опыте короткого замыкания.
Важно! При расчете параметров схемы замещения и других величин, характеризующих трехфазный трансформатор, следует помнить, что в приведенные выше расчетные формулы необходимо подставлять значения токов, напряжений и мощностей, приходящиеся на фазу трансформатора. В том случае, если электроизмерительный прибор измеряет линейное значение электрической величины или значение, приходящееся на все три фазы, нужно предварительно, используя известные из курса электротехники соотношения, вычислить фазные значения.
Дата добавления: 2015-03-20; просмотров: 865;
