Представление о шаре, его элементах.

Про такие предметы, как арбуз, мяч, глобус, гово­рят, что они имеют форму шара (рис. 7).

рис. 7

Представим, что полукруг вращается вокруг диаметра АВ (рис. 8). Тогда образуется фигура, которую называют шаром.

При вращении полукруга образуется поверхность шара — фигура, которую называют сферою. Сфера ограничивает шар.

рис. 8

Центр, диаметр, радиус полукруга — это соответственно центр, диаметр, радиус шара и сферы, которая его ограничивает.

Наверне, вам приходилось видець, карк для приготовлення еды нарезают овощи и фрукты. От направления разреза зависит форма сечения (рис. 9). Шар отличается тем, что его сечением плоскостью всегда является круг (рис. 10). Если плоскость сечения проходит через центр шара, то в сечении образуется круг, радиус которого равен радиусу шара (рис. 11).

рис. 9

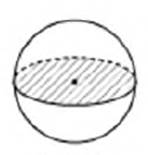
рис. 10 рис. 11

В 5 классе вы познакомились с отдельным видом гео­метрических тел — многогранниками. Другим отдельным видом геометрических тел являются тела вращения. Цилиндр, конус и шар — примеры тел вращения.

Начертить фигуры в тетради и подписать их элементы:

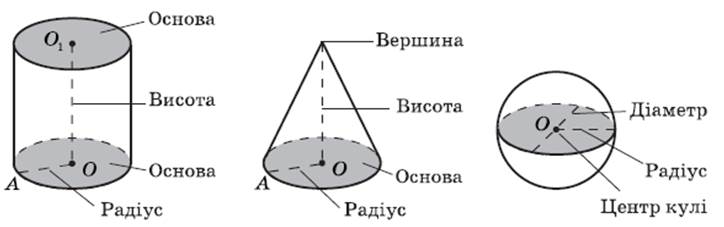
Решение задач

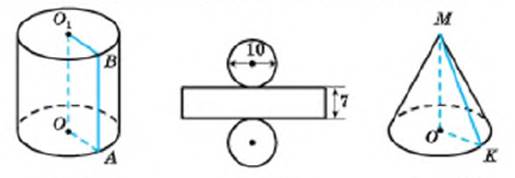
рис. 12 рис. 13 рис. 14

№ 1. На рисунке 12 изображен цилиндр. Укажите:

1) Образующую цилиндра;

2) радиус нижнегооснования цилиндра;

3) радиус верхнего основания цилиндра.

Решение

1) образующая цилиндра – АВ;

2) радиус нижнего основания цилиндра – ОА;

3) радиус верхнего основания цилиндра - О₁В.

№ 2. Радиус основания цилиндра 6 см, а его образующая 8 см. Найти площадь боковой поверхности цилиндра.

Решение

S_бок = 2πR•h

=2•3,14•6•8 ≈ 301,44 (см²) - площадь боковой поверхности цилиндра.

Ответ: 301,44 см².

№ 3. На рисунке 14 изображен конус. Укажите:

1) вершину конуса;

2) центр его основания;

3) образующую конуса;

4) радиус основания конуса;

5) висоту конуса.

Решение

1) вершина конуса – т. М;

2) центр его основания – т. О;

3) образующая конуса – МК;

4) и 5) выполнить самостоятельно.

№ 4. Радиус шара равен 6 см. Найдите площадь сечения шара плоскостью, которая проходит через центр шара.

Один из возможных вариантов рисунков к этой задаче:

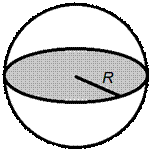
Решение

Сечением плоскостью шара всегда является круг, поэтому найдем площадь этого круга.

S = π • R²

3,14•6² ≈ 3,14•36 ≈ 113,04 (см²) – площадь сечения шара

Ответ: 113, 04 см².

Домашнее задание

Учить теоретический материал по теме. Письменно выполнить № 5, № 6, № 7.

№ 5. Найти площадь боковой поверхности цилиндра, развертка которого изображена на рисунке 13 (длины отрезков даны в сантиметрах).

№ 6. Длина окружности, которая ограничивает сечение шара плоскостью, которая проходит через ее центр, равна 12,56 см. Чему равен радиус шара?

№ 7. Какие наименьшие размеры, выраженые целым числом сантиметров, должен иметь прямоугольный лист бумаги, чтобы ним можно было обклеить боковую поверхность цилиндра с радиусом основания 5 см и высотой, которая равна диаметру основания?