Капиллярная постоянная.

Если открытую с обеих сторон цилиндрическую капиллярную трубку радиусом rопустить в сосуд с жидкостью, которая полностью смачивает стенки трубки, то жидкость в трубке поднимется на высоту h, которая определится из формулы (17.2.1)

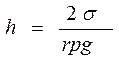, (17.2.1)

где р - плотность жидкости;

g- ускорение свободного падения.

Если жидкость не смачивает стенки трубки, то уровень ее в трубке будет стоять ниже, чем в широком сосуде, на величину, определяемую по формуле (17.2.2).

Величина 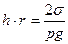- не зависит от радиуса капилляра и определяется молекулярной природой жидкости, в связи с чем называется капиллярной постоянной. Капиллярная постоянная измеряется в квадратных миллиметрах и численно равна высоте капиллярного поднятия в полностью смачиваемой трубке радиусом 1 мм.

В ареометрии принято называть капиллярной постоянной величину 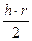условно обозначаемую буквой а, которая вычисляется по формуле (17.2.2)

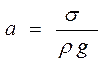, (17.2.2)

Для получения капиллярной постоянной, выраженной в квадратных миллиметрах, необходимо умножить на 100 значение, найденное по формуле (17.2.2), где 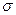выражено в дин/см, р - в г/см³, g - в см/с².

Капиллярная постоянная с повышением температуры уменьшается; исключение составляют растворы глицерина в воде: при содержании глицерина свыше 60 % капиллярная постоянная растет по мере нагревания раствора.

Рассмотренные выше капиллярные явления приобретают особенное значение при ареометрических измерениях. Вокруг стержня ареометра, плавающего в жидкости, поверхность искривляется и образуется вогнутый мениск (искривление поверхности в месте прикосновения со стержнем ареометра с жидкостью), так как большинство жидкостей смачивает стекло. Мениск как бы прилипает к стержню ареометра, увеличивая его массу, отчего ареометр погружается в жидкость на большую глубину; здесь и далее объем жидкости между мениском и горизонтальной плоскостью, касательной к нему, условно именуется мениском.

Мениск, представляющий собой некоторое количество жидкости, поднявшейся вдоль стержня ареометра, удерживается силой поверхностного натяжения, которое действует на линии соприкосновения жидкости со стержнем.

В случае полного смачивания стержня ареометра жидкостью сила поверхностного натяжения направлена вдоль стержня и равна произведению поверхностного натяжения 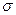на длину окружности стержня, т.е. 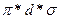, где d - диаметр стержня. Обозначая массу мениска через m, получаем следующее уравнение равновесия (17.2.3)

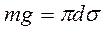, (17.2.3)

После подстановки значения 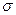из формулы (17.2.2) находим выражение для определения массы мениска, т.е. получаем формулу (17.2.4)

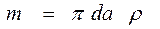, (17.2.4)

Хотя масса мениска сравнительно с массой ареометра весьма мала, подсчитаем, насколько погрузится ареометр под действием мениска.

Ареометр находится в равновесии в жидкости, когда его вес равен весу вытесненной жидкости; следовательно, вес жидкости в объеме той части стержня, которая погрузилась под действием мениска, ранен весу мениска.

Обозначим через , величину этой части стержня, запишем указанное условие в виде (17.2.5)

, (17.2.5)

откуда искомая глубина погружения ареометра будет вычисляться по формуле (17.2.6)

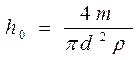, (17.2.6)

Как видим, под действием мениска ареометр погружается довольно значительно, так что влиянием мениска нельзя пренебречь.

Формулу (17.2.6) можно представить и в другом виде, если в нее подставить значение т из уравнения (17.2.4). Тогда получим формулу (17.2.7)

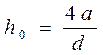, (17.2.7)

Формула (17.2.7) подтверждает, что в двух жидкостях, имеющих одинаковую плотность, но различную капиллярную постоянную, один и тот же ареометр даст разные показания. Если а₁ и а₂ - капиллярные постоянные жидкостей и а₁ >а₂ , то глубина погружения ареометра под действием мениска в первой жидкости будет больше, чем во второй, причем разность глубин согласно формуле (17.2.7) составит .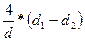

Таким образом, глубина погружения ареометра прямо пропорциональна капиллярной постоянной жидкости и обратно пропорциональна диаметру стержня ареометра. Отсюда следует, что в жидкости с большей капиллярной постоянной из-за большего погружения ареометр будет показывать меньшую, чем следует, плотность, так как значения плотности на шкале ареометра растут сверху вниз.

Уравнение равновесия ареометра в жидкости.

Рассмотрим силы, действующие на ареометр, плавающий в жидкости, и выведем уравнение равновесия ареометра, устанавливающее зависимость между основными размерами ареометра и плотностью жидкости.

Введем следующие обозначения:

- р - плотность жидкости;

- а - капиллярная постоянная жидкости;

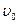- - объем всего ареометра;

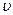- - объем корпуса ареометра и части стержня до нижнего штриха шкалы;

- l - расстояние от нижнего штриха шкалы до уровня жидкости;

- s - площадь поперечного сечения стержня;

- L - длина окружности сечения стержня;

- т - масса ареометра;

- D - плотность воздуха;

- g - ускорение свободного падения.

Для равновесия ареометра в жидкости необходимо, чтобы существовало равенство между силами, погружающими ареометр в жидкость, и силами, выталкивающими его из жидкости.

Допустим, что жидкость имеет ту температуру, для которой градуирован ареометр. Силы, погружающие ареометр в жидкость, складываются из веса ареометра 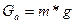и веса мениска 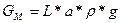(рисунок 17.2.3). Выталкивающая сила равна сумме следующих трех сил: веса жидкости в объеме погруженной части ареометра 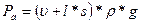; веса воздуха в объеме непогруженной части стержня 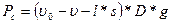; веса воздуха в объеме мениска [последний определяется делением массы мениска, на плотность жидкости] .

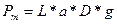Условие равновесия ареометра можно выразить в виде (17.2.8)

,

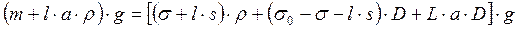или (17.2.8)

,

Принимая во внимание, что разность 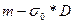представляет собой массу ареометра за вычетом массы воздуха в объеме ареометра, т.е. массу ареометра М, определенную взвешиванием в воздухе, получим следующее окончательное уравнение (17.2.9)

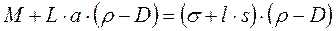, (17.2.9)

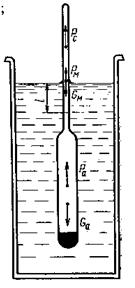
Рисунок 17.2.3 - Силы, действующие на ареометр

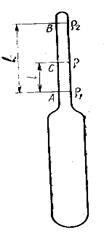
Рисунок 17.2.4 - Схема к расчету шкалы ареометра