Цвет и психика

Причина возникновения электрического тока в неподвижном проводнике - электрическое поле.
Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.Индукционное электрическое поле является вихревым. 
Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока
Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля

Первое уравнение Максвелла - это обобщение закона Ампера и Био-Саварра для токов смещения. Звучит следующим образом: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.

В современном обозначении записывается

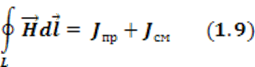
Т.о. физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области(токами смещения).

Это означает, что циркуляция вектора 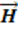по контуру L равна сумме токов проводимости и смещения.

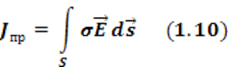
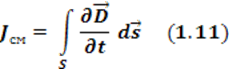
Подставляя 1.10, 1.11 в 1.9, получим

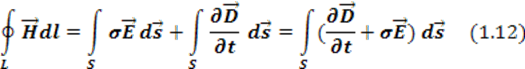
Уравнение 1.12 называют первым уравнением Максвелла в интегральной форме.

62)

Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения. Этот термин имеет смысл в таких веществах, как, например, диэлектрики. Там смещаются заряды под действием электрического поля. Но в вакууме зарядов нет – там смещаться нечему, а магнитное поле есть. То есть название Максвелла «ток смещения» – не совсем удачное, но смысл, вкладываемый в него Максвеллом, – правильный.

Максвелл сделал вывод: всякое переменное электрическое поле порождает переменное магнитное поле.

Токи проводимости в проводнике замыкаются токами смещения в диэлектрике или в вакууме. Переменное электрическое поле в конденсаторе создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий величину, равную току в металлическом проводнике.

Это утверждение позволяет (на базе нашего примера с конденсатором) найти величину тока смещения. В свое время мы с вами доказали, что поверхностная плотность поляризационных зарядов σ равна – вектору электрического смещения:

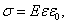
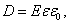
Полный заряд на поверхности диэлектрика и, следовательно, на обкладках конденсатора (S – площадь обкладки)

Тогда

т.е. ток смещения пропорционален скорости изменения вектора электрического смещения . Поэтому он и получил такое название – ток смещения.

Плотность тока смещения

Второе уравнение Максвелла- это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.

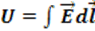(1.17)

Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.

Получим второе уравнение Максвелла в интегральной форме

Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.

63) система представляет собой второе уравнение Максвелла (см п.62) и

Четвертое уравнение Максвелла устанавливает отсутствие магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения

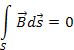
64) Система представляет собой первое уравнение Максвелла (см п.61) и

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора 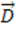через замкнутую поверхность S равен заряду Q, заключенному в данной поверхности:

где ρ – объемная плотность заряда.

Подставим 1.24 в 1.23, получим

Уравнение 1.25 есть третье уравнение Максвелла в интегральной форме.

Цвет и психика

В монографии освещаются различные аспекты взаимосвязи цвета и психики человека. Рассматривается история развития цветовой символики. Описывается психофизиологическое и психологическое воздействие цвета на человека. Анализируются факторы и механизмы цветовых предпочтений. Приводятся обширные данные об особенностях восприятия и отношение к цвету при шизофрении и других психических заболеваниях. Обсуждаются актуальные вопросы цветовой психодиагностики. Особое внимание уделяется цветовому тесту Люшера, как одной из наиболее распространенных методик цветовой психодиагностики. (Базыма Борис Алексеевич, кандидат психологических наук. — Цвет и психика. Монография. Харьков, 2001).

На зеленой траве — желтые одуванчики.
Обманщики!
Золота груды.
Подходи, пруды пруди.
Есть и изумруды.
Господи! За что такое искушенье?
На зеленой траве — желтые одуванчики.
Обманщики!