Инструкция GOTO

Инструкции if и case используются для выбора последовательности инструкций программы в зависимости от некоторого условия, поэтому их иногда называют инструкциями условного перехода. Помимо этих инструкций управления ходом выполнения программы существует еще одна — инструкция безусловного перехода goto.

В общем виде инструкция goto записывается следующим образом:

goto Метка

где метка — это идентификатор, находящийся перед инструкцией, которая должна быть выполнена после инструкции goto.

Метка, используемая в инструкции goto, должна быть описана в разделе меток программы, который начинается словом label и располагается перед разделом описания переменных.

Метка помечает какое-либо место в тексте программы. Метками могут быть числа от 0 до 9999 или идентификаторы, которые в этом случае уже нельзя использовать для каких-либо иных нужд. Все метки должны быть описаны в специальном разделе label:

Меткой может быть помечен любой оператор программы

В тексте программы метка ставится перед инструкцией, которая должна быть выполнена после инструкции goto. Сразу после метки ставится двоеточие.

Ниже приведена измененная процедура проверки простого числа, в которой для перехода к последней инструкции процедуры, в случае если пользователь введет неверные данные, используется инструкция goto.

procedure TForml.ButtonlClick(Sender: TObject);

label { раздел объявления меток } bye;

var

n: integer; { проверяемое число }

d: integer; { делитель }

r: integer; { остаток от деления n на d}

begin

n;=StrToInt(Editl.text) ;

if n <= 0 then begin

MessageDlg('Число должно быть больше нуля.', mtError,[mbOk],0) ;

Editl.text:= ' ';

goto bye;

end;

{ введено положительное число } d:= 2; { сначала будем делить на два }

repeat

r:= n mod d;

if r <> 0 { n не разделилось нацело на d } then d:= d + 1;

until r = 0;

label2.caption:=Editl.text ;

if d = n

then label2.caption:=label2.caption

+ ' простое число.' else label2.caption:=label2.caption

+ ' обычное число.' ;

bye:

end;

В литературе по программированию можно встретить суждения о недопустимости применения инструкции goto, так как она приводит к запутанности программ. Однако с категоричностью таких утверждений согласиться нельзя. В некоторых случаях использование goto вполне оправдано. Приведенный пример, когда goto используется для аварийного завершения процедуры, относится именно к таким случаям.

3. ОБЪЕКТЫ ИССЛЕДОВАНИЯ, ОБОРУДОВАНИЕ, МАТЕРИАЛЫ И НАГЛЯДНЫЕ ПОСОБИЯ

3.1. IBM – совместимый компьютер.

3.2. Установленная операционная система Windows.

3.3. Установленное приложение Borland Delphi.

3.4. Справочная система приложения Borland Delphi.

4. ЗАДАНИЕ НА РАБОТУ

4.1. Изучение теоретические положения работы по программированию в среде Borland Delphi.

4.2. Выполнение индивидуального задания преподавателя по программированию в пределах вопросов, рассмотренных в данной лабораторной работе.

5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

5.1. Ознакомиться с теоретическими положениями данной лабораторной работы.

5.2. Выполнить индивидуальное задание преподавателя по программированию (по заданиям приложения).

5.3. Оформить отчет по работе.

5.4. Защитить лабораторную работу путем ответа на вопросы преподавателя.

6. СОДЕРЖАНИЕ ОТЧЕТА

6.1. Описание цели работы.

6.2. Основные теоретические положения работы

6.3. Содержание индивидуального задания преподавателя по программированию.

6.4. Описание методики выполнения индивидуального задания.

7. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

7.1. Delphi 7 : [наиболее полное руководство] / А. Д. Хомоненко [и др.];под общ.ред.А.Д.Хомоненко .— СПб. : БХВ - Петербург, 2007 .— 1216с. : ил. (7 экз.)

7.2. Программирование в Delphi 7 / П. Г. Дарахвелидзе, Е. П.Марков .— СПб.: БХВ -Петербург, 2004 .— 784c. : ил. (1 экз.)

7.3 Осипов Д. Delphi. Профессиональное программирование. - СПб.: Символ-Плюс, 2006. -1056 с., ил.

ПРИЛОЖЕНИЕ

Индивидуальные задания

1. Циклические программы

1.1. Написать программу, позволяющую вычислить с помощью цикла:

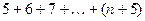, где n задается с клавиатуры.

1.2. Написать программу, позволяющую вычислить с помощью цикла:

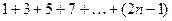, где n задается с клавиатуры.

1.3. Написать программу, позволяющую вычислить с помощью цикла:

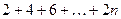, где n задается с клавиатуры.

1.4. Написать программу, позволяющую вычислить с помощью цикла:

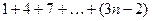, где n задается с клавиатуры.

1.5. Написать программу, позволяющую вычислить с помощью цикла:

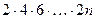, где n задается с клавиатуры.

1.6. Написать программу, позволяющую вычислить с помощью цикла:

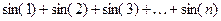, где n задается с клавиатуры.

1.7. Написать программу, позволяющую вычислить с помощью цикла:

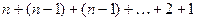, где n задается с клавиатуры.

1.8. Написать программу, позволяющую вычислить с помощью цикла сумму натуральных чисел отрезка [a, b]. (a и b задаются с клавиатуры).

1.9. Написать программу, позволяющую вычислить с помощью цикла сумму четных чисел отрезка [a, b]. (a и b задаются с клавиатуры).

1.10. Написать программу, позволяющую вычислить с помощью цикла сумму нечетных чисел отрезка [a, b]. (a и b задаются с клавиатуры).

1.11. Написать программу, позволяющую вычислить с помощью цикла:

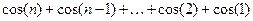, где n задается с клавиатуры.

1.12. Написать программу, позволяющую вычислить с помощью цикла:

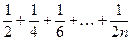, где n задается с клавиатуры.

1.13. Написать программу, позволяющую вычислить с помощью цикла:

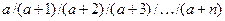, где a и n задаются с клавиатуры.

1.14. Написать программу, позволяющую вычислить с помощью цикла:

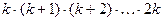, где k задается с клавиатуры.

1.15. Написать программу, позволяющую вычислить с помощью цикла:

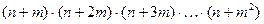, где n и m задаются с клавиатуры.

1.16. Написать программу, позволяющую вычислить с помощью цикла:

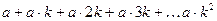, где a и k задаются с клавиатуры.

1.17. Написать программу, позволяющую вычислить с помощью цикла:

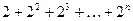, где n задается с клавиатуры.

1.18. Известно, какую сумму денег, на какой срок (в годах) и под какой годовой процент положил каждый из n бизнесменов в банк. Определить величину вклада каждого бизнесмена на конец срока.

1.19. Автомат, приклеивающий этикетки, работает со светлыми, зелеными и темными бутылками, в которые наливаются светлые и темные жидкости. Темные бутылки с темной жидкостью автомат разбивает. Сколько бутылок из 1997 штук разобьет автомат? Вид бутылки и жидкости задается случайным числом.

1.20. Пароход в понедельник проплывает случайное расстояние от А до В; во вторник — в два раза больше, чем в понедельник; в среду — в три раза меньше, чем во вторник; в четверг - на 40% больше, чем в среду; в пятницу - половину того, что он проплыл во вторник, среду и четверг вместе. В субботу и воскресенье пароход стоит. Определить полный путь парохода за n дней, если движение он начал в понедельник.

1.21. Татьяна Ларина, читая очередной французский роман, подсчитала сумму номеров прочитанных страниц. Написать программу, определяющую номер последней прочитанной страницы.

1.22. Вводятся N (3<=N<=1000) вещественных чисел. Напечатать все тройки соседних чисел, которые могут быть коэффициентами квадратного уравнения с вещественными корнями, вычислить сумму корней всех уравнений.

1.23. Жильцы всех квартир n-этажного дома из m подъездов с k квартирами на одной лестничной площадке решили прикрепить новые номера квартир. Кооператив, в который они обратились с просьбой изготовить необходимые им цифры, объявил, что цена каждой цифры равна ее значению. (Например, нули изготовляются бесплатно.) Жильцы решили оплатить стоимость заказа поровну. Написать программу для определения суммы взноса от каждой квартиры.

1.24. Каждый месяц клиент банка «Сохрани и помилуй» делает вклад 50,00 руб. на текущий счет. Банковский процент 6,5% от вклада рассчитывается помесячно (1/12 от 6,5% каждый месяц). Написать программу для расчета величины общего вклада, текущего счета и накопленной прибыли для каждого из 120 месяцев 10-летнего периода.

1.25. Продавщица Несчитайкина просит написать программу, которая по стоимости 1кг некоторого продукта выдавала бы таблицу стоимости 50, 100, 150, .., 1000, 2000, 3000, . . ., 10000 г этого продукта.

1.26. Вычислить для n слагаемых .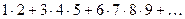

1.27. Некто взял ссуду в банке величиной А руб. под В% годовых. Ежегодно заемщик вносит платежи в счет ссуды в С руб. Написать программу, определяющую, через сколько лет будет погашена ссуда, и сумму денег, выплаченных заемщиком банку.

1.28. Первое любимое число Незнайки – 1, второе – 5. Каждое следующее число получается как сумма удвоенного предыдущего и предпредыдущего чисел. Так, третье любимое число – 11, а четвертое – 2 7. Вычислить сумму любимых чисел Незнайки среди первой тысячи.

1.29. Три года назад за покупку на базаре 1 кг картофеля, 1 л молока и одного десятка яиц уплачено А руб. С тех пор ежемесячно цена картошки увеличивалась на 3 0 %, цена молока — на 4 0 %, яиц в два раза. Написать программу ежемесячного изменения стоимости покупки, определяющую, через сколько месяцев цена , покупки увеличится более чем вдвое.

1.30. Богатый дядюшка подарил мне 1 доллар в мой первый день рождения. В каждый следующий день рождения он удваивал сумму подарка и прибавлял к ней столько долларов, сколько лет мне исполнилось. Написать программу, подсчитывающую общую сумму денег, подаренных к N-му дню рождения, и указывающую, к какому дню рождения сумма подарка превысит 100 долл.

1.31. Коммерсант ежемесячно увеличивает на z % и еще на 5 руб. цену туфель, первоначальная цена которых X руб. Написать программу, определяющую, через сколько месяцев цена туфель будет превышать Y руб. и какую прибыль за это время получит коммерсант, если инфляция составляет Q% в месяц.

1.32. Спортсмен, начав тренировки, в первый день пробежал 10 км. Каждый следующий день он увеличивал дистанцию на 12%. Написать программу, определяющую общую длину пробега за месяц и первый день с начала тренировок, после которого дистанция превысит 2 5 км.

1.33. Царевна-лягушка съедает ежедневно на 20% комаров больше, чем в предыдущий день, и еще два комара. Написать программу, определяющую, через сколько дней количество съеденных комаров превысит 100, если в первый день было съедено 12 комаров.

1.34. Написать программу, находящую наибольший общий делитель трех натуральных чисел a, b и с.

1.35. Подсчитать количество цифр в заданном целом числе n.

1.36. Найти сумму чисел, кратных n, на отрезке от а до b.

1.37. Меценат ежегодно вкладывает на развитие искусства столько денег, сколько он вложил в два предыдущих года, минус половина того, что он вложил тремя годами ранее. Написать программу, находящую сумму пожертвований мецената за n лет, если в первые три года он дал 1, 2, 2.5 млн руб. соответственно.

2. Задачи, решаемые методом перебора.

2.1. Найти все шестизначные числа с неубывающими слева направо цифрами, являющиеся полными квадратами.

2.2. Квадрат трехзначного числа оканчивается тремя цифрами, которые составляют взятое число. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.3. Квадрат трехзначного числа оканчивается тремя одинаковыми цифрами. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.4. Вместо каждой буквы в ребус АВВА=АА²+ВВ² подставить некоторую цифру, причем одинаковым буквам должны соответствовать одинаковые цифры, а различным буквам — различные цифры. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.5. Вместо каждой буквы в ребус КИО*ИО=ТОКИО подставить некоторую цифру, причем одинаковым буквам должны соответствовать одинаковые цифры, а различным буквам — различные цифры. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.6. Вместо каждой буквы в ребус СУК*СУК=БАРСУК подставить некоторую цифру, причем одинаковым буквам должны соответствовать одинаковые цифры, а различным буквам — различные цифры. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.7. Вместо каждой буквы в ребус (ЛИК)²=БУБЛИК подставить некоторую цифру, причем одинаковым буквам должны соответствовать одинаковые цифры, а различным буквам – различные цифры. Разработать схему алгоритма и написать программу для нахождения всех таких чисел.

2.8. Найти все трехзначные числа, которые делятся на каждую из цифр в их записи.

2.9. Найти все натуральные пятизначные числа вида 67m1n (m и n — цифры), которые делятся на 36.

2.10. Написать программу, определяющую сумму всех возможных трехзначных чисел, содержащих только нечетные цифры. Определить также, сколько четных цифр в найденной сумме.

2.11. Среди дробей вида m/n, где m и n — целые двузначные числа, найти дробь, наиболее близкую к числу .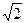

2.12. Найти все трехзначные числа, каждое из которых в 19 раз больше суммы своих цифр.

2.13. Найти все натуральные трехзначные числа, каждое из которых обладает следующими свойствами:

- первая цифра в три раза меньше последней его цифры;

- сумма самого числа с числом, получающимся из него перестановкой второй и третьей цифр, делится на 8 без остатка.

2.14. Сколько имеется двузначных чисел, сумма квадратов цифр которых делится на 13?

2.15. Найти двузначное число, равное сумме цифры его десятков и квадрата цифры единиц.

2.16. Если к сумме цифр двузначного числа прибавить квадрат этой суммы, то снова получится двузначное число. Найти все такие числа.

2.17. Найти четырехзначное число, которое при делении на 133 дает в остатке 125, а при делении на 134 дает в остатке 111.

2.18. Дополнить число 523*** цифрами справа так, чтобы
полученное шестизначное число делилось на 7, 8 и 9 одновременно.

2.19. Найти наименьшее натуральное число Х>1, которое при
делении на 2, 3, 4, 5 и 6 дает в каждом случае остаток 1.

2.20. Дополнить число ***999 цифрами слева так, чтобы полученное шестизначное число делилось на 13, 17 и 19.

2.21. Найти трехзначное число, квадрат которого оканчивается тремя одинаковыми цифрами, отличными от нуля.

2.22. Дополнить число 42*4* цифрами так, чтобы полученное пятизначное число делилось на 72.

2.23. Найти четырехзначное число, у которого две первые и две последние цифры одинаковы, являющееся квадратом. Квадрат — это число, квадратный корень из которого является целым числом.

2.24. Найти все пятизначные числа вида 2*57*, которые делятся на 15.

2.25. Найти все трехзначные числа, равные сумме кубов своих цифр.

2.26. В трехзначном числе зачеркнули первую цифру слева; когда полученное двузначное число умножили на 7, получилось исходное трехзначное число. Найти его.

2.27. В трехзначном числе, все цифры которого нечетны, зачеркнули среднюю цифру. Оказалось, что полученное двузначное число является делителем исходного числа. Найти все такие трехзначные числа.

2.28. Сумма цифр трехзначного числа кратна 7. Само число также делится на 7. Найти все такие числа.

2.29. Четырехзначное число, а также число, записанное теми же цифрами в обратном порядке, являются квадратами. Найти эти числа.

2.30. Найти все двузначные числа, сумма цифр которых не меняется при умножении на 2, 3, 4, 5, 6, 7, 8, 9.

2.31. Сколько слагаемых суммы 1+2+3+... надо взять, чтобы получилось трехзначное число, состоящее из одинаковых цифр?

2.32. Сколько имеется целых чисел от 1 до 2005, которые не делятся на 6, 10,15?

2.33. Найти наименьшее натуральное число М, такое, что сумма квадратов 11 последовательных натуральных чисел, начиная с М, является квадратом.

2.34. Найти четырехзначное число, в четыре раза меньшее числа, записанного теми же цифрами в обратном порядке.

2.35. Трехзначное число начинается с цифры 7. Из него получили другое трехзначное число, переставив эту цифру в конец числа. Полученное число оказалось на 117 меньше предыдущего. Какое число рассматривалось?

2.36. Найти все пары натуральных чисел, сумма квадратов которых равна 16000.

2.37. Найти сумму всех трехзначных чисел, в записи которых все цифры нечетные.

2.38. Выписать в порядке возрастания все четырехзначные натуральные числа, сумма цифр которых делится на 5.

2.39. Найти последнюю цифру суммы всех трехзначных чисел, десятичная запись которых не содержит цифру 3.

2.40. Найти последнюю цифру суммы всех пятизначных натуральных чисел, десятичная запись которых не содержит цифры 7.

2.41. Найти все пятизначные числа вида 6*93*, которые делятся на 15.

2.42. Найти все пятизначные числа вида 517**, которые делятся на 18.

2.43. Найти все пятизначные числа вида 74*3*, которые делятся на 45.

2.44. Найти все пятизначные числа, равные кубу числа, образованного двумя последними их цифрами.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Тульский государственный университет»

Политехнический институт

Кафедра «Сварка, литье и технология конструкционных материалов»