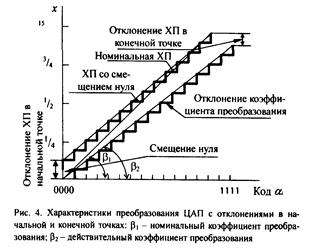
Нелинейности

Нелинейность в данной точке ХП - это отклонение точки реальной ХП от прямой, проведенной определенным образом. Нелинейность может быть определена двумя спо­собами: 1) нелинейность находится относительно прямой (рис. 4), проведенной через начальную и конечную точки ХП; 2) нелинейность находится относительно прямой, проведенной таким образом, чтобы минимизировать зна­чение нелинейности, например, относительно прямой, среднее квадратическое отклонение всех точек которой минимально. Уравнение такой прямой V = Ax + В, где В -коэффициент, равный смещению нуля; А - коэффициент, определяющий крутизну характеристики. Значения коэф­фициентов^ и В находятся по формулам:

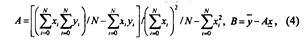
Для ЦАП нелинейность, как правило, определяется нелинейностью в точке ХП, где она по абсолютной вели­чине максимальна. Нелинейность выражается в долях ЕМП или в процентах от значения аналоговой величины в конечной точке ХП:

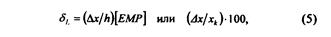
Дифференциальная нелинейность - это отклонение действительных ступеней квантования от их среднего значения. Дифференциальная нелинейность ('-и ступени квантования

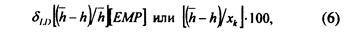
где h, h - действительное и среднее значения ступени квантования.

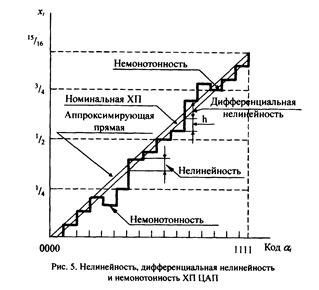
Для ЦАП указывается значение дифференциальной нелинейности той точки характеристики, где это значение по абсолютной величине максимально. Дифференциальная нелинейность имеет прямую связь с монотонностью ХП.

Под монотонностью понимается неизменность знака при­ращения выходной величины при последовательном изме­нении значения входного кода. Если дифференциальная нелинейность в некоторой точке по абсолютной величине превышает 1 ЕМР, то это значит, что приращение выходной аналоговой величины в этой точке может иметь противо­положное предыдущей точке направление или быть боль­ше двойной номинальной ступени квантования (рис. 5).

Нелинейность и дифференциальная нелинейность в некоторых случаях определенным образом связаны, однако эта связь не является однозначной. Если изменение выход­ной аналоговой величины при включении отдельных раз­рядов не зависит от состояния других разрядов (включен или выключен), то дифференциальная нелинейность не может превышать удвоенного значения нелинейности