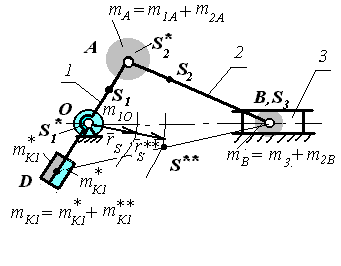
Частичное уравновешивание для случая, когда центр масс движется по дуге, хорда которой перпендикулярна оси направляющей ползуна
Каждое звено заменяется двумя сосредоточенными массами, с использованием систему уравнений (10.4) и (10.5):
Массы, размещенные в точках А и В, объединяются:
mА = m1А + m2А, mВ = m2В + m3.
Данный механизм уравновешивается корректирующей массой mК1:
mК1 = 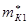 +
+ 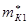
|
Корректирующая масса 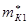 уравновешивает массу mА:
уравновешивает массу mА: 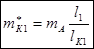 .
.
Корректирующая масса 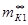 уравновешивает массу mВ. Ее величина находится из условия, что центр масс
уравновешивает массу mВ. Ее величина находится из условия, что центр масс 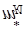 и mА расположен в т.О. Центр масс
и mА расположен в т.О. Центр масс 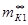 и mВ лежит на прямой BD и делит ее в отношении x/y , т.е
и mВ лежит на прямой BD и делит ее в отношении x/y , т.е 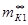 ×x = mВ×y . Через отрезок OS** проведем прямую параллельную АВ и тогда из подобия треугольников найдем:
×x = mВ×y . Через отрезок OS** проведем прямую параллельную АВ и тогда из подобия треугольников найдем:
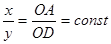 ;
; 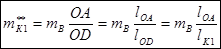 .
.
Суммарная корректирующая масса 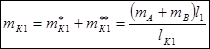 .
.
Радиус-вектор центра масс находится из соотношений:
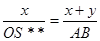 ;
; 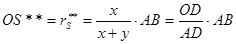 ;
;
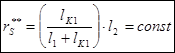 .
.
Дата добавления: 2015-03-14; просмотров: 790;
