КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ ІМ.В.ГЕТЬМАНА

ОБРАЗЦЫ из учебника!!!

Пример 4.4.1. Исследовать функцию 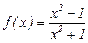и построить её график.

Решение.

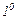.Область определения функции: 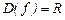, т. е. вся числовая ось.

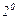.Исследуем функцию на чётность-нечётность, периодичность.

.

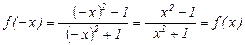Таким образом, функция чётная, следовательно, график функции симметричен относительно оси . Не периодическая.

Найдём вертикальные асимптоты. Исследуем поведение функции на бесконечности, найдём наклонные асимптоты.

а) Вертикальных асимптот нет, так как нет точек разрыва.

б) Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты .

Так как функция четная, то исследуем поведение функции одновременно при .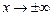

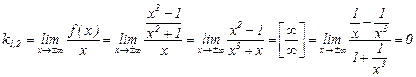
Соответственно,

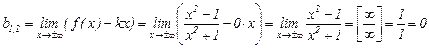
Следовательно, мы имеем 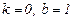, т. е. при 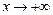так и при 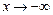функция имеет одну и ту же горизонтальную асимптоту .

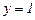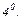Исследуем функцию по нулевой производной, т. е. найдём интервалы знакопостоянства.

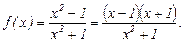
Исследуем функцию по первой производной, т. е. найдём точки экстремума функции и интервалы возрастания и убывания.

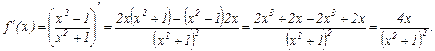
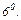Исследуем функцию по второй производной, т. е. найдём точки перегиба графика функции и интервалы выпуклости и вогнутости.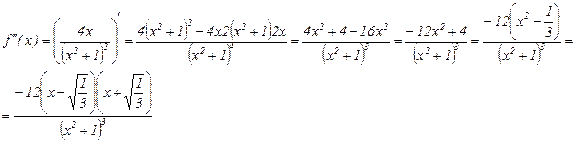

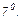Таблица. Для удобства сведём накопленную информацию в таблицу:

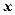
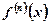
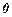
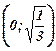
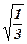
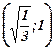
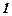
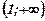
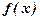
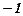
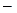
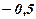
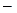
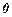
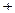
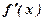
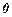
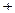
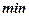
	возрастает
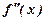
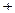
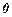
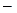
вогнута		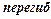выпукла

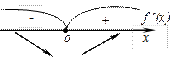
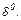График. Используя таблицу, строим график функции (Рис. 4.4.1).

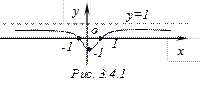
Пример 4.4.2.Исследовать функцию 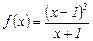и построить её график.

Решение.

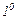Область определения функции: .

 

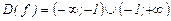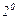. Исследуем функцию на чётность-нечётность, периодичность. 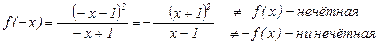. Не периодическая.

 

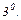Найдём вертикальные асимптоты. Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты.

а) Вертикальные асимптоты ищутся среди точек разрыва, т. е. в нашем случае рассмотрим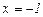

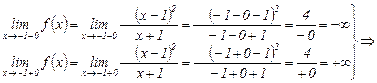
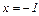–вертикальная асимптота.

б) Исследуем поведение функции на бесконечности, найдём наклонные (горизонтальные) асимптоты . ,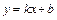

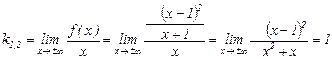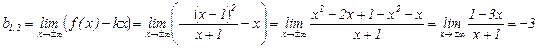
Следовательно, при 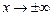мы имеем наклонную асимптоту .

 

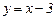Исследование по нулевой производной, т. е. найдём интервалы знакопостоянства.

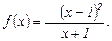
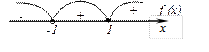
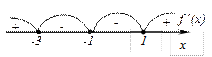
Исследование по первой производной, т. е. найдём точки экстремума функции и интервалы возрастания и убывания.

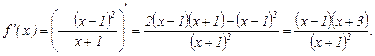
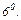Исследование по второй производной, т. е. найдём точки перегиба графика функции и интервалы выпуклости и вогнутости.

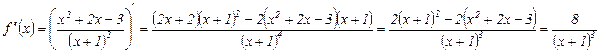
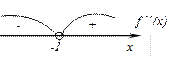
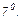Таблица. Для удобства сведём накопленную информацию в таблицу:

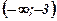
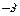
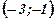
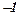
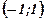
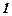
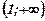
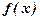
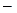
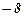
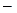
				Не существует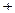
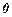
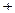
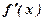
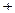
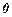
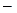
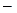
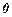
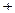
возрастает		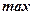убывает	убывает		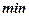возрастает
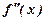
выпукла	вогнута

 

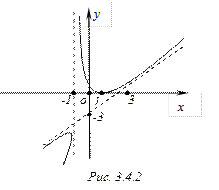
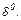График. Используя таблицу, строим график функции (Рис.4.4.2).

Рис. 4.4.2

 

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ ІМ.В.ГЕТЬМАНА