Сооружений

Горизонтальные смещения сооружений или их отдельных элементов измеряют различными способами, основными из которых являются: линейно-угловой, створный и стереофотограмметрический. Применяют также прямые и обратные отвесы.

Линейно-угловые построения применяют в случае, когда величины смещений необходимо знать по двум координатам. Эти построения могут развиваться в виде специальных сетей триангуляции и трилатерации, комбинированных сетей, угловых и линейных засечек, ходов полигонометрии, сетей из вытянутых треугольников с измеренными сторонами и высотами.

Применение того или иного вида построения зависит от характера сооружения и его геометрической формы, требуемой точности и условий измерений, организационных и других факторов. Так, например, угловую и линейную засечки применяют для определения смещений недоступных точек сооружения, а триангуляцию, полигонометрию, сети из вытянутых треугольников с измеренными сторонами и высотами — для протяженных сооружений криволинейной формы. Во многих случаях применяют комбинированные схемы, когда, например, триангуляция или трилатерация используются для определения устойчивости исходных пунктов, с которых способами засечек или полигонометрии определяются смещения точек на сооружении.

Применительно к измерениям деформаций каждый из видов линейно-угловых построений обладает своими особенностями. однако для всех видов характерным является постоянство схемы измерений и необходимость получения в конечном итоге не самих координат деформационных точек, а их изменений во времени, т. е. разностей координат в двух циклах.

для специальной триангуляции характерна высокая точность измерения углов (0,5’’ — 2,0”) при коротких сторонах, большое количество связей, обеспечивающих минимальную величину обратного веса определения функции координат точек сети.

Полигонометрия применяется в основном в виде одиночных ходов, опирающихся на исходные пункты. Часто из-за невозможности азимутальной привязки используют лишь привязку координатную.

Уравнивание линейно-угловых построений производят строгими способами. Координаты пунктов вычисляют в условной системе.

Створные наблюдения широко применяют для исследования деформаций сооружений прямолинейной формы, когда смещения достаточно знать по одному направлению. При этом координатную систему выбирают так, чтобы с направлением смещений совпадала ось ординат, а с направлением створа — ось абсцисс.

Величины смещений находятся по разности значений ординат (нестворностей), измеренных в двух циклах.

Нестворность определяют различными методами, из которых наиболее распространены методы подвижной марки и малых углов. для задания створной линии применяют струнные и оптические способы, а также способы, основанные на принципах физической оптики.

Струнный способ предусматривает использование натянутой стальной струны различного диаметра, оптический — зрительных труб большого увеличения (теодолиты, нивелиры, автоколлимационные системы, специальные алиниометры).

В методе подвижной марки величина нестворности определяется непосредственно. для этого в точку А (рис. 19.5, а) устанавливается оптический прибор, коллимационная плоскость которого ориентируется по марке в точке В и задает створную линию. Подвижная марка, установленная в точке С, вводится в створ. Положение подвижной марки, когда мишень ее находится в створе, фиксируется по отсчетному устройству марки. Если известен отсчет, когда ось мишени совпадает с точкой С, то нестворность q_с может быть вычислена как разность отсчетов при положении марки в точке С и в створе АВ. При возможности поворота марки на 180° нестворность может быть получена как полуразность отсчетов для двух положений марки при введении ее в створ.

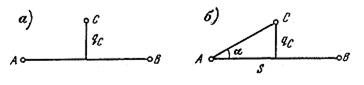
Рис. 19.5. Определение величины нестворности методами: подвижной марки а), малых углов б).

В методе малых углов нестворность q определяется путем измерения малого угла α (рис. 19.5, б) между линией створа и направлением на точку С и расстояния S.

Для створов значительной протяженности с большим числом определяемых точек на створе в зависимости от условий измерений применяют различные схемы (программы) наблюдений. Простейшая из них — схема общего створа (рис. 19.6, а), когда нестворности всех точек определяются относительно общего створа между концевыми (опорными) точками створа.

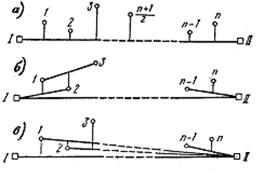
Рис. 19.6. Схемы створных измерений.

В схемах частных (пересекающихся) (рис. 19.6, б) и последовательных (19.6, в) створов нестворности измеряются между определяемыми точками относительно этих створов.

Так, схема последовательных створов предусматривает определение нестворностей Δ₁ точки 1 от створа I – II, Δ₂ точки 2 от створа 1 – II, Δ₃ точки 3 от створа 2 – II и т.д.

В обеих схемах нестворности q относительно общего створа могут быть получены лишь путем соответствующих вычислений, зная расстояния S между всеми точками.