Program MetodHord;
Const Eps=0.0001; h=0.1;
Var alfa,beta,X,dX, x1,x2,y1,y2:Real; k:integer;
Function F(xf:Real):Real;
Begin
F:=Sqr(xf)*xf-1.2*xf+1;
End;
Function d2F(x1,x2:Real):Real;
Function ddF(xf:Real):Real;
Begin
ddF:=6*xf
End;
Var S:Real;
Begin
S:=0;
While x1<=x2 do
Begin
S:=S+ddF(x1); x1:=x1+h/2;
End;
d2F:=S;
End;
Function XA(a,xn:Real):Real;
Begin
XA:=Xn-(F(Xn)/( F(a)-F(Xn) ))*(a-Xn)
End;
Function XB(b,Xn:Real):Real;
Begin
XB:=Xn-(F(Xn)/(F(b)-F(Xn)))*(b-Xn)
End;
Procedure MH(a,b:Real; Var Xn,dX1:Real;var k:integer);
Var y,Xn1:Real;
Begin
If F(b)*d2F(a,b)>0
Then
Begin
Xn:=a; y:=F(Xn);
Repeat
Xn1:=Xb(b,xn); y:=F(Xn1); Xn:=Xn1;inc(k);
Until Abs(Xn-Xn1)<=Eps;
dX1:=Abs(Xn-Xn1);
End;
If F(a)*d2F(a,b)>0
Then
Begin
Xn:=b; y:=F(Xn);
Repeat
Xn1:=Xa(a,xn); y:=F(Xn1); Xn:=Xn1; inc(k);
Until Abs(Xn-Xn1)<=Eps ;
dX1:=Abs(Xn-Xn1);
End
End;
Begin {отделение корней}
Write(‘Введите отрезок : '); ReadLn(Alfa,Beta);
x1:=alfa;
x2:=x1+h;
y1:=F(x1);
While x2<=beta do
Begin
y2:=F(x2);
If y1*y2<=0
Then
Begin
WriteLn(‘Корень определен на промежутке ( ',x1:4:1,' ; ',x2:4:1,' )');
MH(x1,x2,X,dX,k);
WriteLn('X = ',X:10:8,' +- ',dX:10:8); WriteLn(k);
End;
If y1*y2=0
Then
Begin
x2:=x2+h;
y2:=F(x2);
End;
x1:=x2;
x2:=x1+h;
y1:=y2;
End;
If X=0 Then WriteLn(‘На этом промежутке нет корней.');
End.
Тестовый пример:
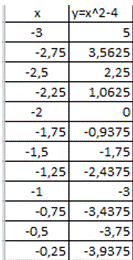
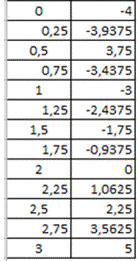
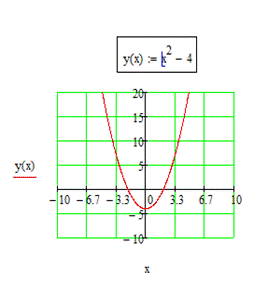
Найти корень нелинейного уравнения F(x) ≡ x2-4 = 0
x1=-2 & x2=2.
Протокол:
|
Проверка и вывод:
Решение задачи: 
|
Проверка и вывод:
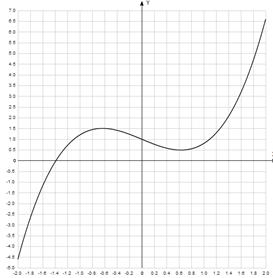
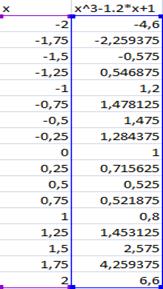
График функции пересекает ось абсциссы на [-2;-1]. Уточним его методом хорд. Для этого определим знаки функции 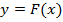 и второй её производной
и второй её производной 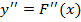 на этом отрезке [-2;-1].
на этом отрезке [-2;-1].
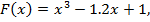
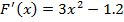
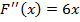
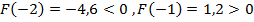 ;
; 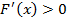 ,
, 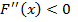 для любого x из [-2;-1].
для любого x из [-2;-1].
Поскольку 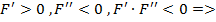 , то применяем формулу
, то применяем формулу
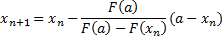
где 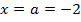 – неподвижная точка,
– неподвижная точка, 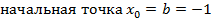 . Получим следующую таблицу.
. Получим следующую таблицу.
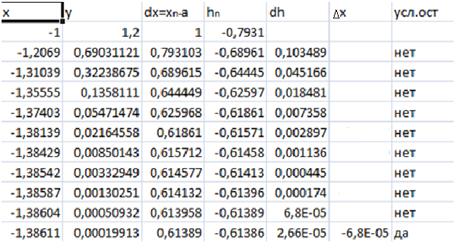

Где 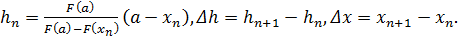
Приблизительная схема применения метода:
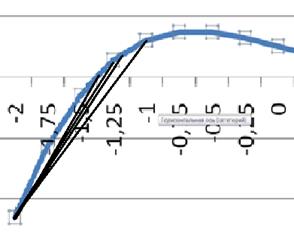
Оценим погрешность приближения. Так как 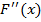 не меняет свой знак на данном отрезке, то
не меняет свой знак на данном отрезке, то 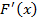 достигает своего наибольшего и наименьшего значения на концах отрезка [-2;-1], поэтому
достигает своего наибольшего и наименьшего значения на концах отрезка [-2;-1], поэтому 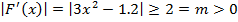 для любого
для любого 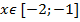 .
.
Тогда используя оценку погрешности
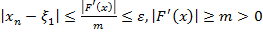 для любого
для любого 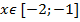 .
.
Получим 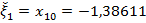 ,
, 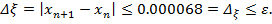
Следовательно, приближенное значение корня равно
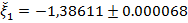 .
.
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
Имеем 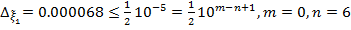 . Округлим
. Округлим 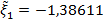 до
до 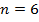 . Получим
. Получим 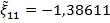 ,
, 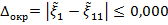 ,
, 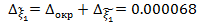 .
.
Найдем число верных знаков для 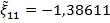 . Имеем
. Имеем 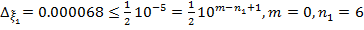 . Так как
. Так как 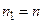 , то получим приближенное значение корня с числом верных знаков
, то получим приближенное значение корня с числом верных знаков 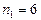 .
.
Ответ: 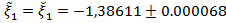 .
.
2. Метод касательных (Ньютона).
Тема: Решение нелинейного уравнения методом касательных (Ньютона).
Постановка задачи: Найти корень нелинейного уравнения 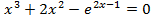 методом касательных с точностью
методом касательных с точностью 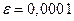 .
.
Краткая теория: Дано нелинейное уравнение F(x) =0, где функция у = F(x) определена и непрерывно-дифференцируема для всех 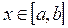 , причем функция меняет знак на концах этого отрезка т.е. F(a) · F(b) < 0.
, причем функция меняет знак на концах этого отрезка т.е. F(a) · F(b) < 0.
Приближенное решение ξ ;и погрешность приближения Δξ;находятся по следующей схеме:
если F(b) · F"(x) > 0 на [a,b], то 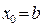 ;
;
если F(a) · F"(x) > 0 на [a,b], то 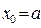 ;
;
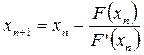 ,
, 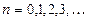 .
.
Приближенное решение ξ, и погрешность приближения Δξ:
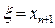 ,
, 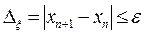 .
.
Блок-схемы:
Отделение корнейМетод касательных
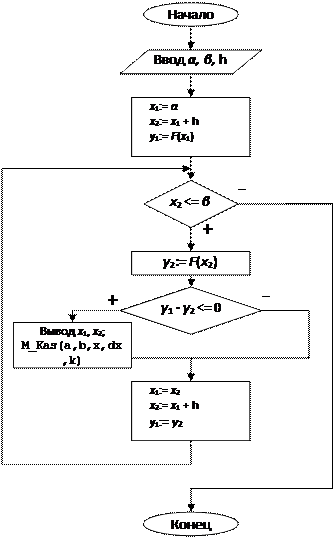
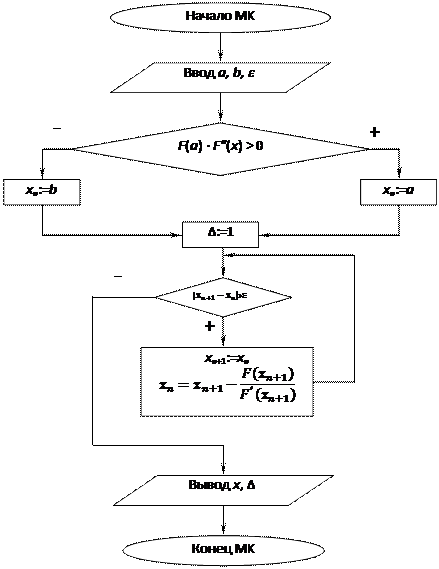 |
Текст программы:
Program Metod_Kasateln;
Const Eps=0.0001; H=0.25;
Var alfa,beta,X,dX, x1,x2,y1,y2:Real; k:integer;
Function F(xf:Real):Real;
Begin
F:=Cos(xf-1)-Sqr(xf)/3
End;
Function dF(Xf:Real):Real;
Begin
dF:=-Sin(xf-1)-2/3*xf
End;
Function d2F(x1,x2:Real):Real;
Function ddF(xf:Real):Real;
Begin
ddF:=-Cos(xf-1)-2/3
End;
VarS:Real;
Begin
S:=0;
While x1<=x2 do
Begin
S:=S+ddF(x1);
x1:=x1+H/2;
End;
d2F:=S;
End;
Procedure M_Kas(a,b:Real; Var Xn,dX1:Real;var k:integer);
Var Xn1:Real;
Begin
If F(a)*d2F(a,b)>0
Then Xn:=a
Else Xn:=b;
dX1:=1;
While Abs(dx1)>EPS do
Begin
Xn1:=Xn;
Xn:=Xn1-F(Xn1)/dF(Xn1);
dX1:=Xn1-Xn; inc(k);
End;
End;
Begin {Отделение корней}
Write('Введите промежуток : '); ReadLn(Alfa,Beta);
x1:=alfa;
x2:=x1+H;
y1:=F(x1);
While x2<=beta do
Begin
y2:=F(x2);
If y1*y2<=0
Then
Begin
WriteLn('Корень определен на промежутке ( ',x1:0:2,' ; ',x2:0:2,' )');
M_Kas(x1,x2,X,dX,k);
WriteLn('X = ',X:10:8,' +- ',dX:10:8); WriteLn(‘Количество итерации=’,k);
End;
If y1*y2=0
Then
Begin
x2:=x2+H; y2:=F(x2);
End;
x1:=x2; x2:=x1+H; y1:=y2;
End;
If X=0 Then WriteLn('На этом промежутке корней НЕ СУЩЕСТВУЕТ.');
End.
Тестовый пример:
Найти корень нелинейного уравнения 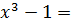 0
0
x1=1.00.
Второй и третий корень мнимый.
|
Протокол:
Проверка и вывод
Проверка и вывод:
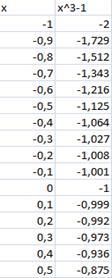
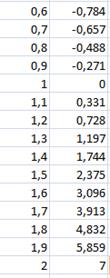
Решение задачи: 
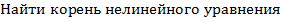
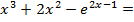 0.
0.
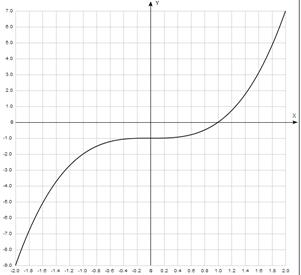
График уравнения:
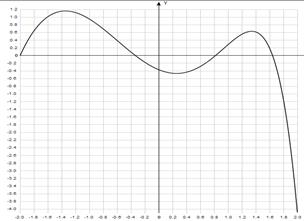
Протокол:
|
Отделим корни уравнения графически (и программно). Для этого построим график функции 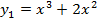 и
и 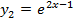 и найдем абсциссы точек пересечения графиков этих функций:
и найдем абсциссы точек пересечения графиков этих функций: 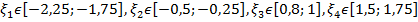 .
.
Проверка и вывод:
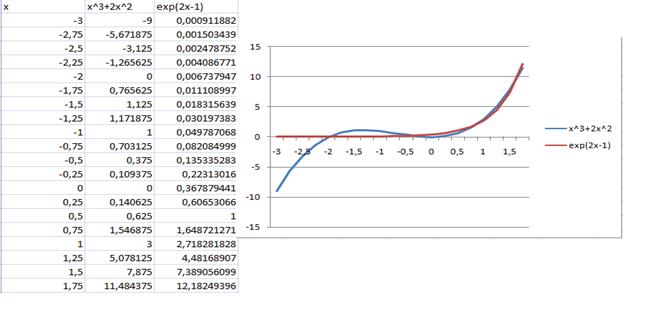
В качестве примера рассмотрим первый и второй корень.
Уточним корни методом касательных:
1) 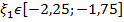 . Для этого определим знаки функции
. Для этого определим знаки функции 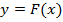 и второй её производной
и второй её производной 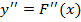 на этом отрезке [-2,25;-1,75].
на этом отрезке [-2,25;-1,75].
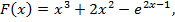
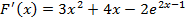
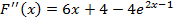
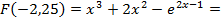 -9,000911882<0 ,
-9,000911882<0 ,
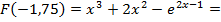 0,754516003>0
0,754516003>0
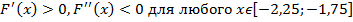 . Тогда
. Тогда 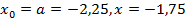
Применяем формулу 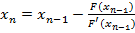 .
.
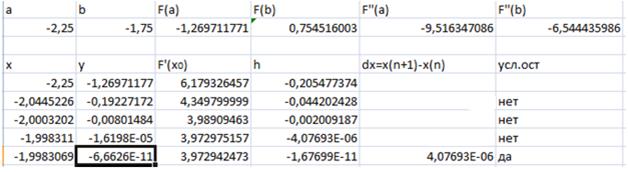
Оценим погрешность приближения. Так как 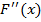 не меняет свой знак на данном отрезке, то
не меняет свой знак на данном отрезке, то 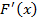 достигает своего наибольшего и наименьшего значения на концах отрезка [-2,25;-1,75], поэтому
достигает своего наибольшего и наименьшего значения на концах отрезка [-2,25;-1,75], поэтому 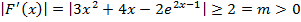 для любого
для любого 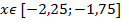 .
.
Тогда используя оценку погрешности
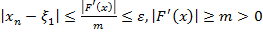 для любого
для любого 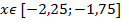 .
.
Получим 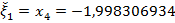 ,
, 
Следовательно, приближенное значение первого корня равно
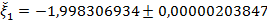 .
.
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
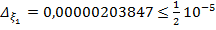
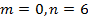 . Округлим
. Округлим 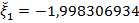 до
до 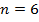 .
.
Получим 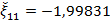 , с погрешностью округления
, с погрешностью округления 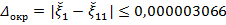 .
. 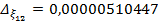 .
.
Найдем число верных знаков для 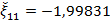 .
. 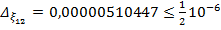
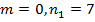 .
. 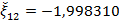 .
. 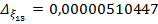 .
. 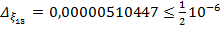
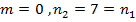 . Следовательно
. Следовательно 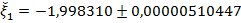 .
.
Ответ: 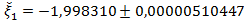
2) 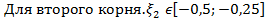 . Для этого определим знаки функции
. Для этого определим знаки функции 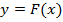 и второй её производной
и второй её производной 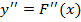 на этом отрезке
на этом отрезке 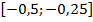 .
.
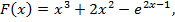
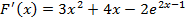
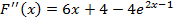
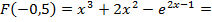 0,239664717>0
0,239664717>0
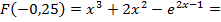 -0,11375516<0
-0,11375516<0
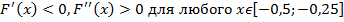 . Тогда
. Тогда 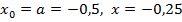
Применяем формулу 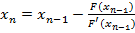 .
.
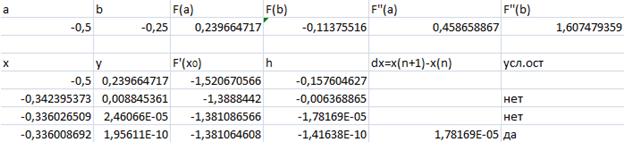
Оценим погрешность приближения. Так как 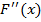 не меняет свой знак на данном отрезке, то
не меняет свой знак на данном отрезке, то 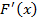 достигает своего наибольшего и наименьшего значения на концах отрезка
достигает своего наибольшего и наименьшего значения на концах отрезка 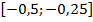 , поэтому
, поэтому 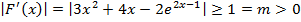 для любого
для любого 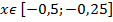 .
.
Тогда используя оценку погрешности
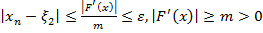 для любого
для любого 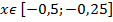 .
.
Получим 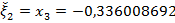 ,
, 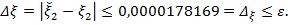
Следовательно, приближенное значение второго корня равно
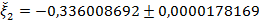 .
.
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
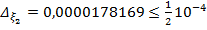
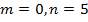 . Округлим
. Округлим 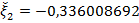 до
до 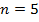 .
.
Получим 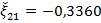 , с погрешностью округления
, с погрешностью округления 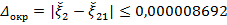 .
. 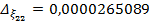 .
.
Найдем число верных знаков для 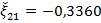 .
. 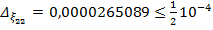
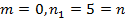 . Следовательно
. Следовательно 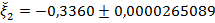 .
.
Ответ: 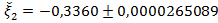 .
.
3. Комбинированный метод хорд и касательных.
Тема: Решение нелинейного уравнения методом хорд и касательных.
Постановка задачи: Найти корень нелинейного уравнения 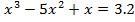 методом хорд с точностью
методом хорд с точностью 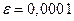 .
.
Краткая теория:
Дано нелинейное уравнение, где функция 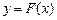 определена и непрерывно-дифференцируема для всех
определена и непрерывно-дифференцируема для всех 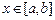 , причем функция меняет знак на концах этого отрезка, т.е.
, причем функция меняет знак на концах этого отрезка, т.е. 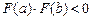 .
.
Найти приближенное решение данного уравнения 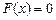 с точностью
с точностью 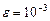 .
.
Приближенное решение 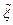 и погрешность приближения
и погрешность приближения 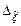 находятся по следующей схеме:
находятся по следующей схеме:
если 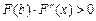 на
на 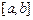 , то
, то 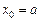 ,
, 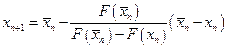
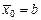 ,
, 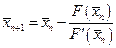 ,
, 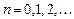 ;
;
если 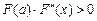 на
на 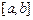 , то
, то 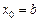 ,
, 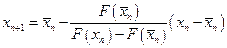 ,
,
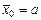 ,
, 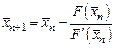 ,
, 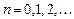 .
.
Приближенное решение 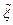 и погрешность приближения
и погрешность приближения 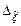 :
:
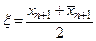 ,
, 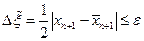 .
.
Блок-схемы:
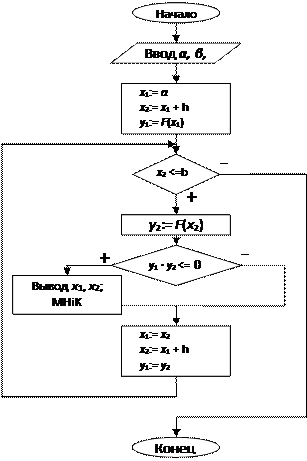
 Отделение корнейКомбинированный метод хорд и касательных
Отделение корнейКомбинированный метод хорд и касательных
Текст программы:
Program Metod_KiH;
Const Eps=0.0001;h=0.25;
Var alfa,beta,X,dX, x1,x2,y1,y2:Real;
Function F(xf:Real):Real;
Begin
F:=xf*xf*xf-5*xf*xf+xf-3.2;
End;
Function dF(xf:Real):Real;
Begin
dF:=3*xf*xf-10*xf+1;
End;
Function ddF(xf:Real):Real;
Begin
ddF:=6*xf-10;
End;
Procedure MC(a,b:Real;Var x1,dx1:Real);
Var xn1, xn2,xp1,xp2:Real;
Begin
If F(a)*ddF(a)>0
Then
Begin
xn1:=b; xn2:=a;
End
Else
Begin
xn1:=a; xn2:=b;
End;
dx1:=1;
While Abs(dx1)>EPS do
Begin
xp1:=xn1; xp2:=xn2; xn1:=xp1-(F(xp1)/(F(xp2)-F(xp1)))*(xp2-xp1);
xn2:=xn2-F(xp2)/dF(xp2); dx1:=Abs((xn2-xn1)/2);
End;
x1:=(xn1+xn2)/2;
End;
Begin {Отделение корней}
Write('Введите промежуток : '); ReadLn(Alfa,Beta);
x1:=alfa; x2:=x1+h;
y1:=F(x1);
While x2<=beta do
Begin
y2:=F(x2);
If y1*y2<=0
Then
Begin
WriteLn('Корень определен на промежутке ( ',x1:0:2,' ; ',x2:0:2,' )');
MC(x1,x2,X,dX);
WriteLn('X = ',X:10:8,' +- ',dX:10:8);
End;
If y1*y2=0
Then
Begin
x2:=x2+h; y2:=F(x2);
End;
x1:=x2; x2:=x1+h; y1:=y2;
End;
If X=0 Then WriteLn('На этом промежутке корней НЕ СУЩЕСТВУЕТ.');
End.
Тестовый пример:
Найти корень нелинейного уравнения 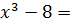 0
0
x1=2.00 & x2=-1+i 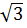 & x3=-1-i
& x3=-1-i  .
.
Протокол:
|
Проверка и вывод
Проверка и вывод:
Решение задачи: 
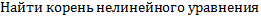
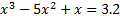
Протокол:
|
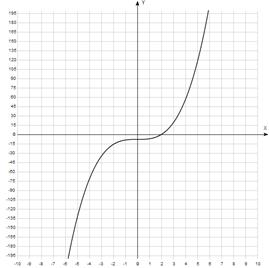
График уравнения:
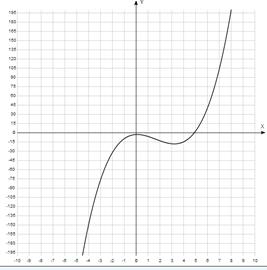
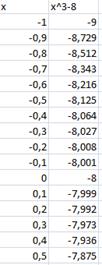
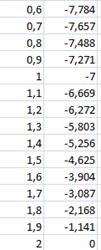
Отделим корни уравнения графически. Для этого построим график функции 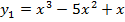 и
и 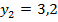 и найдем абсциссы точек пересечения графиков этих функций:
и найдем абсциссы точек пересечения графиков этих функций: 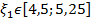 .
.
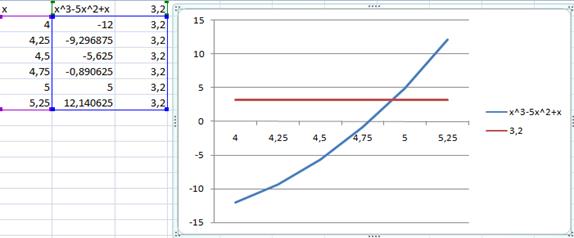
Уточним корни методом касательных:
1) 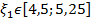 . Для этого определим знаки функции
. Для этого определим знаки функции 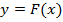 и второй её производной
и второй её производной 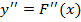 на этом отрезке
на этом отрезке 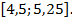
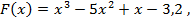
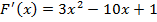
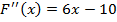
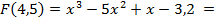 -8,825<0 ,
-8,825<0 , 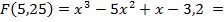 8,940625>0
8,940625>0
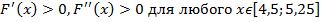 . Тогда
. Тогда 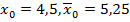
Применяем формулы 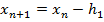 ,
, 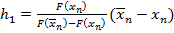 ,
, 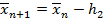 ,
, 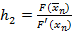 .
.
Процесс продолжаем до выполнения условия | 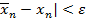 , тогда за приближенное значение корня можно взять значение
, тогда за приближенное значение корня можно взять значение
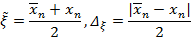

Оценим погрешность приближения. Так как 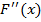 не меняет свой знак на данном отрезке, то
не меняет свой знак на данном отрезке, то 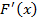 достигает своего наибольшего и наименьшего значения на концах отрезка
достигает своего наибольшего и наименьшего значения на концах отрезка 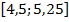 , поэтому
, поэтому 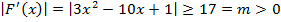 для любого
для любого  .
.
Тогда используя оценку погрешности
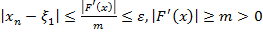 для любого
для любого  .
.
Получим 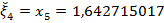 ,
, 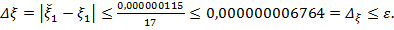
Следовательно, приближенное значение корня равно
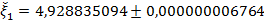 .
.
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
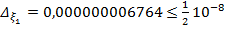
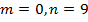 . Округлим
. Округлим 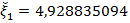 до
до 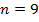 .
.
Получим 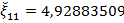 , с погрешностью округления
, с погрешностью округления 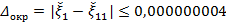 .
. 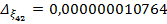 .
.
Найдем число верных знаков для 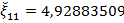 .
. 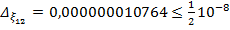
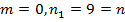 .
.
Следовательно, 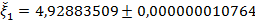 .
.
Ответ: 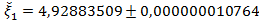 .
.
Дата добавления: 2014-11-30; просмотров: 931;
