Круглый стол

Вслед за уроком, в котором я рассказывал вам, какпостроить линию пересечения цилиндра с наклонной плоскостью, пришло время опубликовать статью о построении линии пересечения конуса и наклонной плоскости. Умение построить линию пересечения конуса с плоскостью может пригодится вам при построении натурального вида фигуры сечения или же просто, при решении простой задачи о сечении конуса. В любом случае, в курсе инженерной графики вы как минимум раз с этим столкнетесь. Так пусть же это столкновение пройдет для вас менее болезненно. В противном случае, пишите, звоните, будем договариваться :)

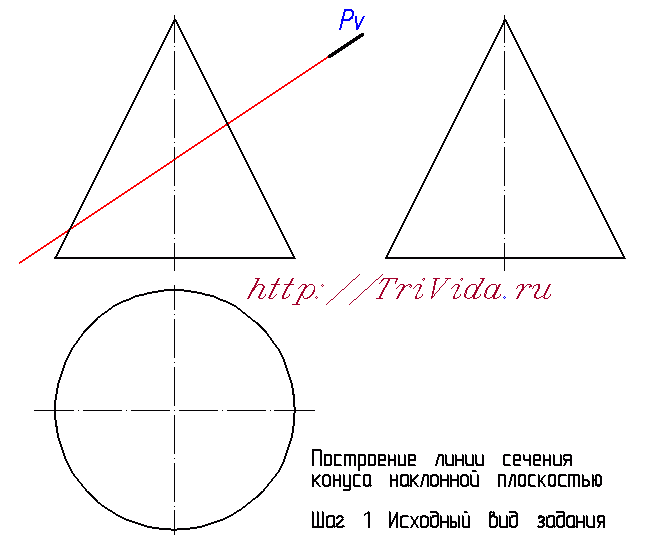
Итак, приступим. На рисунке ниже вы видите среднестатистический чертеж в том виде, в котором вы получаете задание на сечение конуса плоскостью. С той лишь поправкой, что обычно на нем не изображен третий вид. Его я начертил заранее, подготовив для будущих построений.

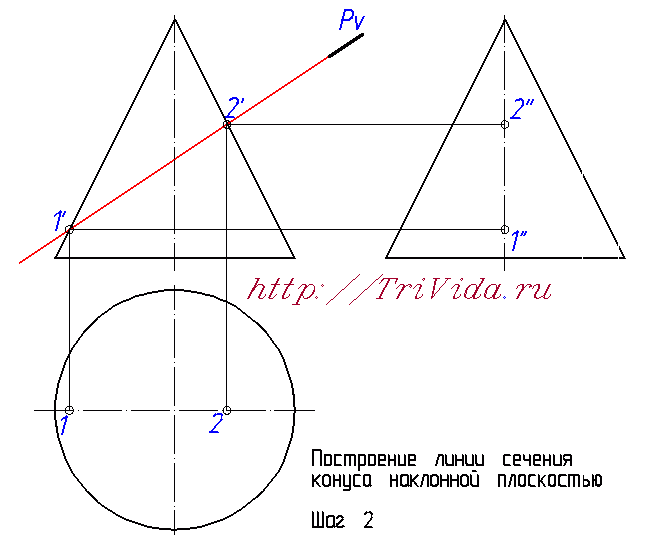
Первым делом обозначим точки, в которых плоскость пересекает образующие конуса на фронтальной проекции. Снесем их на горизонтальную проекцию до пересечения с осью, а так же на профильную проекцию - так же до пересечения с осью. Отмечу, что точка 2'' будет невидимой (на рисунке это явно не указано).

Пришло время сказать кое-какие важные вещи, касаемые того, какие бывают типы сечений конуса. Их четыре:

• Рассечь конус можно параллельно основанию, тогда при взгдяде на сечение мы увидим круг.
• Второй случай - параллельно оси конуса. В сечении получим гиперболу.
• Третий случай - параллельно образующей конуса. В сечении будет парабола.
• Четвертый случай, он же крайний - как раз наш пример, секущая плоскость наклонена под произвольным углом и не совпадает с первыми тремя частными случаями сечений. И вот в этом, четвертом случае, в сечении будет элипс.

Но если про элипс в сечении вы скорее всего знали, или догадывались, то вот насчет его центра очень многие ошибаются. Хотя казалось бы, поиск центра элипса в нашем случае не должен доставлять хлопот. Внимательно читаем и запоминаем: центр элипса в данном случае находится ровно посередине между точками 1 и 2. Поскольку 1-2 является одной из осей элипса. Большой или малой - зависит от наклона секущей плоскости и практического значения для нас сейчас не имеет.
Продолжим построения. Проведем через ту самую середину отрезка 1-2 вспомогательную секущую плоскость Q1. Как мы уже знаем, она как раз дает в сечении окружность при виде сверху. Обозначим ее:

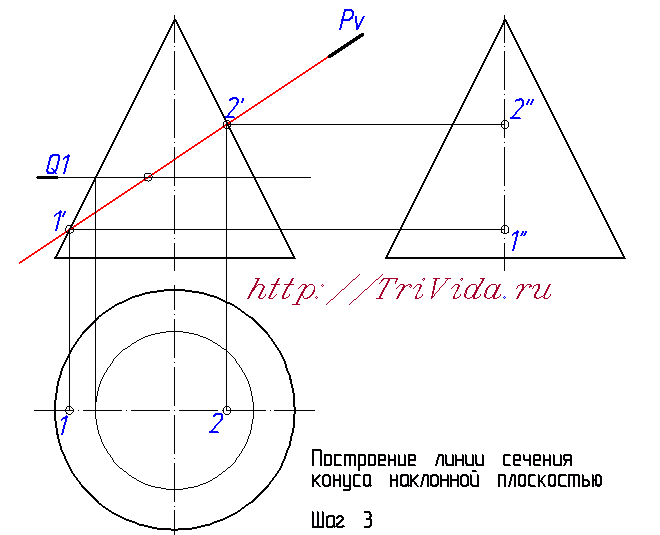
Обозначим точки пересечения этой вспомогательной плоскости Q1 с проекцией наклонной плоскости Pv на фронтальной проекци, получим точки 3' и 4'. Из них опускаем линию связи вниз, до пересечения с окружностью, получаем точки 3 и 4. Отрезок 3-4 является второй осью элипса.

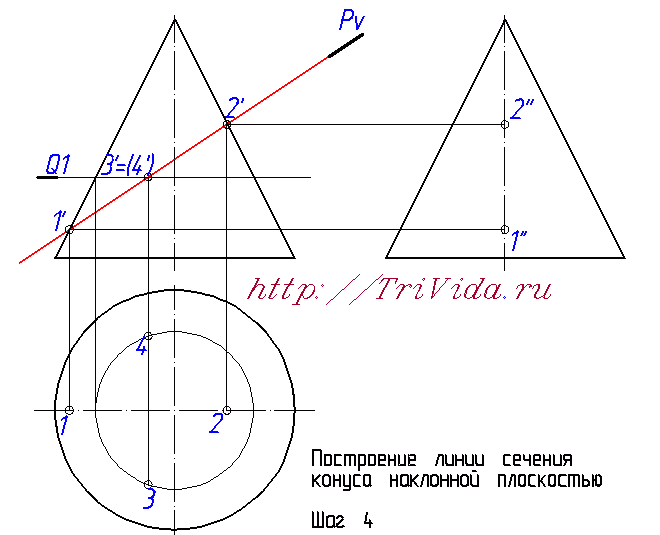
Чтобы построить профильные проекции этих точек, проводим из проекции точек 3' и 4' линию связи вправо, на профильную проекцию. И затем, на ней откладываем от оси конуса отрезки, обозначенные синим и зеленым цветом. Такой же длины, как синий и зеленые отрезки обозначенные на виде сверху (на горизонтальной проекции). Получаем точки 3" и 4".

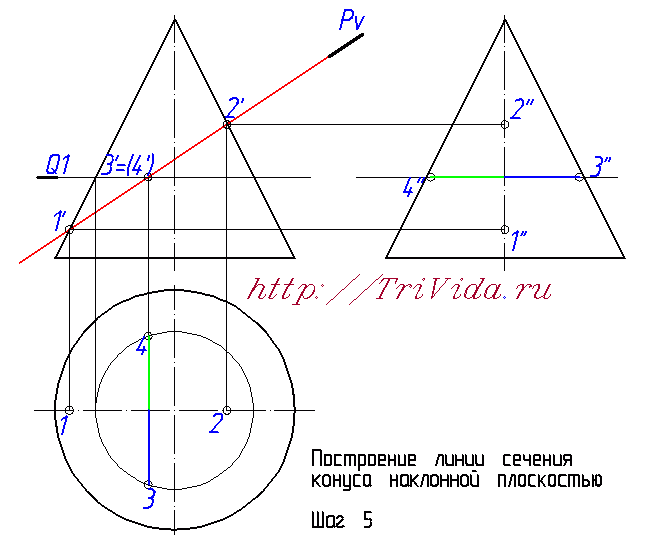
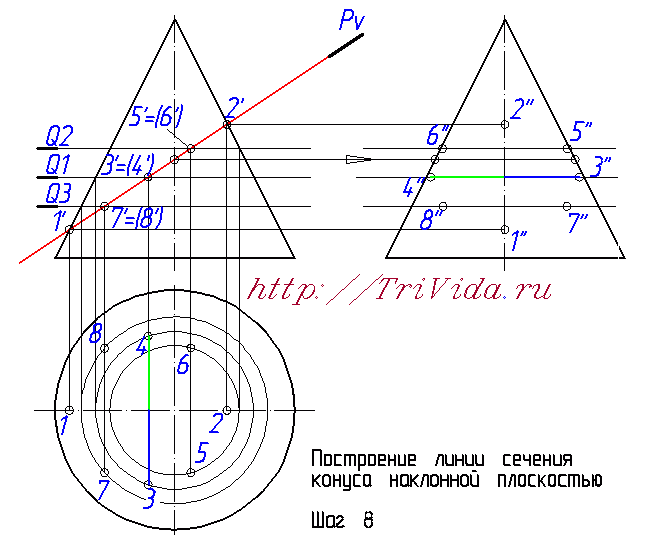
Математически на основе знаний о двух осях мы могли бы построить элипсы на горизонтальной и профильной проекциях. Но поскольку нам не удастся убедить преподавателя, что мы роботы, способные построить элипс опираясь только на 4 точки, мы вынуждены построить несколько дополнительных точек. На рисунке, изображающем 6-й шаг построения мы провели вспомогательную секущую плоскость Q2, в произвольном месте, где-то посередине между центром элипса и точкой 2'. C ее помощью (ориентируясь на алгоритм описанный при построении точек 3 и 4) определили все проекции точек 5 и 6.

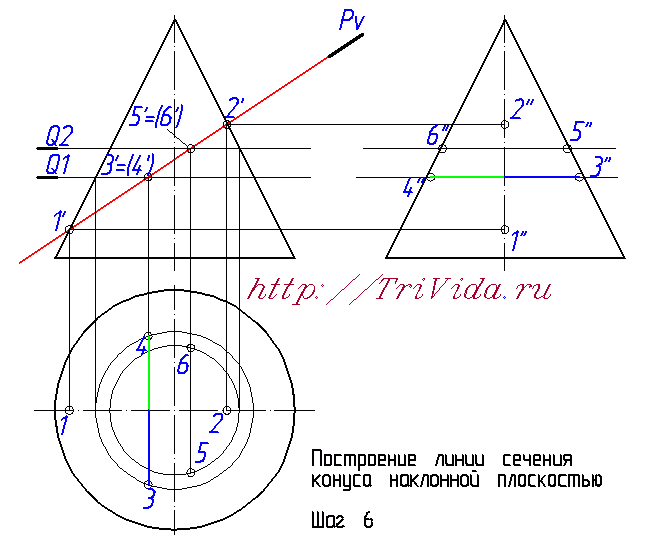
Точно так же проводим вспомогательную плоскость Q3 ниже точки 3' и выше точки 1' и с ее помощью находим все проекции точек 7 и 8. Теперь у нас уже есть 8 точек, чего вполне достаточно для более-менее точного построения от руки элипса не очень больших размеров. Если же у вас конус большой, то возможно вам имеет смысл провести еще некоторое количество вспомогательных секущих плоскостей и построить дополнительные точки.

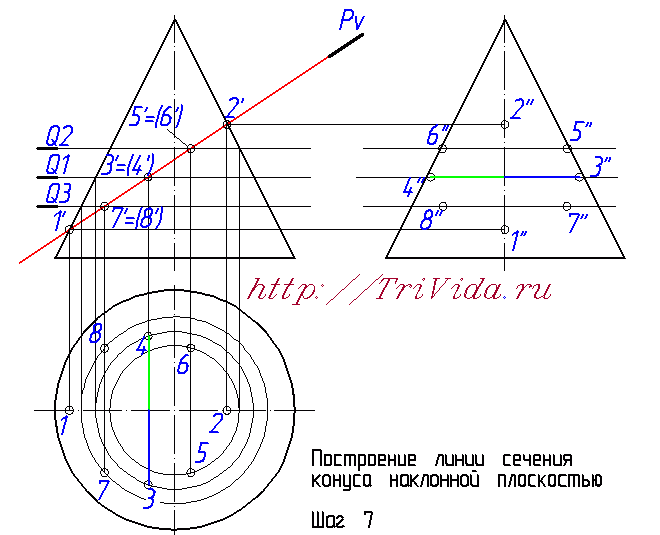
Остался еще один важный момент - определение точек границ видимости элипса на третьем виде. Для этого надо провести из точки пересечения плоскости Pv с осью элипса линию связи направо, на профильную проекцию. В местах, где эта диния пересекается с образующими конуса как раз и будут искомые точки. На чертеже я их никак не обозвал, вы же можете дать им имена 9" и 10". Та часть элипса, что будет за ними, будет находиться за конусом и соответственно будет невидидима.

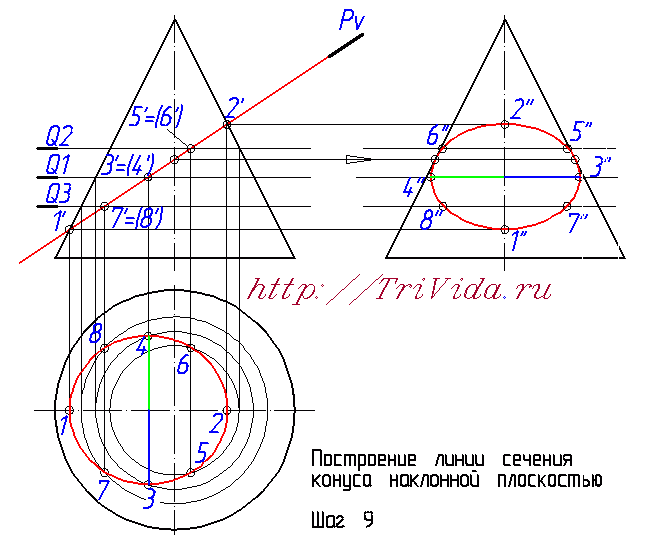
Проведем элипсы через полученные точки на горизонтальной и профильных проекциях:

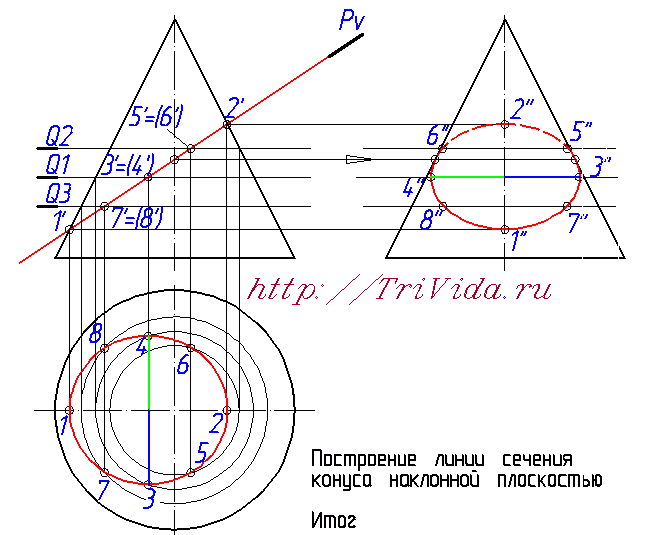
Последним этапом, завершающим построение линии пеерсечения Конуса с наклонной плоскостью, будет обозначение видимости элипса на профильной проекции:

Круглый стол

1 декабря 2014года, 15:30, аудитория 504

Модератор: Сучков М.А. – кандидат политических наук, преподаватель кафедры международных отношений, политологии и мировой экономики.

Председатель:Панин В.Н. - доктор политических наук, профессор.

Участники:

1) Белоконь А.Ю. – преподаватель кафедры международных отношений, политологии и мировой экономики;

2) Гукасов А.В. - кандидат политических наук, преподаватель кафедры международных отношений, политологии и мировой экономики;

3) Каширина Н.М. – доцент кафедры немецкого языка, преподаватель, сотрудник управления по формированию социальных компетенций, гражданскому воспитанию, подготовке выпускников к трудоустройству и будущей карьере;

4) Мхитарьян Г. – аспирант, сотрудник Волонтерского центра «ПРОФИ-СОЦИ-ЛИНГВА»;

5) Парастатов С.В. - кандидат политических наук, преподаватель кафедры международных отношений, политологии и мировой экономики;

6) Погорелова И.Ю. - кандидат филологических наук, преподаватель кафедры русской филологии;

7) Шабанова Е.А. – преподаватель кафедры конфликтологии, связей с общественностью и журналистики;

8) Альмова М. – студентка Института международных отношений;

9) Бициева Э. - студентка Института международных отношений;

10) Блинов В. – студент Института международных отношений;

11) Кауфов М. - студент Института международных отношений;

12) Плужников Д. - студент Института международных отношений;

13) Шанаева Э. - студентка Института международных отношений.