Полупроводники

Если валентная зона заполнена полностью, а расстояние до следующей свободной зоны мало, то такие твердые тела называются полупроводниками. При температуре Т=0 К валентная зона полупроводника заполнена целиком, а свободная зона пуста. Поэтому электропроводность полупроводника равна нулю. С повышением температуры часть электронов из валентной зоны переходит в свободную зону. При этом в валентной зоне появляются дырки. Количество тепловых забросов в зону проводимости пропорционально числу электронов вблизи верхнего края валентной зоны N_v , числу вакантных мест вблизи нижнего края свободной зоны N_c и вероятности того, что какой-либо электрон приобретет энергия ΔЕ, достаточную для перехода через запрещенную зону

,

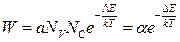где α-коэффициент пропорциональности. Чем больше ширина запрещенной зоны, тем меньше число забросов и тем меньше проводимость.

Одновременно с забросом электронов в зону проводимости происходит процесс рекомбинации – часть электронов падает из зоны проводимости в пустые места в валентной зоне. Число рекомбинаций в секунду пропорционально вероятности встречи электрона и дырки, т.е. числу электронов n и числу дырок р:

,

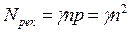где γ-постоянный коэффициент.

Так как в рассматриваемом случае количество дырок равно количеству электронов, то n=p. Если кристалл находится при данной температуре достаточно долго, то устанавливается равновесие, при котором количество забросов в зону проводимости равно числу актов рекомбинаций:

.

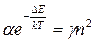Отсюда .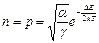

Согласно формуле (1) температурная зависимость электропроводности определяется температурными зависимостями концентрации носителей тока n(T) и их подвижности u(T):

.

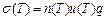В полупроводниках с повышением температуры концентрация носителей экспоненциально растет, а подвижность меняется по степенному закону:

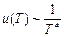, где

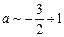
Поэтому температурная зависимость проводимости полупроводника в основном определяется температурной зависимостью концентрации носителей тока. Напротив, в металлах концентрация носителей от температуры не зависит. Поэтому температурная зависимость проводимости металлов обусловлена зависимостью подвижности от температуры.

Тогда для проводимости полупроводников можем записать:

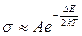, (5)

где А –постоянный коэффициент. Далее, логарифмируя обе части выражения, имеем:

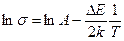(6)

Из выражения (6) видно, что зависимость lnσ = f(1/T) имеет линейный характер с тангенсом угла наклон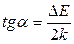

(рис.5). Из этого графика можно определить ширину запрещенной зоны полупроводника ΔЕ.