Приложение №2
Литература
2. Валуце И. И., Дилигул Г. Д. Математика для техникумов. Учебное пособие.-М.: Наука. Гл. ред. физ.-мат. лит., 1999г.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов.- М.: Наука, 1970-2001, т. 1,2.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс Высшей математики.- М.: Наука, 1989.
5. Данко П. Е., Попов А.Г., Кажевников Т.Я. Высшая математика в упражнениях и задачах. - М.:Наука,1999,ч.1,2
1.Основные понятия дифференциального уравнения.
Определение. Дифференциальное уравнения - это уравнение, связывающее функционально зависимые переменные и их производные.
Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Если искомая функция зависит только от одного аргумента, то уравнение называется обыкновенным.
Мы будем решать только обыкновенные дифференциальные уравнения.
В общем случае обыкновенное дифференциальное уравнение n–го порядка может быть записано в виде F(x, y, y/,y//...y(n))=0 , где y(x)- неизвестная функция, F-некоторая функциональная зависимость между независимой переменнойx, функцией y и её производными.
Например:
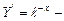 дифференциальное уравнение 1-го порядка,
дифференциальное уравнение 1-го порядка,
 - дифференциальное уравнение 2-го порядка,
- дифференциальное уравнение 2-го порядка,
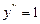 -дифференциальное уравнение 3-го порядка.
-дифференциальное уравнение 3-го порядка.
Определение: Функция, обращающая дифференциальное уравнение в тождество, называется решением этого уравнения.
2.Дифференциальные уравнения 1-го порядка с разделенными переменными.
В общем виде дифференциальное уравнение 1-го порядка можно записать как равенство F(x, y, y′) = 0
Дифференциальное уравнение вида f(x)dx = g(y)dy называют уравнением с разделёнными переменными.
Пример. Найти общее решение уравнения xdx+ydy=0
Решение.
Разделим переменные, запишем уравнение в виде xdx = -ydy
Проинтегрируем обе части уравнения, получим
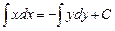 , или
, или 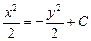 , или
, или 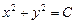 ,
, 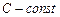 .
.
3.Дифференциальные уравнения 1-го порядка с разделяющими переменными.
Определение.Уравнением с разделяющимися переменными называется уравнение вида h(x)g(x) dx - 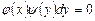
Чтобы привести это уравнение к уравнению с разделенными переменными достаточно разделить его на произведение 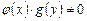
Пример.Найти общее решение уравнения y' = 3x – 1
Решение.
Представим производную у' как 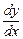 . Уравнение примет вид
. Уравнение примет вид 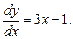
Чтобы разделить переменные, умножим обе части уравнения на dx. Полученное равенство проинтегрируем:
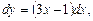
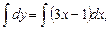
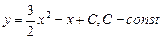
Ответ: 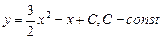 - общее решение.
- общее решение.
Пример.Найти решение уравнения y'+y-1=0.
Решение.
Запишем уравнение в виде: y' = 1 –y. Представим производную у' как 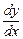 .
.
Уравнение примет вид 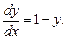 Умножим уравнение на dx и разделим на 1-y≠0. Получим уравнение с разделенными переменными:
Умножим уравнение на dx и разделим на 1-y≠0. Получим уравнение с разделенными переменными: 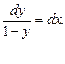
Найдём интегралы от обеих частей равенства:
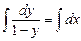
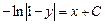 или
или 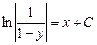
Ответ: 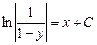 -решение дифференциального уравнения.
-решение дифференциального уравнения.
Пример.Найти общий интеграл (общее решение) уравнения

Вынесем за скобки общие множители: 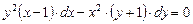
Теперь разделим обе части уравнения на (y2∙x2) и сократим на x2 и y2:
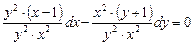 Получаем
Получаем 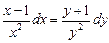
Проинтегрируем обе части отдельно: 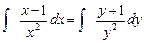
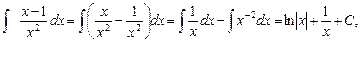
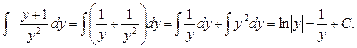
Общий интеграл (решение) уравнения имеет вид: 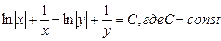
Преобразуем по свойству логарифмов и получим: 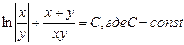
Ответ: 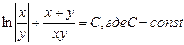 -решение уравнения.
-решение уравнения.
4.Однородные дифференциальные уравнения 1-го порядка
К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка.
Определение.Уравнение вида 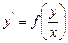 называется однородным дифференциальным уравнением 1-го порядка.
называется однородным дифференциальным уравнением 1-го порядка.
Такое уравнение подстановкой 

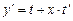 сводится к уравнению с разделяющимися переменными.
сводится к уравнению с разделяющимися переменными.
Пример.Найти общее решение дифференциального уравнения 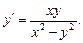
Решение.
Разделим правую часть уравнения (числитель и знаменатель) на x2. Получим уравнение 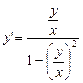 .
.
Выполним подстановки 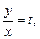
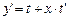 или в дифференциальной форме
или в дифференциальной форме 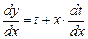 . После этого уравнение примет вид:
. После этого уравнение примет вид: 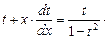
Перенесем t в правую часть и приведём дроби к общему знаменателю, то есть 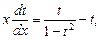
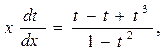
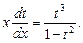
По основному свойству пропорции можно записать 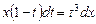 . Разделим обе части уравнения на (t3∙x) и получим
. Разделим обе части уравнения на (t3∙x) и получим 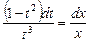 или
или 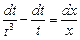 .
.
Проинтегрируем обе части равенства:
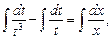
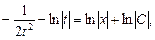
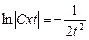
Выполним обратную подстановку  и получим общее решение дифференциального уравнения. Так как y = xt, то
и получим общее решение дифференциального уравнения. Так как y = xt, то 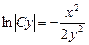 .
.
Выразим Cy, получим 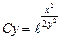
Ответ: 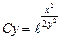
6.Линейные дифференциальные уравнения 1-го порядка
Определение.Линейным дифференциальным уравнением 1-го порядка называется уравнение относительно неизвестной функции и её производной 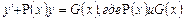 неизвестные функции.
неизвестные функции.
1)Если 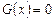 , то имеем частный случай, то есть
, то имеем частный случай, то есть 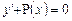 или
или 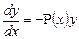
Это уравнение с разделяющимися переменными. Разделим переменные и выполним интегрирования отдельно каждой части уравнения:
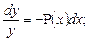
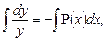
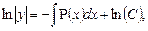
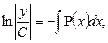
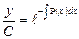 , следовательно,
, следовательно, 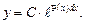
Если G(x)≠0, то уравнение 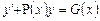 решается с помощью подстановки Бернулли y = u(x)∙v(x) или кратко y = uv. Подставим y = uv и
решается с помощью подстановки Бернулли y = u(x)∙v(x) или кратко y = uv. Подставим y = uv и 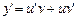 в уравнение, получим
в уравнение, получим 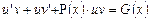
Сгруппируем слагаемые и получим уравнение 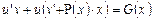 . Подберём функцию v так, чтобы выражение в скобках равнялось нулю 0. Тогда получим систему:
. Подберём функцию v так, чтобы выражение в скобках равнялось нулю 0. Тогда получим систему: 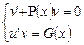 .
.
Теперь найдем v из первого уравнения системы (уравнение с разделяющимися переменными): 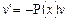 ,
, 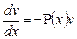 ,
, 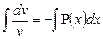 ,
,
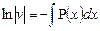 , получаем
, получаем 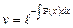 .
.
Подставим полученный результат во второе уравнение системы:
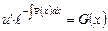 ,
, 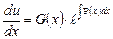 ,
,  .
.
Теперь находим общее решение исходного уравнения, как произведение u на v:
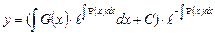

7.Дифференциальные уравнения 2-го порядка
Дифференциальные уравнения 2-го порядка в общем виде можно записать как
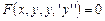 или
или 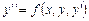
Линейным дифференциальным уравнением второго порядка называется уравнение вида  .
.
Если 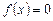 , то уравнение имеет вид
, то уравнение имеет вид 

Пример. Найти общее и частное решения дифференциального уравнения
y'' – 4y' + 13y = 0, y(0) = 1, y '(0) = 3
Решение. Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Составим и решим характеристическое уравнение:
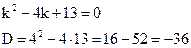
k1,2 = 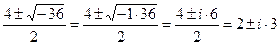
Тогда общее решение уравнения: у = e 2 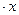 (C1 cos 3x +C2 sin 3x)
(C1 cos 3x +C2 sin 3x)
Для нахождения частного решения продифференцируем это выражение:
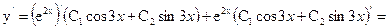
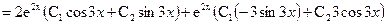
Из условий у(0) = 1, у'(0) = 3 находим
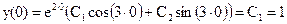
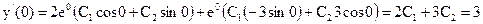
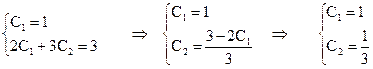
Поэтому частное решение данного дифференциального уравнения имеет вид:
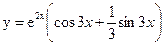
Ответ: 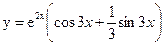
Приложение 1
Правила дифференцирования. Таблица производных и интегралов
Правила дифференцирования
| № | Функции | Производные |
| y = Cu | (Cu)' = C(u)' | |
| y = u ± v | (u ± v)' = u' ± v' | |
| y = u ∙ v | (u ∙ v)' = u'v + v'u | |
y = 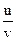
| 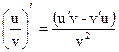
| |
| y = f(g(x)) | (f(g(x)))' = 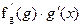
|
Производные элементарных функций
| (C)' = 0 | 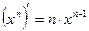
| ||
| (sin x) ' = cos x | (cos x) ' = - sin x | ||
(tg x) ' = 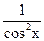
| (ctg x) ' = 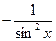
| ||
| (ex) ' = ex | (ax)' = axln(a) | ||
(lnx)' = 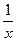
| 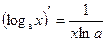
| ||
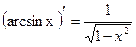
| 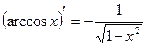
| ||
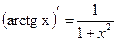
| 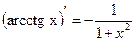
|
Неопределенные интегралы элементарных функций
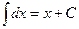
| 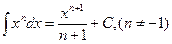
| ||

| 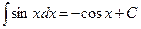
| ||
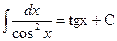
| 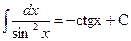
| ||
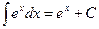
| 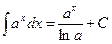
| ||

| 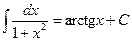
| ||
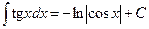
| 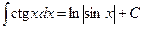
|
Приложение №2
Решить дифференциальные уравнения и выбрать правильный ответ:
1. 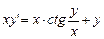
a) 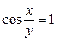 b)
b) 
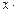
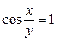 c) C
c) C 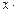
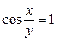
2. 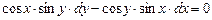
a)  b) cosy=C cosx c) y = C cosx
b) cosy=C cosx c) y = C cosx
3. 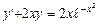
a) 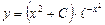 b)
b) 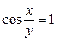 с) y=cosx
с) y=cosx
Верные ответы:
1. c) 2. b) 3. a)
Дата добавления: 2014-11-30; просмотров: 3492;
