Двигателя параллельного возбуждения

Механическая характеристика двигателя параллельного возбуждения жесткая, изменение скорости вращения двигателя при переходе от холостого хода к номинальной нагрузке мало

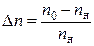100% ≈ (2…8)%.

С увеличением нагрузки скорость вращения двигателя уменьшается из-за увеличения падения напряжения в цепи якоря I_аR_а, но эта величина маленькая и скорость уменьшается незначительно. С увеличением тока якоря, растет размагничивающее действие реакции якоря, уменьшается магнитный поток Ф_δ и скорость увеличивается. Характеристика становится еще более жесткой (2), а при сильной реакции якоря может возрастать прямая (3). Такая характеристика неприемлема по условиям устойчивой работы.

Для обеспечения падающей характеристики в современных двигателях параллельного возбуждения на полюсах помещают слабую последовательную (стабилизирующую) обмотку W_ст = (1…3) витка для компенсации размагничивающего действия поперечной реакции якоря (прямая 1, рис. 1.72).

1.22.1. Условия устойчивости работы двигателя

Под устойчивостью работы двигателя нужно понимать его способность реагировать на внешние возмущения и способность вернуться к исходному, установившемуся режиму работы при прекращении действия этих возмущений.

Установившиеся режимы необходимы для реализации соответсвующих технологических процессов.

Опасность неустойчивой работы заключается в следующем.

1. Небольшие кратковременные возмущения вызывают колебательные режимы с возрастанием амплитуды колебаний тока и оборотов двигателя ( ).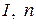

2. Небольшие кратковременные возмущения вызывают непрерывное и направленное изменение тока и оборотов двигателя ( 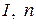и т.д ).

а) б)

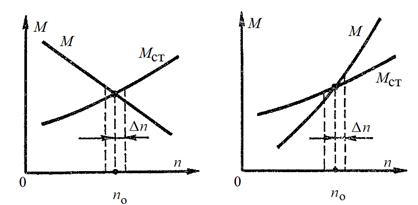
Рис. 1.73. Условия устойчивости работы двигателя

На рис. 1.73, а, б показаны два характерных случая работы двигателя, причем установившемуся режиму работы, когда 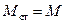со скоростью 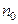соответствуетточка пересечения указанных двух характеристик.

Рассмотрим оба случая.

1. Когда зависимости 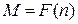и и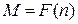меют вид, изображенный на рис. 4.6, а,то при действии возмущения и случайном увеличении при этом оборотов 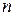на величину .

Тормозящий момент становится больше вращающегося (М < М_ст ), и двигатель будет затормаживаться и вернется в точку .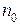

2. Если 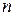уменьшится на , то, увеличивается вращающий момент(М > М_ст), двигатель ускоряется и вернется в точку .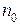

Работа двигателя будет устойчивой, ибо небольшие отклонения скорости вращения будут компенсироваться за счет взаимодействия характеристик движущего и тормозящего моментов.

При увеличении скорости М > М_ст и двигатель будет ускоряться, при уменьшении скорости М < М_ст, двигатель продолжает тормозиться.

Это позволяет вывести критерий устойчивости работы двигателя на основе анализа отношения приращений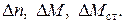

В первом случае 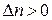, , 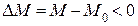отношение 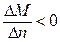(это следует из рис. 1.73). Одновременно 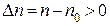и 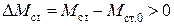, отношение 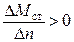. Условие устойчивости очевидно будет в виде неравенства .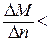

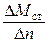Во втором случа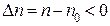е , , отношение .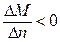

Одновременно 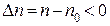и 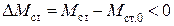, снова, как и в первом случае, отношение 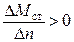. В итоге снова имеем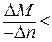 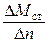. Если осуществить предельный переход при 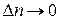, то получится условие устойчивости .

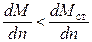Условие устойчивости можно назвать критерием, ибо оно выражено численной величиной.

Таким образом, критерием устойчивости работы двигателя является условие:

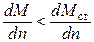(1.178)

Рассмотрим случай, изображенный на рис. 4.6.

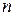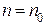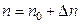1. При увеличении : до движущий момент будет больше тормозящего 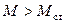. Возникнет избыток движущего момента, который будет направлен на дальнейшее увеличение скорости 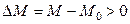. Одновременно будет иметь место положительное приращение 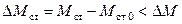, Отношение будет больше нуля 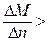0. отношение будет также больше нуля 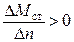, при этом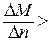 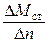будет условием неустойчивой работы двигателя.

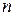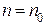2. При уменьшении от до 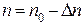движущий момент будет меньше тормозящего 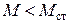. Возникнет избыток тормозящего момента, который будет направлен на дальнейшее уменьшение скорости 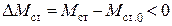. Одновременно будет иметь место отрицательное приращение движущего момента 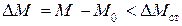, Отношение 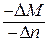будет больше нуля 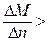0. Отношение 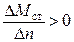будет также больше нуля, но при этом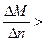 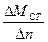будет условием неустойчивой работы. Если осуществить снова предельный переход при 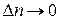, то получится условие неустойчивости работы двигателя

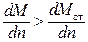. (1.179)