Общие сведения. При КЗ в сети через токоведущую часть аппарата могут проходить токи, в десятки раз превышающие номинальный ток

При КЗ в сети через токоведущую часть аппарата могут проходить токи, в десятки раз превышающие номинальный ток. Эти токи, взаимодействуя с магнитным полем, создают электродинамические силы, которые стремятся деформировать как сами проводники, так и изоляторы, на которых они крепятся.

Электродинамической стойкостью аппарата называется его способность противостоять силам, возникающим при прохождении токов КЗ.

Эта величина может выражаться либо непосредственно амплитудным значением тока 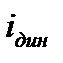, при котором механические напряжения в деталях аппарата не выходят за пределы допустимых значений, либо краткостью этого тока относительно амплитуды номинального тока.

.

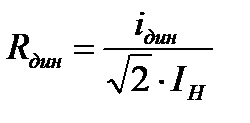Иногда динамическая стойкость оценивается действующим значением ударного тока за период после начала КЗ.

2.3.2. Методы расчёта электродинамических усилий (ЭДУ)

а) Методы расчёта.Для расчета э.д.у. используются два метода.

В первом – сила рассматривается как результат взаимодействия проводника с током и магнитного поля по правилу Ампера. Если элементарный проводник 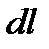с током 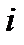находится в магнитном поле с индукцией 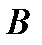, создаваемой другими проводниками (рис. 1), то сила 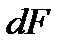, действующая на этот элемент, равна:

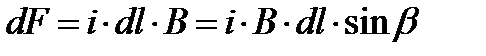
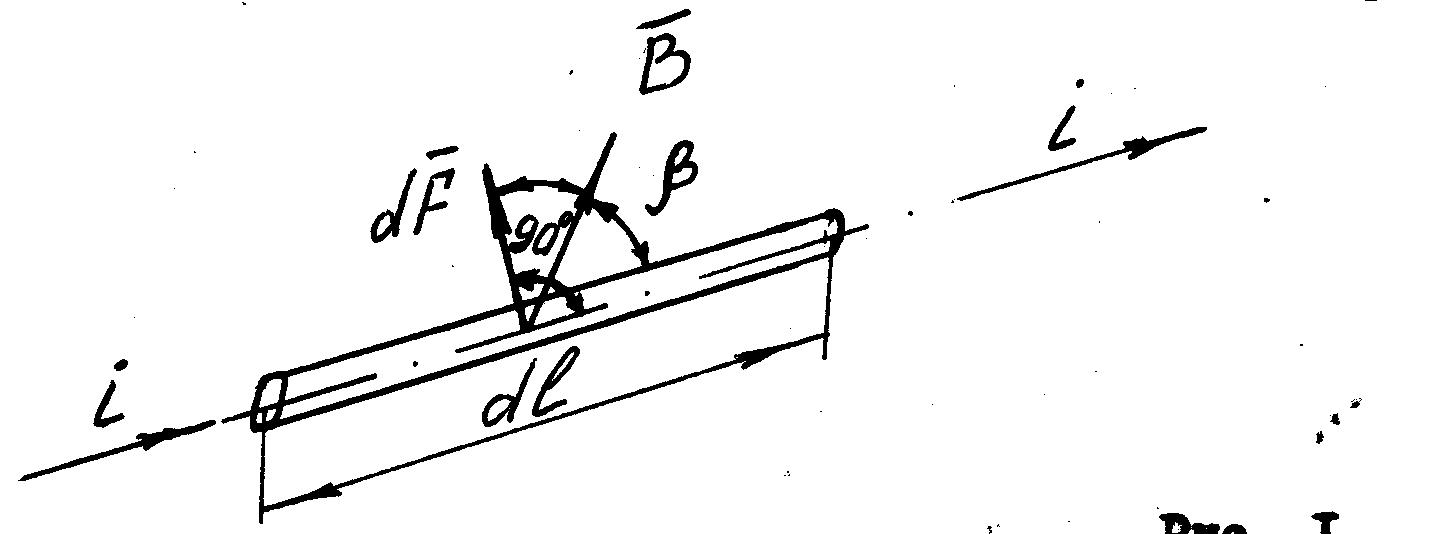
Рис. 1. Направление ЭДУ, действующего на элемент с током

где:

i – ток;

β – угол между векторами элемента dl и индукции B, измеряемый углом поворота вектора dl до вектора B по кратчайшему расстоянию.

За направление dl принимаем направление тока в элементе. Направление индукции B, создаваемой другим проводником, определяется по правилу Буравчика, а направление силы – по правилу левой руки.

Полная сила, действующая на проводник длиной l, определится по формуле

.

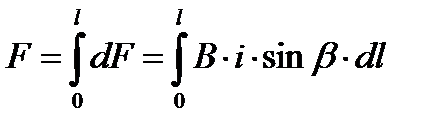В случае любого расположения проводников в одной плоскости β = 90°, то выражение имеет вид

.

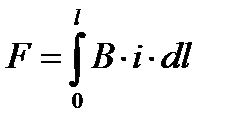Описанный метод рекомендуется применять тогда, когда можно аналитически найти индукцию в любой точке проводника, для которого необходимо определить силу.

Второй метод основан на использовании энергетического баланса системы проводников с током. Если пренебречь электростатической энергией системы и принять, что при деформации токоведущих контуров или при их перемещении под действием э.д.у. токи во всех контурах остаются неизменными, то силу можно найти по уравнению

,

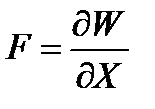где:

W - электромагнитная энергия;

X - возможное перемещение в направлении действия силы.

Электромагнитная энергия системы обусловлена как энергией магнитного поля каждого изолированного контура, так и энергией, определяемой магнитной связью между контурами, и для двух взаимосвязанных контуров равна:

,

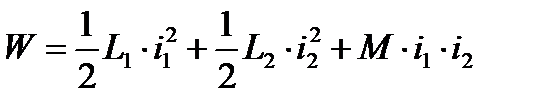где:

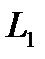и - и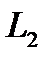ндуктивности контуров;

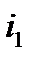и 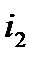- токи, протекающие в них;

М - взаимная индуктивность.

Первые два члена уравнения определяют энергию независимых контуров, а третий член дает энергию, обусловленную их магнитной связью.

Уравнение дает возможность рассчитать как силы, действующие в .изолированном контуре, так и силу взаимодействия контура со всеми остальными.

Для определения сил внутри одного независимого контура пользуемся уравнением

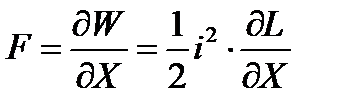
При расчете силы взаимодействия контуров мы считаем, что энергия изменяется только в результате изменения взаимного расположения контуров. При этом энергия, обусловленная собственной индуктивностью, считается неизменной. В данном случае, сила взаимодействия между контурами равна

.

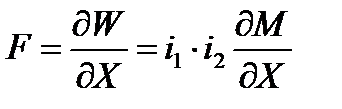Энергетический метод удобен, когда известна аналитическая зависимость индуктивности или взаимной индуктивности от геометрических размеров.

б) Направление действия ЭДУ.Найдем направление силы, действующей на элемент d1₁ с током 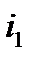, (рис.2).

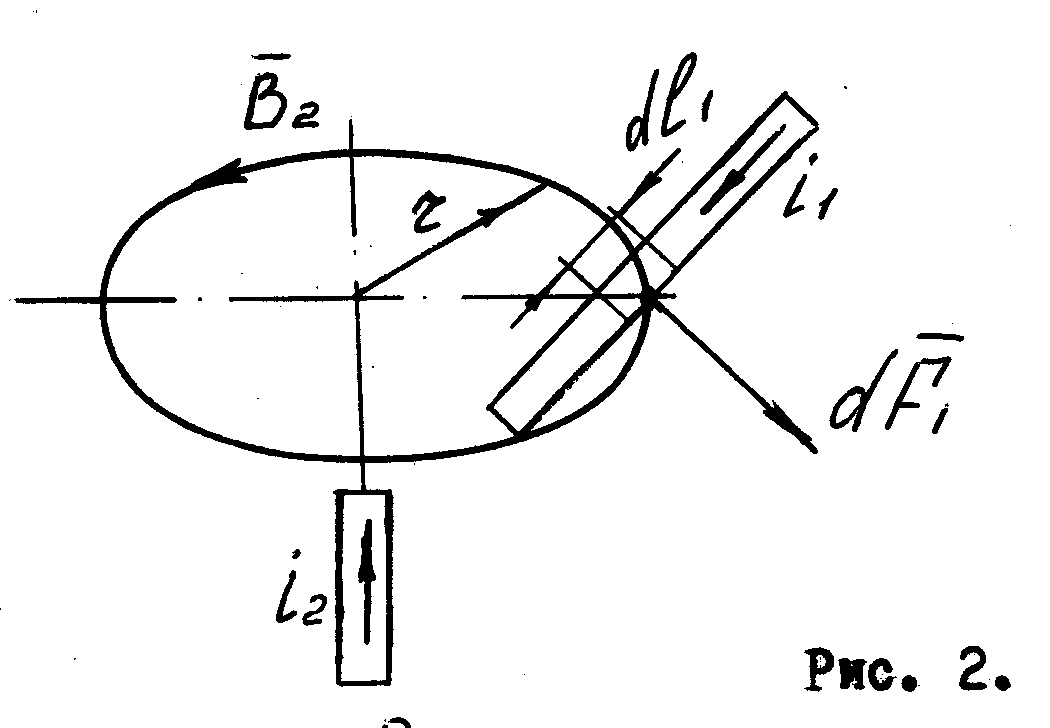
Рис. 2.

Линия индукции 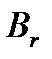, создаваемая током 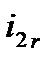, является окружностью с радиусом r, лежащей в плоскости, перпендикулярной 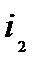. Направление силы dF определяется по правилу левой руки и показано на рис. 2.

Для плоской задачи, когда все проводники лежат в одной плоскости, результирующая на проводник, всегда перпендикулярна к этой плоскости, а сила лежит в плоскости. Направления э.д.у. для некоторых случаев расположения проводников в одной плоскости показаны на рис. 3.

Согласно положительному направлению силы соответствует возрастание энергии системы 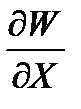, т. е. сила, действующая на токоведущие части, направлена так, чтобы электромагнитная энергия системы возрастала.

Для кольцевого контура

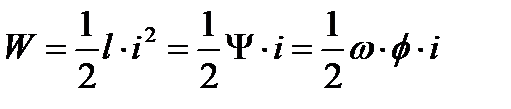
где:

ψ - потокосцепление;

Φ – поток;

ω - число витков в контуре.

В этом случае э.д.у. действует по радиусу, растягивая контур, т.к. при этом индуктивность, потокосцепление и поток возрастают.

В случае двух витков или катушек с разными направлениями токов сила F

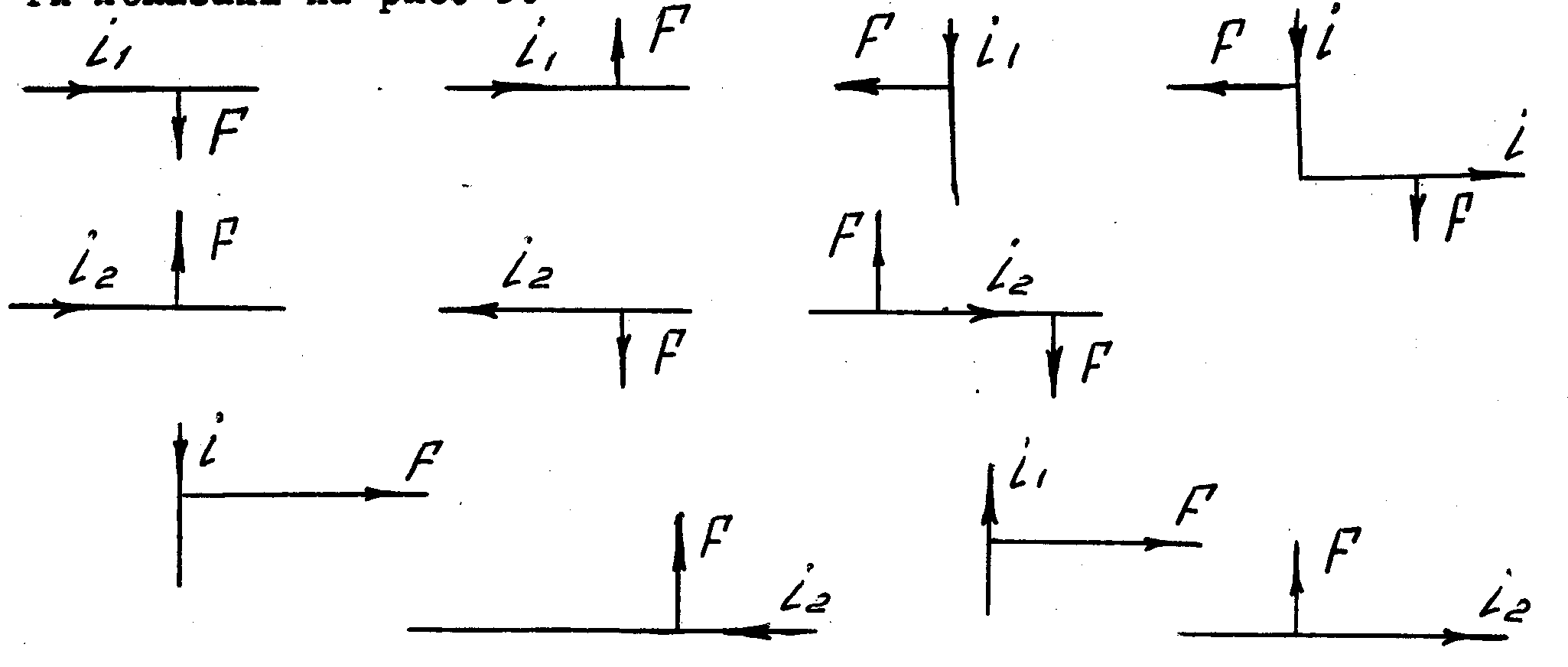
Рис. 3,

направлена так, чтобы отбросить витки друг от друга, т.к. потокосцепление увеличивается с ростом расстояния между ними. Минимальное потокосцепление будет иметь место при расстоянии между ними равном нулю. Если токи текут в одинаковом направлении, то витки притягиваются.