Противопоставление предикату
Это такое непосредственное умозаключение, при котором (в заключении) предикатом является субъект, субъектом — понятие, противоречащее предикату исходного суждения, и связка меняется на противоположную.
Его схема:
S есть Р.
не-Р не есть S.
Иными словами, мы делаем таким образом: 1) вместо Р берем не-Р;2) меняем местами S и не-Р;3) связку меняем на противоположную.
Например, дано суждение: «Все львы — хищные животные». В результате противопоставления предикату получим суждение: «Ни одно нехищное животное не является львом».
Противопоставление предикату можно рассматривать как результат двух последовательных непосредственных умозаключений — сначала превращения, затем обращения превращенного суждения.
Противопоставление предикату для различных видов суждений осуществляется так:
1. А. Все S есть Р.->Ни одно не-Р не есть S.
Все металлы электропроводны.-> Ни один не электропроводник не является металлом.
2. Е. Ни одно S не есть Р.-> Некоторые не-Р есть S.
Ни один красный мухомор не является съедобным грибом.-> Некоторые несъедобные грибы есть красные мухоморы.
3. О. Некоторые S не есть Р.-> Некоторые не-Р есть S.
Некоторые преступления не являются умышленными. -> Некоторые неумышленные деяния являются преступлениями.
4. I. Из частноутвердительного суждения необходимые выводы не следуют.
Задача
Сделать превращение, обращение и противопоставление предиката для следующего суждения: «Все грибы — растения».
Это суждение вида А.
Превращение — «Ни один гриб не является не растением».
Обращение (с ограничением) — «Некоторые растения являются грибами».
Противопоставление предикату — «Ни одно не растение не есть гриб».
Все виды непосредственных умозаключений дают нам новое знание, особенно умозаключение, называемое противопоставлением предикату.
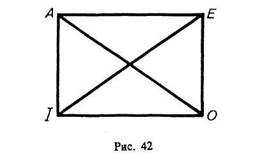
К непосредственным умозаключениям относятся и умозаключения по «логическому квадрату» (рис. 42).
В качестве примеров приведем такие суждения:
А — «Все свидетели дают истинные показания».
Е — «Ни один свидетель не дает истинные показания».
I— «Некоторые свидетели дают истинные показания».
О — «Некоторые свидетели не дают истинные показания».
Из истинности общего суждения следует истинность частного подчиненного ему суждения (т. е. из истинности А следует истинность I, из истинности Е следует истинность О). Относительно противоречащих суждений А — О и Е — I можно умозаключать так: если одно из них истинно, то другое обязательно ложно. Они подчиняются закону исключенного третьего.
§ 4. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ1
Категорический силлогизм — это вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, где S и Р связаны средним термином, при соблюдении правил необходимо следует заключение.
Силлогизм происходит от греческого syllogismos (сосчитывание, выведение следствия).
В составе категорического силлогизма имеются две посылки и заключение.
Все металлы (М) электропроводны (Р) — большая посылка.
Медь (S) есть металл (М) — меньшая посылка.
Медь (S) электропроводна (Р) — заключение.
Понятия, входящие в состав силлогизма, называются терминами силлогизма. В приведенном примере терминами являются: Р («электропроводник») — больший термин, это предикат заключения; S («медь») — меньший термин, это субъект заключения; М («металл») — средний термин, служащий в посылках для связывания S и Р и отсутствующий в заключении (рис. 43).
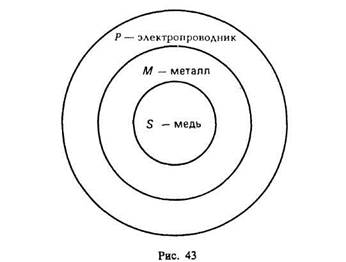
Посылка, содержащая предикат заключения (т. е. больший термин), называется большей посылкой. Посылка, содержащая субъект заключения (т. е. меньший термин), называется меньшей посылкой.
В основе вывода по категорическому силлогизму лежит аксиома силлогизма. «Все, что утверждается (отрицается) о роде (или классе), необходимо утверждается (отрицается) о виде (или о члене данного класса), принадлежащем к данному роду». Иными словами: то, что мы утверждаем о металле как роде, мы утверждаем и о его виде — меди, а именно утверждаем его признак «быть электропроводником».
Дата добавления: 2014-12-08; просмотров: 2485;
