КАК ИЗМЕРИТЬ УГОЛ?

Пусть в результате тщательного и искусного наблюдения та или шая цель вами найдена. Очевидно, этого еще мало: нужно определись местоположение цели, чтобы наша артиллерия знала, куда стрелять. Как это сделать?

Местоположение цели определяют обычно по отношению к ориентиру, — именно по отношению к тому ориентиру, который находится ближе всего к цели. Достаточно знать две координаты цели — ее дальность, то-естъ расстояние от наблюдателя или от орудия до цели, и угол, под которым цель видна нам правее или левее ориентира, — и тогда местоположение цели будет определено достаточно точно.

Предположим, ради простоты, что цель находится от нас на том же расстоянии, что и ориентир. Расстояние до этого ориентира нам известно заранее. Пусть оно равно 1000 метрам. Одна координата цели, следовательно, уже определена. Остается определить другую: угол между целью и ориентиром. Чем же и как артиллеристы измеряют углы?

В обыденной жизни вам не раз приходилось измерять углы: вы измеряли их в градусах и минутах. Артиллеристам же приходится не толшо измерять углы, но и быстро в уме по угловым величинам находить линейные величины и, наоборот, — по линейным величинам находить угловые. Пользоваться в таких случаях градусной системой измерения углов неудобно. Поэтому артиллеристы приняли совсем иную меру углов. Мера эта — «тысячная», или, как ее называют иначе, деление угломера.

Представим себе окружность, разделенную на 6000 равных частей.

Примем за основную меру для измерения углов одну шеститысячную долю этой окружности и попробуем определить ее величину в долях радиуса.

Известно, что радиус (R) любой окружности укладывается по ее длине приблизительно 6 раз, следовательно, можно считать, что длина окружности равна 6R. Мы же разделили окружность на 6000 равных частей; отсюда 6R = 6000 частей окружности. Теперь легко узнать, какую часть радиуса будет составлять одна шеститысячная часть окружности. Очевидно, что она будет в 6000 раз меньше величины 6R, то-есть будет равна 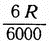или одной тысячной радиуса 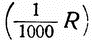. Поэтому-то артиллерийская мера углов — деление угломера — и носит название «тысячной» (рис. 212). Такой мерой пользоваться для измерения углов очень удобно. {243}

Вспомните, что в поле зрения бинокля вы видели сетку с делениями, то-есть короткие и длинные черточки, которые расположены вправо, влево и вверх от перекрестия, находящегося в центре поля зрения бинокля (рис. 213). Эти деления и есть «тысячные». Маленькое деление 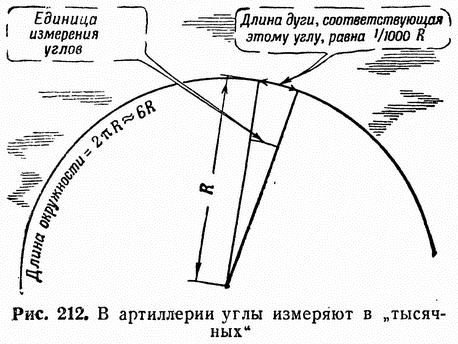сетки (между короткой и длинной черточками) равно 5 «тысячным», а большое деление (между длинными черточками) — 10 «тысячным».

На рис. 213 эти деления обозначены не просто числами 5 и 10, а с приставленными слева нолями — 6-05. и 0-10. Так пишут и произносят артиллеристы все угловые величины в «тысячных», чтобы избежать ошибок в командах. Например, если нужно передать в команде угол, равный 185 «тысячным» или 8 «тысячным», то произносят эти числа как номер телефона: «один восемьдесят пять» или «ноль ноль восемь», и соответственно пишут 1-85 или 0-08.

Зная теперь, как устроена сетка бинокля, вы можете измерить по ней угол между двумя предметами (точками местности), которые ввдны с вашего наблюдательного пункта. Взгляните опять на рис. 213. 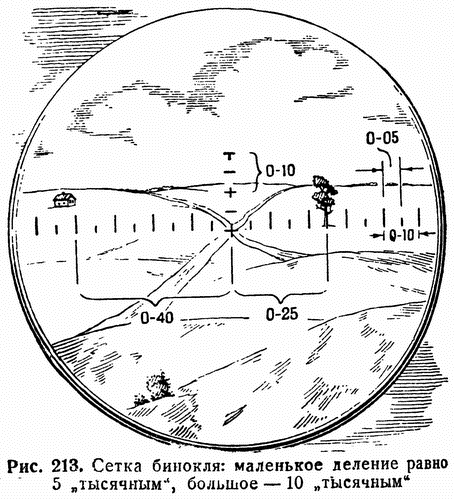Вы видите, что между перекрестком дорог, куда направлено перекрестие, и отдельно стоящим деревом (вправо от перекрестка дорог) укладывается два больших деления и одно маленькое, то-есть 25 «тысячных» или 0-25. Это и есть угол между перекрестком дорог и деревом. Точно так же вы можете определить угол между перекрестком дорог и домиком (влево от перекрестка дорог). Он равен 0-40. {244}

Сетка с делениями, примерно такая же как в бинокле, имеется и в поле зрения стереотрубы. Но у стереотрубы для измерения углов есть еще угломерная шкала снаружи.

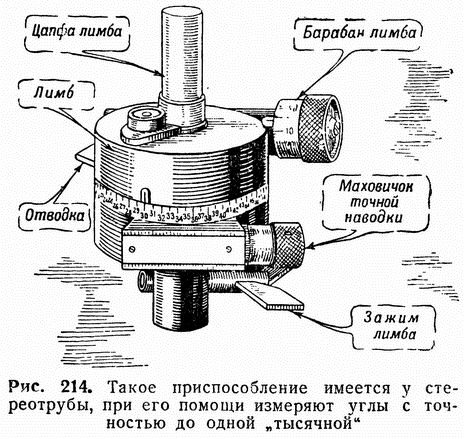На рис. 214 показаны те части стереотрубы (лимб и барабан лимба), при помощи которых можно более точно, чем по сетке, измерять горизонтальные углы.

Окружность лимба разделена на 60 частей, и поворот стереотрубы на одно деление лимба соответствует таким образом 100 «тысячным». Окружность же барабана лимба разделена на 100 частей, и при полном обороте барабана стереотруба поворачивается всего только на одно деление лимба (т. е. на 100 «тысячных»). Следовательно, деление барабана соответствует не 100 «тысячным», а всего лишь одной «тысячной». Это позволяет уточнять показания лимба в 100 раз и дает возможность измерять углы с точностью до одной «тысячной».

Чтобы измерить угол между двумя точками, пользуясь лимбом и барабаном, совмещают перекрестие стереотрубы сначала с правой тачкой; для этого, подведя указатель лимба к делению 30 и деление барабана 0 к его указателю (рис. 215), поворачивают трубу в нужную сторону при помощи маховичка точной наводки (см. рис. 214). Затем, вращая барабан лимба, совмещают перекрестие стереотрубы с левой точкой. При этом указатель лимба передвинется и покажет новый отсчет. Разность между полученным отсчетом и первоначальной установкой (30-00) и будет равна искомому углу (рис. 215).

Но не только при помощи этих сложных приборов можно измерять углы.

Ваша ладонь и ваши пальцы могут стать неплохим угломерным прибором, если только вы запомните, сколько в них заключается «тысячных» или, как говорят артиллеристы, какова «цена» ладони и пальцев. Хотя разные люди имеют разную ширину ладони и пальцев, но все же «цена» их не будет сильно отличаться от указанной на рис. 216. Вытянув перед собой руку на полную ее длину, вы можете быстро измерить угол между любыми точками местности (рис. 217). Чтобы не делать больших ошибок при измерении углов таким приемом, надо проверить «цену» своих пальцев. Для этого нужно вытянуть руку на уровне {245}

глаз и заметить, какую часть пространства закрыл собой палец (или ладонь руки), а затем измерить это пространство при помощи стереотрубы, поставленной на то же место.

Понятно, что подобным же простейшим «угломером» может служить всякий предмет, «цену» которого вы заблаговременно определили. На рис. 218 показаны такие предметы и их примерная «цена» в «тысячных».

Ознакомившись с приемами измерения углов, вы можете теперь убедиться в том, что, пользуясь «тысячными», можно весьма просто по угловым величинам определять линейные величины, а по линейным величинам — угловые. Для этого рассмотрим два примера. {246}

Первый пример (рис. 219). С наблюдательного пункта вы видите впереди проволочные заграждения противника; они протянулись полосой от мельницы влево до сухого дерева. Расстояние до мельницы, а следовательно, и до проволочных заграждений вы определили по карте; оно равно 1500 метрам. Вам поставлена задача — узнать длину наблюдаемой полосы проволочных заграждений. Как это сделать? Карта здесь вам не поможет, так как на ней нет сухого дерева, на ней есть только мельница.

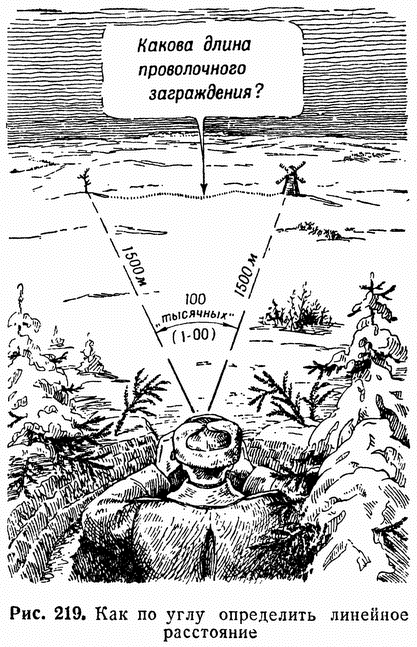Чтобы решить данную задачу, вы прежде всего определяете угол, под которым видна с наблюдательного пункта полоса проволочных заграждений, то-есть угол между направлениями на мельницу и на сухое дерево. Вы измерили этот угол по сетке бинокля; он оказался рашым 100 «тысячным», или 1-00.

Дальше задача решается просто. Надо лишь представить себе, что ваш наблюдательный пункт — это центр той окружности, которая описана радиусом, равным расстоянию от вас до мельницы. Радиус этот равен 1500 метрам. Углу в одну «тысячную» соответствует, как вы знаете, расстояние, равное одной тысячной радиуса, то-есть в данном случае 1,5 метра. А так как угол между мельницей и сухим деревом равен не одной, а 100 «тысячным», то значит расстояние между мельницей и сухим деревом равно не 1,5 метра, а 150 метрам. Это и будет длина полосы проволочных заграждений {247}

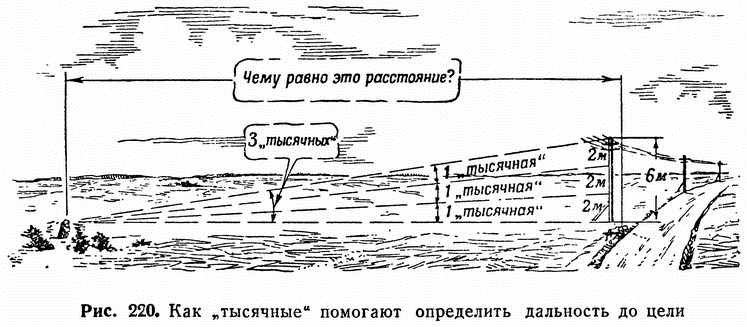
Второй пример (рис. 220). В канаве около шоссе вы обнаружили пулемет, по которому решили открыть огонь. Вам надо вычислить расстояние до пулемета или, что то же, — до шоссе.

Для решения этой задачи воспользуйтесь телеграфными столбами на шоссе; высота их известна — она равна 6 метрам. Измерьте теперь по вертикальной сетке бинокля угол, под которым вы видите телеграфный столб (угол между верхним концом столба и его основанием). Тогда вы будете иметь все данные для определения расстояния.

Допустим, что этот угол оказался равен 3 «тысячным». Очевидно, что если углу 3 «тысячных» с этого расстояния соответствует 6 метров на местности, то одной «тысячной» будет соответствовать 2 метра, а всему радиусу, то-есть расстоянию от вас до шоссе, будет соответствовать величина, в 1000 раз большая. Нетрудно сообразить, что расстояние от вас до шоссе будет равно 2000 метрам.

На рассмотренных примерах вы убедились, что принятая в артиллерии мера для измерения углов позволяет без всякого труда находить одну «тысячную» от любой величины расстояния. Для этого только надо в числе, выражающем величину расстояния, отделить справа три знака. Все это проделывается очень быстро в уме.

А вот что получилось бы, если за меру углов принять не «тысячную», а обычную, применяемую в геометрии меру углов: один градус или одну минуту. Углу в один градус соответствовала бы линейная величина, равная 1/60 радиуса, а углу в одну минуту — 1/3600 радиуса; следовательно, при решении любой из приведенных задач пришлось бы делить числа, выражающие расстояния до целей, не на 1000, а на 60 или на 3600.

Попробуйте проделать это деление с любым выбранным наугад числом и вы сейчас же убедитесь, что без карандаша и бумаги вам здесь не обойтись. Вот почему артиллерийская мера углов практически является несравненно более удобной. {248}