Ттттттттттт

Теңдеуді шешіңіз 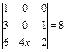Ж:2

Теңдеуді шешіңіз 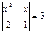Ж:

Теңдеуді шешіңіз 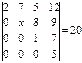Ж:2

Теңдеуді шешіңіз 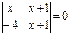Ж(-4;-1)

Теңдеуді шешіңіз 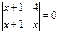Ж: (-1;4)

Теңдеуді шешіңіз 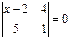Ж:22

Тетраэдрдің төбелері 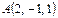, , 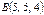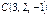және 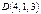нүктелерінде орналасқан. Осы тэтраэдрдің көлемін есептеңіз

Түзудің жалпы теңдеуін көрсет Ax+By+C=0

Түзудің кесінділік теңдеуін көрсет x\a+y\b=1

Түзудің параметрлік теңдеуін көрсет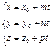

Түзудің канондық теңдеуін көрсет x-x₀\m=y-y₀\n=z-z₀\p

Төмендегі теңдіктердің қайсысы 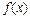функциясының қандай да бір 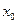нүктесіндегі үзіліссіздікті көрсетеді? lim

Туындыны табыңыз: 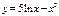5\x-2x

Туындысы арқылы функцияның өсу аралығын табыңыз: 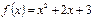[-1;∞)

Туындысы арқылы функцияның өсу аралығын табыңыз: 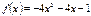(-∞;-1\2)

Туындысы арқылы функцияның өсу аралығын табыңыз: (-∞;∞)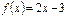

Туындысы арқылы функцияның өсу аралығын табыңыз: 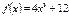[0;∞)

Туындысы арқылы функцияның өсу аралығын табыңыз: 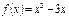(-∞;-1)U[1;∞)

У

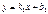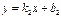және түзулерінің перпендикулярлық белгісін көрсет k₁k₂=1

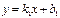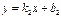және түзулерінің параллельдік белгісін көрсет k₁=k₂

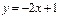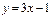және түзулерінің арасындағы сүйір бұрышты табыңыз 45⁰

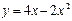параболасының төбесінің координаталарын табыңыз (1;2)

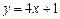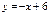және түзулерінің қиылысу нүктелерінің координаталарын табыңыз (1,5)

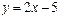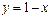және түзулерінің қиылысу нүктелерінің координаталарын табыңыз (2;-1)

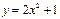функцияның анықталу облысын көрсетіңіз: (-∞;∞)

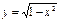функциясының анықталу облысын көрсетіңіз:[-1;1]

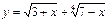функцияның анықталу облысын көрсетіңіз:[-3;7]

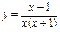функциясының үзіліс нүктесін көрсетіңіз: x=0,x=-1

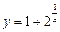функциясының үзіліс нүктесін табыңыз: х=0

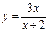функцияның үзіліс нүктесін және оның типін анықтаңыз: x=-2 π типті үзіліс

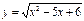функциясының анықталу облысын табыңыз: (-∞;2]U[3;∞)

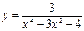функциясының үзіліс нүктесін табыңыз x₁=2, x₂=-2

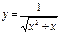функциясының үзіліс нүктесін табыңыз:x₁=0, x₂=-1

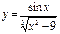функциясының үзіліс нүктесін табыңыз:x₁=3, x₂=-3

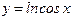функциясының анықталу облысын табыңыз:2πn-π\2<x<π\2+2πn

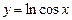функциясының мендер облысын табыңыз: y€(-∞;0)

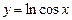функциясының периодын табыңыз: T=2π

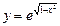функциясының анықталу облысын табыңыз: -1≤x≤1

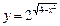функциясының мәндер облысын табыңыз: 1≤y≤4

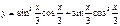функциясының периодын табыңыз:T=3π

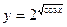функциясының периодын табыңыз: T=2π

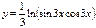функциясының периодын табыңыз: T=π\3

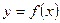функциясының 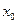нүктесiнде туындысы деп нені айтады? f^,(x₀)=limf(x₀+x)-f(x₀)\x

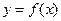функциясының 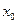нүктесiнде экстремумы болуы үшiн оның осы нүктедегi туындысы неге тең болады? нөлге тең (f^,(x₀)=0) н\е болмайды

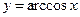функциясының туындысын көрсетіңіз: -1\√1-x²

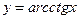функциясының туындысын көрсетіңіз: -1\1+x²

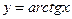функциясының туындысының формуласын көрсетіңіз 1\1+x²

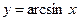функциясының туындысының формуласын көрсетіңіз: 1\√1-x²

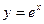функциясының туындысы неге тең? e^x

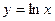функциясының туындысы неге тең? 1\x

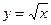функциясының туындысы неге тең? 1\2√x

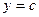туындысы, мұнда с-тұрақты 0

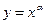туындысы неге тең? ax^a-1

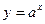туындысы неге тең? a^xlna

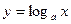туындысы неге тең? 1\xlna

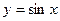туындысы неге тең? cosx

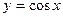туындысы неге тең? -sinx

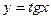туындысы неге тең? 1\cos²x

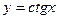туындысы неге тең? -1\sin²x

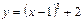функциясының иілу нүктесін табыңыз: (1;2)

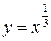функциясының иілу нүктесін табыңыз: (0;0)

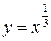функциясының кему аралығын табыңыз: (-∞;0)

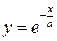функциясының 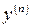табыңыз: (-1\a)^ae^-x\a

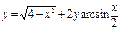функциясының туындысы 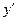-ті табыңыз: √2-x\√2+x

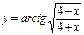функциясының 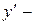табыңыз:-1\2 √16-x²

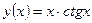функциясының табыңыз: ctgx-x\sin²x

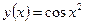функциясының табыңыз: -2xsinx²

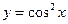функциясының табыңыз: -sin2x

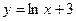функциясының туындысын табыңыз: 1\x

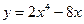функциясының 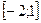кесіндісінде ең үлкен және ең кіші мәнін табыңыз: Y_max=48; Y_min=-6

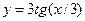функциясы берілген. 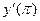-ді табыңыз: 4

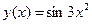функциясы берілген. 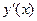- ді табыңыз: 6xcos3x²

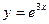функциясының төртінші ретті туындысын табыңыз: 81e^3x

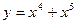функциясының алтыншы ретті туындысын табыңыз 0

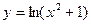функцияның екінші туындысын табыңыз: 2-2x²\(x²+1)²

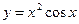функцияның туындысын табыңыз: 2xcosx-x²sinx

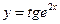функцияның туындысын табыңыз 2e^2x\cos²e^2x

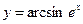функцияның туындысын табыңыз:e^x\√1-e^2x

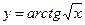функцияның туындысын табыңыз: 1\1+x*1\2√x

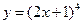функцияның туындысын табыңыз: 8(2x+1)³

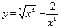функцияның туындысын табыңыз: 5\7*1\x^2\7+8\x⁵

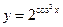функцияның туындысын табыңыз: -ln2*2cos²x*sin2x

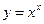функцияның туындысын табыңыз: x^x(lnx+1)

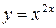функцияның туындысын табыңыз: 2x^2x(lnx+1)

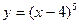функцияның иілу нүктесін көрсетіңіз: (4;0)

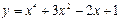функцияның туындысын табыңыз: 2(2x³+3x-1)

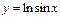функцияның туындысын табыңыз: ctgx

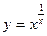функцияның туындысын табыңыз: x^1\x-2(1-lnx)

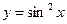функцияның үшінші ретті дифференциалын ( 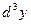) табыңыз: -4sin2x(dx)³

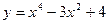функцияның үшінші ретті дифференциалын ( 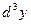) табыңыз: 24x(dx)³

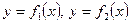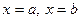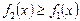, , сызықтарымен қоршалған жазық фигураның ауданы былай есептелінеді: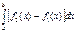

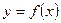қисығын 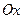( 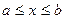) өсімен айналдырғаннан пайда болған дененіің көлемі былай есептелінеді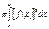

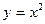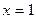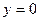, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек 1\3

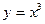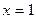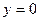, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек 1\4

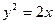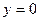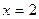, , сызықтарымен қоршалған жазық фигураның ауданын есеп 8\3

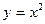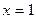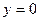, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

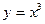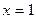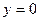, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек

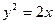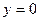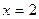, , сызықтарымен қоршалған жазық фигураның ауданын теу керек

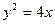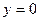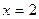, , сызықтарымен қоршалған жазық фигураның ауданын есептеу керек 8√2\3