Ееееееееееееее
Егер анықтауышта кейбір жолдың немесе бағанның элементтерінің ортақ көбейткіші болса, онда: оны анық. таңба.алдына шығар.
Егер бір матрица екінші бір матрицадан элементар (жәй) түрлендіру арқылы алынса, онда ол матрицалар: эквивалентті д.а.
Есептеңіз 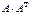


Егер 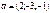 векторының ұшы
векторының ұшы 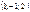 нүктесінде болса, онда осы вектордың басының координаталары неге тең? (-1,2,3)
нүктесінде болса, онда осы вектордың басының координаталары неге тең? (-1,2,3)
Егер 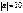 ,
,  ,
, 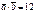 болса, онда
болса, онда  неге тең?16
неге тең?16
Егер 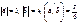 болса, онда
болса, онда 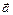 және
және  векторларына тұрғызылған параллелограммның ауданы 6
векторларына тұрғызылған параллелограммның ауданы 6
Егер  және
және 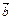 векторлары коллиенар болса, онда бір ғана
векторлары коллиенар болса, онда бір ғана 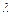 саны табылып мына теңдікті қанағаттандырады b=λa
саны табылып мына теңдікті қанағаттандырады b=λa
Егер  ,
, 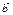 ,
, 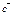 комплонар емес векторлар болса онда,
комплонар емес векторлар болса онда,  теңдігі келесі жағдайда ғана орындалады α=β=γ=0
теңдігі келесі жағдайда ғана орындалады α=β=γ=0
Егер  ,
, 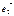 ,
,  векторлары кеңістіктегі базис болса, онда кез келген
векторлары кеңістіктегі базис болса, онда кез келген 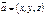 векторын бір ғана жолмен былай жіктеп жазуға болады a=xe1+ye2+ze3
векторын бір ғана жолмен былай жіктеп жазуға болады a=xe1+ye2+ze3
Егер  ,
,  болса, онда
болса, онда  тап 3
тап 3
Егер 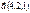 ,
,  векторлары берілсе, онда
векторлары берілсе, онда 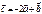 векторының координатасын табыңыз c=(-6.-7.-2)
векторының координатасын табыңыз c=(-6.-7.-2)
Егер  болса, онда
болса, онда 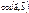 неге тең? 0
неге тең? 0
Егер  және
және 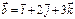 векторлары берілсе, онда
векторлары берілсе, онда 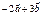 неге тең? -i+11k
неге тең? -i+11k
Егер  болса, онда
болса, онда  және
және 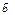 векторларына салынған параллелограмныңауданы неге тең?6
векторларына салынған параллелограмныңауданы неге тең?6
Егер  болса,
болса,  неге тең 16
неге тең 16
Егер 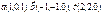 болса,
болса,  -ны табыңыз 0
-ны табыңыз 0
Егер  болса,
болса, 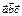 табыңыз 1
табыңыз 1
Егер  және
және  векторлары ортогонал және
векторлары ортогонал және  болса, онда
болса, онда 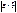 табыңыз 6
табыңыз 6
Егер 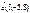 ,
, 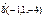 болса, онда
болса, онда  векторын табыңыз 2,-4,4
векторын табыңыз 2,-4,4
Егер 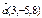 ,
, 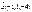 берілсе, онда
берілсе, онда 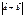 -ны табыңыз 6
-ны табыңыз 6
Егер  ,
, 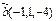 берілсе, онда
берілсе, онда  -ны табыңыз 14
-ны табыңыз 14
Егер  ,
, 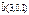 болса, онда
болса, онда  -ны табыңыз 36
-ны табыңыз 36
Егер  ,
,  ,
, 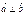 болса, онда
болса, онда  -ны табыңыз 12
-ны табыңыз 12
Екі  және
және  жазықтықтарының арасындағы бұрыш келесі формуламен есептелінеді: cosα=A1A2+B1B2+C1C2/(A12+B12+C12)(A22+B22+C22)
жазықтықтарының арасындағы бұрыш келесі формуламен есептелінеді: cosα=A1A2+B1B2+C1C2/(A12+B12+C12)(A22+B22+C22)
Екі 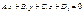 және
және 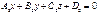 жазықтықтарының параллельдік белгісін көрсет A1/ A2= B1/ B2=C1/C2
жазықтықтарының параллельдік белгісін көрсет A1/ A2= B1/ B2=C1/C2
Екі  және
және  жазықтықтарының перпендикулярлық белгісін көрсет A1 A2+ B1 B2+ C1C2=0
жазықтықтарының перпендикулярлық белгісін көрсет A1 A2+ B1 B2+ C1C2=0
Екі  және
және 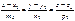 түзу. арасындағы бұрышты қайсы формуламен есептейді cosα=m1m2+n1n2+p1p2/(m12+n12+p12)(m22+n22+p12)
түзу. арасындағы бұрышты қайсы формуламен есептейді cosα=m1m2+n1n2+p1p2/(m12+n12+p12)(m22+n22+p12)
Екі  және
және  түзу.арасы. бұрыш келесі форм. есептелінеді: cosa=A1A2+B1B2\√A21+B21√A22+B22
түзу.арасы. бұрыш келесі форм. есептелінеді: cosa=A1A2+B1B2\√A21+B21√A22+B22
Екі  және
және 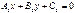 түзу. параллельдік белгісін көрсет A1/ A2= B1/ B2
түзу. параллельдік белгісін көрсет A1/ A2= B1/ B2
Екі  және
және 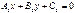 түзу. перпендикулярлық белгісін көрсет A1 A2+ B1B2 =0
түзу. перпендикулярлық белгісін көрсет A1 A2+ B1B2 =0
Екінші тамаша шекті көрсетіңіз: limx-∞(1+x)1/x=e
Екінші тамаша шекті көрсетіңіз: limx-∞(1+1\x)x=e
Егер 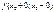 шектері бар, бірақ
шектері бар, бірақ 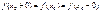 теңдіктерінің ең болмағанда біреуі орындалмаса, онда
теңдіктерінің ең болмағанда біреуі орындалмаса, онда 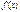 функциясы
функциясы  нүктесінде үзіледі
нүктесінде үзіледі
Егер екi рет дифференциалданатын 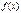 функциясының 1-шi ретті туындысы
функциясының 1-шi ретті туындысы  нүктесiнде 0-ге тең, ал екiншi туындысы
нүктесiнде 0-ге тең, ал екiншi туындысы 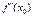 осы нүктеде оң болса, онда ол қандай нүкте болады? X0 min нүктесі
осы нүктеде оң болса, онда ол қандай нүкте болады? X0 min нүктесі
Егер екi рет дифференциалданатын 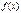 функциясының 1-шi ретті туындысы
функциясының 1-шi ретті туындысы 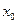 нүктесiнде 0-ге тең, ал 2-шi туындысы
нүктесiнде 0-ге тең, ал 2-шi туындысы 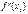 осы нүктеде терiс болса, онда онда ол қандай нүкте болады? X0 max нүктесі
осы нүктеде терiс болса, онда онда ол қандай нүкте болады? X0 max нүктесі
Екi рет дифференциалданатын  функциясының 2-шi ретті туындысының иiлу нүктесiндегi мәнi неге тең? 0
функциясының 2-шi ретті туындысының иiлу нүктесiндегi мәнi неге тең? 0
Екi рет дифференциалданатын  функциясының 2-шi ретті туындысы
функциясының 2-шi ретті туындысы  нүктесiнің маңайында таңбасын өзгеретiн болса, онда
нүктесiнің маңайында таңбасын өзгеретiн болса, онда 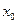 - қандай нүкте болады? функ.иілу нүктесі.
- қандай нүкте болады? функ.иілу нүктесі.
Егер 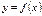 функциясы
функциясы  интервалында өспелі болса, онда бірінші туындысы қандай болады? f,(x)>0
интервалында өспелі болса, онда бірінші туындысы қандай болады? f,(x)>0
Егер 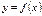 функциясы
функциясы 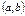 интервалында кемімелі болса, онда бірінші туындысы қандай болады?f,(x)<0
интервалында кемімелі болса, онда бірінші туындысы қандай болады?f,(x)<0
Егер  болса, онда
болса, онда 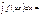 1\aF(ax)+C
1\aF(ax)+C
Егер 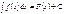 болса, онда
болса, онда 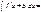 F(x+b)+C
F(x+b)+C
Егер  болса, онда
болса, онда  1\aF(ax+b)+C
1\aF(ax+b)+C
Егер  болса, онда
болса, онда  xm+1\m+1
xm+1\m+1
Егер  ,
,  болса, онда
болса, онда  ax\lna+C
ax\lna+C
Егер 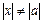 болса, онда
болса, онда 
Егер 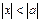 болса, онда
болса, онда 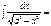
Егер 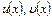 - дифференциалданатын функциялар болса, онда
- дифференциалданатын функциялар болса, онда 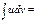
Егер  функциясы
функциясы  кесіндісінде интегралданса және
кесіндісінде интегралданса және  теңсіздігі орындалса, онда
теңсіздігі орындалса, онда 

Егер 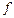 ,
, 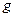 функциялары
функциялары 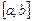 кесіндісінде интегралданса және
кесіндісінде интегралданса және 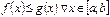 , онда
, онда 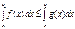
Егер  функциясы
функциясы 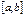 кесіндісінде үзіліссіз болса және
кесіндісінде үзіліссіз болса және  оның қайсыбір алғашқы функциясы болса, онда
оның қайсыбір алғашқы функциясы болса, онда 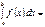 F(b)-F(a)
F(b)-F(a)
Егер  функциясы жұп болса, онда
функциясы жұп болса, онда 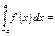

Егер  функциясы тақ болса, онда
функциясы тақ болса, онда 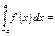 0
0
Егер  кесіндісінде параметрлік теңдеумен берілген
кесіндісінде параметрлік теңдеумен берілген  қисығында
қисығында  ,
,  функциялары үзіліссіз болса, онда
функциялары үзіліссіз болса, онда 

Егер  қисығы
қисығы  теңдеуімен берілсе, онда
теңдеуімен берілсе, онда 

Егер  қисығы поляр координат жүйесінде
қисығы поляр координат жүйесінде 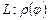 ,
, 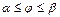 теңдеуімен берілсе, онда
теңдеуімен берілсе, онда 

Егер 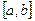 кесіндісінде
кесіндісінде 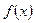 функциясының таңбалары шектеулі рет ауысса, онда
функциясының таңбалары шектеулі рет ауысса, онда 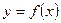 ,
, 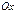 ,
, 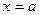 ,
, 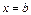 сызықтарымен қоршалған
сызықтарымен қоршалған  жазық фигурасының ауданы былай есептелінеді:
жазық фигурасының ауданы былай есептелінеді: 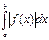
Егер x=1 болса, онда f(x)=(х2+1)\(х+1) функц.бірінші ретті туындысы мәнін таб.0,5
Ж
Жазықтықтың жалпы теңдеуін көрсет Ax+By+Cz+D=0
Жазықтықтың кесінділік теңдеуін көрсет x\a+y\b+z\c=1
Жарты өстері 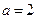 ,
, 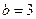 болған және төбесі Ох өсіне орналасқан гиперболаның теңдеуін жазыңыз x2\4-y2\9=1
болған және төбесі Ох өсіне орналасқан гиперболаның теңдеуін жазыңыз x2\4-y2\9=1
Дата добавления: 2014-12-06; просмотров: 1412;
