Гидростатика. Одним из главных физических выводов, основанных на наблюдениях природы, явился вывод о невозможности получения механической энергии ниоткуда

Одним из главных физических выводов, основанных на наблюдениях природы, явился вывод о невозможности получения механической энергии ниоткуда. Конечно, сейчас известны способы превращения иных форм энергии в механическую. Но эти формы энергии мы рассмотрим позднее. А пока обратимся, следуя Фейнману, к некоей механической машине, целью которой будет, например, поднятие более тяжелого груза за счет опускания более легкого. (Сам Фейнман придумал это рассуждение по аналогии с трудами Карно об обратимых тепловых машинах). Пусть наша машина поднимает три шарика на некоторую высоту х за счет опускания одного шарика на L.

Первоначально один шарик находился на высоте L, а три других – на высотах 0,х,2х. После опускания левого шарика, правые оказались на высотах х,2х,3х. Пусть наша машина работает без потерь энергии, сам рычаг тоже ничего не весит – то есть, наша машина идеальна. Чтобы она оказалась подготовлена к следующему циклу работы левый шарик нужно перекатить в положение правого нижнего (это можно сделать без затрат энергии – он не изменяет высоту), а правый верхний – в положение левого. Ну и опустить пустой рычаг, на что работы не требуется. Если 3x>L, мы выигрываем работу mg(3x-L) (правый шарик опускается), после чего система будет готова к следующему циклу. Вот и вечный двигатель! Значит неравенство 3x>L неверно. Может быть, 3x<L? Раз наша машина идеальна, ее можно заставить совершить процесс в обратном направлении

Видно, что при выполнении этого неравенства, машина также представляет собой вечный двигатель. Поэтому для идеальной машины 3x=L. Затраченная работа в точности равна полученной.

На этом утверждении базируется вся статика – наука о равновесии тел, условиях того, что они покоятся. Например, рычаг. Он будет находиться в равновесии при определенном соотношении масс на концах и длин плеч. Найдем условие равновесия.

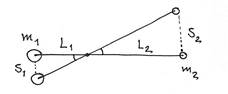
Слегка повернем рычаг вокруг горизонтальной оси. Груз m₁ опустится, и его потенциальная энергия уменьшится на m₁gs₁ . Если потенциальная энергия второго груза увеличится ровно на эту же величину, то кинетическая энергия грузов при этом перемещении не изменится. То есть, они не будут приходить в движение – система останется в покое, а перемещение в реальности не произойдет, оно мысленное (виртуальное). Хотя если мы в реальности повернем рычаг, то он перейдет в новое положение равновесия. Условие равновесия, полученное из условия, что полная работа силы тяжести равна 0, имеет вид

или

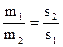
Из подобия треугольников поэтому

Вот и правило рычага. Очевидно, две силы, приложенные перпендикулярно к концам рычага, будут уравновешивать друг друга, если между ним выполняется соотношение

причем они должны закручивать рычаг в противоположных направлениях. Произведение силы на плечо L называется моментом силы. Для равновесия тела необходимо, чтобы не только сумма всех сил, приложенных к нему, была равна 0, но и сумма моментов этих сил.Момент силы берется со знаком +, если сила закручивает тело против часовой стрелки, и со знаком - , если по часовой стрелке. В общем случае, плечом силы называется длина перпендикуляра, опущенного из точки закрепления рычага на прямую, вдоль которой действует сила.

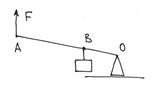Рычаги первого и второго рода

Разновидностью рычага является ворот.

Если систему тел удерживают в равновесии внешние силы, то вычислить их удобно следующим образом. Нужно придать системе малое перемещение, рассчитать работу внешних сил и приравнять ее к изменению потенциальной энергии системы. Таким же образом можно рассчитывать силы реакции, возникающие внутри системы, даже если реальные перемещения в системе невозможны (система жесткая). Вот почему этот принцип называется принципом виртуальных перемещений. Если работа внешней силы F_e на малом перемещении Dx равна изменению потенциальной энергии DW_p, то

Поскольку изменение потенциальной энергии не что иное, как работа внутренних сил системы, а они противоположны по знаку внешним силам, для внутренних сил в системе

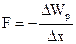
Применим ПВП к неподвижному и подвижному блокам.

В первом случае работа внешней силы FDx=mgDx. Поэтому F=mg для удержания или равномерного подъема груза на идеальном неподвижном блоке необходимо прикладывать силу, равную силе тяжести. Выигрыша в силе нет. Во втором случае подъем груза на Dx приводит к укорачиванию двух нитей, на которых висит подвижный блок каждой на Dx, поэтому правая нить удлиняется на 2Dx, что приводит к работе 2FDx= mgDx. Отсюда F= mg/2. Подвижный блок дает выигрыш в силе в два раза. Система подвижных и неподвижных блоков, называемая полиспастом, придуманная греками, может давать выигрыш в силе в десятки раз (Громов, Родина -7, стр 56, рис. 59)

Наклонная плоскость позволяет поднимать тела силой, меньшей, чем при вертикальном подъеме. Рассмотрим наклонную плоскость вдоль гипотенузы прямоугольного треугольника со сторонами 3L, 4L, 5L.

Какой груз необходимо использовать, чтобы уравновесить лежащий на плоскости груз 5m при отсутствии трения? Применим ПВП. Пусть груз 5m поднялся по плоскости, и его перемещение равно 5L. Неизвестный груз, висящий на нити, опустился на такую же высоту, совершив работу 5xgL. Но увеличение потенциальной энергии груза 5m составило 15mgL, поскольку он увеличил свою высоту на 3L. Приравнивая работы (что возможно лишь при отсутствии потерь на трение), получим 5xgL=15mgL, то есть x=3m. Стевин получил тот же вывод, рассматривая изящную систему, находящуюся в равновесии. Разновидностью наклонной плоскости является винт – можно сообразить, что это наклонная плоскость, навитая на цилиндр. Домкратпредставляет совокупность рычага и винта.

В жизни идеальных машин не бывает – это математические абстракции. Поэтому работа «на входе» машины (затрачиваемая) всегда больше работы «на выходе» (полезной). Часть затрачиваемой работы идет на преодоление сил трения (последнее слагаемое всегда отрицательно). Поэтому отношение 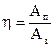всегда меньше единицы. Эту положительную безразмерную величину называют коэффициентом полезного действия механизма (КПД). КПД идеальных машин равно 1. Именно идеальные машины обладают свойством обратимости. Если подать на выход такой машины силы, снимаемые с нее при прямом цикле (совершить обратный ход), то со входа мы будем снимать силы, в точности равные силам, подаваемым на вход на прямом цикле.

Пример. Сложный блок представляет собой два блока радиусов r и R, насаженные на общую ось. Они не могут вращаться друг относительно друга. На них закреплена веревка, на которой висит подвижный блок с грузом m. Какую силу F нужно приложить к рычагу длиной L, связанному с осью, чтобы система не двигалась?

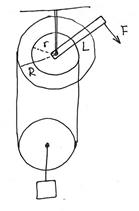Решим задачу методом ВП. Вначале нужно сообразить, в каком направлении должна действовать сила. Если верхний блок вращается по часовой стрелке, то наматываться будет больше нити, чем сматываться. Груз будет подниматься. Для этого нужно прикладывать силу по часовой стрелке, для удержания в равновесии – в том же направлении. Пусть конец рычага при небольшом повороте сместился на Dx, тогда с правой части блока смотается длина нити, равная 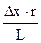, на левую часть намотается , таким образом, длина провисающей нити уменьшится на и груз поднимется на 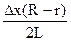. Приравнивая увеличение потенциальной энергии работе внешней силы 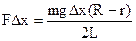, получим величину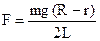

Гидростатика

Гидростатика изучает условия равновесия жидкостей. Как и в случае статики твердых тел мы рассматриваем неточечные тела. Поведение жидкостей и твердых тел отличается. При действии на них внешних сил, эти тела оказывают сопротивление. Видимо, внутри них происходят какие-то изменения в результате деформаций, что вызывает появление довольно больших сил реакции, препятствующих дальнейшему деформированию тел. Природу появления этих сил в механике не рассматривают. Однако, твердые тела и жидкости ведут себя по-разному. Твердое тело сохраняет свою форму, поэтому «сопротивляется» любым внешним силам. Жидкость же легко меняет свою форму, и лишь зафиксировав ее (поместив ее, например, в стакан) мы обнаружим, что сжать ее в стакане очень трудно.То есть, жидкость «сохраняет» свой объем, чтобы его изменить, нужно приложить большие усилия. Форма же жидкости, с условием сохранения объема, легко меняется небольшими силами.

Возьмем пластмассовый шприц и сделаем в его боковой стенке отверстие. Когда мы начнем сдавливать воду поршнем, то она будет вытекать не только из отверстия шприца (в направлении действия силы), но и из бокового отверстия (перпендикулярно направлению действия силы). То есть, внешнее воздействие передается во всех направлениях. Если на одном уровне в жидкости поместить три площадки равной площади, ориентированные по-разному, то силы давления на них будут одинаковы (но направлены по-разному, в направлении перпендикулярном площадкам).

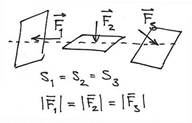
Поскольку давление есть отношение модуля силы к площади, то оно в жидкости на одном уровне будет одинаковым. Давление – скалярная величина, у него нет направления. Для определения силы давления мы должны знать не только давление, но и ориентацию площадки, на которую оно действует. На жидкость вблизи поверхности земли оказывает действие сила тяжести, поэтому давление в жидкости меняется с глубиной под действием собственной тяжести. Полное давление складывается из внешнего (например, атмосферного) и давления столба жидкости (гидростатического). Последнее вычисляется по формуле 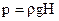(вывести самостоятельно!). Если бы жидкость была невесомой, то давление во всех ее точках было бы одинаковым. В этом и состоит закон Паскаля о том, что жидкость передает внешнее усилие по всем направлениям в равной мере. Полное давление на глубине Н равно 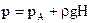, но ныряльщик «чувствует» только второе слагаемое, поскольку его внутреннее давление равно р_А. В воде на глубине 10 м добавочное давление столба жидкости становится равно атмосферному. В лабораторных опытах (например, в шприце) гидростатический столб мал по сравнению с прилагаемыми к жидкости внешними давлениями, поэтому закон Паскаля приближенно выполняется.

Гидростатический парадокс. Рассмотрим три легких стаканчика разной формы с одинаковой площадью дна. Отрежем донья и поставим два из них на весы. Нальем воду до одинаковой высоты. Позаботимся о том, чтобы жидкость не подтекала через щели между стаканами и чашами весов. Поскольку давления жидкостей и площади, на которые они действуют, одинаковы, то силы, действующие на чаши со стороны жидкостей должны быть одинаковыми. Так как сами стаканы легкие, то весы должны быть в равновесии. Но ведь силы тяжести, приложенные к жидкостям, различны. Весы не могут быть в равновесии. Посмотрев на рисунок ясно, почему. Жидкость оказывает добавочную силу давления на стенку стакана, которая и изменяет полную силу давления стакана с жидкостью на чашу.