Бахчиванжи Дарьи
При расчете числа Пи на CPU по результатам проделанной работы стало известно, что чем больше количество итераций, тем эффективнее работает параллельный алгоритм.
Самое эффективное – количество потоков = количеству ядер процессора.
На не больших количествах итераций система hyper-t не дает преимущества, за счет того, что потоки слишком быстро заканчивают свое действие. Но при более больших объемах вычислений, hyper-t позволяет и дальше увеличивать производительность поточного программирования, за счет удвоения числа реально работающих в параллельном режиме потоков, примерно на 20%.
На более высоких значениях количества итераций максимальное ускорение достигается на 8 потоках, из-за того, что данный процессор поддерживает технологию HyperThreading.
В процессорах с использованием этой технологии каждый физический процессор может хранить состояние сразу двух потоков, что для операционной системы выглядит как наличие двух логических процессоров (англ. Logical processor). Физически у каждого из логических процессоров есть свой набор регистров и контроллер прерываний (APIC), а остальные элементы процессора являются общими. Когда при исполнении потока одним из логических процессоров возникает пауза (в результате кэш-промаха, ошибки предсказания ветвлений, ожидания результата предыдущей инструкции), то управление передаётся потоку в другом логическом процессоре. Таким образом, пока один процесс ждёт, например, данные из памяти, вычислительные ресурсы физического процессора используются для обработки другого процесса.
Параллельные вычисления в целом более эффективнее, чем последовательные, из-за того, они используют всю вычислительную мощь процессора. Расчёты на GPU быстрее в 17 раз, чем на CPU.
Приложение 1
Код программы суммирование вектора GPU
#ifndef _COMMON_H
#define _COMMON_H
#define VECTOR_SIZE 8192
#define BLOCK_SIZE 512
#define BLOCKS (VECTOR_SIZE / BLOCK_SIZE)
extern "C" void reductionGPU(int *d_Dst, int *d_Src);
#endif
#include <cutil_inline.h>
#include "common.h"
__global__ void reductionKernel(int *d_Dst, int *d_Src)
{
__shared__ int data[BLOCK_SIZE];
int tid = threadIdx.x;
int idx = blockIdx.x * blockDim.x + threadIdx.x;
// Копируем из глобальной в локальную блоками
data[tid] = (idx < VECTOR_SIZE) ? d_Src[idx] : 0;
// Ждём пока каждый поток в блоке скопирует данные
__syncthreads ();
// Суммирование в параллели
for ( int s = blockDim.x / 2; s > 0; s >>= 1 )
{
if ( tid < s )
data[tid] += data[tid + s];
__syncthreads ();
}
// Первый поток в блоке записывает результат суммирования
if(tid == 0)
d_Dst[blockIdx.x] = data[0];
}
extern "C" void reductionGPU(int *d_Dst, int *d_Src)
{
reductionKernel<<<BLOCKS, BLOCK_SIZE>>>(d_Dst, d_Src);
cutilCheckMsg("convolutionRowsKernel() execution failed\n");
}
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#include <iterator>
#include <string.h>
#include <cutil_inline.h>
#include "common.h"
////////////////////////////////////////////////////////////////////////////////
// Main program
////////////////////////////////////////////////////////////////////////////////
int main(int argc, char **argv)
{
//Use command-line specified CUDA device, otherwise use device with highest Gflops/s
if ( cutCheckCmdLineFlag(argc, (const char **)argv, "device") )
cutilDeviceInit(argc, argv);
else
cudaSetDevice( cutGetMaxGflopsDeviceId() );
int *d_Input, *d_Output;
int* h_Input = new int[VECTOR_SIZE];
int* h_Output = new int[BLOCKS];
for(int i = 0; i < VECTOR_SIZE; ++i)
{
h_Input[i] = 1;
}
std::cout << "Size of data: " << VECTOR_SIZE << "\n";
std::cout << "Blocks: " << BLOCKS << "\n";
std::cout << "Allocating and initializing CUDA arrays...\n";
cutilSafeCall( cudaMalloc((void **)&d_Input, VECTOR_SIZE * sizeof(int)) );
cutilSafeCall( cudaMalloc((void **)&d_Output, BLOCKS * sizeof(int)) );
cutilSafeCall( cudaMemset(d_Output, 0x00, BLOCKS * sizeof(int)) );
cutilSafeCall( cudaMemcpy(d_Input, h_Input, VECTOR_SIZE * sizeof(int), cudaMemcpyHostToDevice) );
std::cout << "Running GPU reduction...\n";
cudaThreadSynchronize();
reductionGPU(d_Output, d_Input);
cudaThreadSynchronize();
std::cout << "Reading back GPU results...\n";
cutilSafeCall( cudaMemcpy(h_Output, d_Output, BLOCKS * sizeof(int), cudaMemcpyDeviceToHost) );
std::cout << "Results: \n";
std::copy(h_Output, h_Output + BLOCKS, std::ostream_iterator<int>(std::cout,", "));
cutilSafeCall( cudaFree(d_Input) );
cutilSafeCall( cudaFree(d_Output) );
delete[] h_Input;
delete[] h_Output;
cudaThreadExit();
cutilExit(argc, argv);}
Технический вывод программы
Size of data: 8192
Blocks: 16
Allocating and initializing CUDA arrays...
Running GPU reduction...
Reading back GPU results...
Results:
512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512, 512
Press ENTER to exit...
Код программы суммирование вектора CPU
#include <iostream>
#include <ctime>
#include <vector>
#include <algorithm>
#include <iterator>
void show (const std::vector <float> &);
int main (void)
{
const int SIZE=5;
std::vector <float> A;
std::vector <float> B;
std::vector <float> REZULT (SIZE);
float tmp;
// fill vector A
for (int i=0; i<SIZE; i++) {
std::cout << "A[" << i <<"]: ";
std::cin >> tmp;
A.push_back (tmp); }
// fill vector B
for (int i=0; i<SIZE; i++) {
std::cout << "B[" << i <<"]: ";
std::cin >> tmp;
B.push_back (tmp); }
//
std::vector <float> :: iterator A_=A.begin();
std::vector <float> :: iterator B_=B.begin();
std::vector <float> :: iterator REZULT_=REZULT.begin();
for (REZULT_; REZULT_!=REZULT.end(); REZULT_++, A_++, B_++)
*(REZULT_)=*(A_) + *(B_);
time = clock() - time;
// output
std::cout << "Vector A: ";
show (A);
std::cout << "Vector B: ";
show (B);
std::cout << "Vector REZULT: ";
show (REZULT);
system ("pause");
return 0;
}
void show (const std::vector <float> &vec)
{
std::copy (vec.begin(), vec.end(), std::ostream_iterator <int> (std::cout, " "));
std::cout << std::endl;
}
Код программы расчёта БПФ с использованием библиотеки jCuda
public class JCufftDemo {
public static void main(String[] args) {
double[] fftResults;
int dataSize = 1<<23;
System.out.println("Генерация входных данных размером "+dataSize+" значений...\n");
float[] inputData = createRandomData(dataSize)
System.out.println("1D БПФ с использованием apache commons math...");
fftResults = commonsTransform(floatDataToDoubleData(inputData.clone()));
printSomeValues(fftResults);
System.out.println();
System.out.println("1D БПФ JCufft (данные в оперативной памяти)...");
fftResults = jcudaTransformHostMemory(inputData.clone());
printSomeValues(fftResults);
System.out.println();
System.out.println("1D БПФ JCufft (данные в памяти видеокарты)...");
fftResults = jcudaTransformDeviceMemory(inputData.clone());
printSomeValues(fftResults);
}
/**
* Генерирует массив случайных чисел
*
* @param dataSize - размер генерируемого массива
* @return массив случайных чисел
*/
public static float[] createRandomData(int dataSize){
Random random = new Random();
float data[] = new float[dataSize];
for (int i = 0; i < dataSize; i++)
data[i] = random.nextFloat();
return data;
}
/**
* Конвертирует массив значений типа float в массив значений double
*
* @param data - массив который нужно конвертировать
* @return - сконвертированный массив
*/
public static double[] floatDataToDoubleData(float[] data){
double[] doubleData = new double[data.length];
for(int i=0; i < data.length; i++) doubleData[i] = data[i];
return doubleData;
}
/**
* Выполняет БПФ массива значений с помощью CUDA, осуществляя
* операции с данными в оперативной памяти
*
* @param inputData - массив входных значений
* @return массив с результатами БПФ
*/
public static double[] jcudaTransformHostMemory(float[] inputData){
float[] fftResults = new float[inputData.length + 2];
// создание плана
cufftHandle plan = new cufftHandle();
JCufft.cufftPlan1d(plan, inputData.length, cufftType.CUFFT_R2C, 1);
// выполнение БПФ
long timeStart = new Date().getTime();
JCufft.cufftExecR2C(plan, inputData, fftResults);
System.out.println("Время преобразования: " + (new Date().getTime() - timeStart)/1000.0+" сек");
// уничтожение плана
JCufft.cufftDestroy(plan);
return cudaComplexToDouble(fftResults);
}
/**
* Выполняет БПФ массива значений с помощью CUDA, осуществляя
* операции с данными в памяти видеокарты
*
* @param inputData - массив входных значений
* @return массив с результатами БПФ
*/
public static double[] jcudaTransformDeviceMemory(float[] inputData){
float[] fftResults = new float[inputData.length + 2];
// указатель на устройство
Pointer deviceDataIn = new Pointer();
// выделение памяти на видеокарте для входных данных
JCuda.cudaMalloc(deviceDataIn, inputData.length * 4);
// копирование входных данных в память видеокарты
JCuda.cudaMemcpy(deviceDataIn, Pointer.to(inputData), inputData.length * 4,
cudaMemcpyKind.cudaMemcpyHostToDevice);
Pointer deviceDataOut = new Pointer();
// выделение памяти на видеокарте для результатов преобразования
JCuda.cudaMalloc(deviceDataOut, fftResults.length * 4);
// создание плана
cufftHandle plan = new cufftHandle();
JCufft.cufftPlan1d(plan, inputData.length, cufftType.CUFFT_R2C, 1);
/*
*plan - указатель на план
*inputDataSize - количество входных значений; если входные данные являются *вещественными, то этот параметр равняется длине входного массива, а если *входные данные это массив комплексных чисел, то значение параметра равно *половине длины входного массива, т.к. одно комплексное число представлено *двумя элементами массива
*cufftType.CUFFT_R2C - тип преобразования
*1 - количество подобных преобразований
*/
// выполнение БПФ
long timeStart = new Date().getTime();
JCufft.cufftExecR2C(plan, deviceDataIn, deviceDataOut);
System.out.println("Время преобразования: " + (new Date().getTime() - timeStart)/1000.+" сек")
// копирование результатов из памяти видеокарты в оперативную память
JCuda.cudaMemcpy(Pointer.to(fftResults), deviceDataOut, fftResults.length * 4,
cudaMemcpyKind.cudaMemcpyDeviceToHost);
// освобождение ресурсов
JCufft.cufftDestroy(plan);
JCuda.cudaFree(deviceDataIn);
JCuda.cudaFree(deviceDataOut);
return cudaComplexToDouble(fftResults);
}
/**
* Выполняет БПФ массива значений с помощью Apache Commons Math
*
* @param inputData - массив входных значений
* @return массив с результатами БПФ
*/
public static double[] commonsTransform(double[] inputData){
FastFourierTransformer fft = new FastFourierTransformer();
long timeStart = new Date().getTime();
Complex[] cmx = fft.transform(inputData);
System.out.println("Время преобразования: " + (new Date().getTime() - timeStart)/1000.+" сек");
double[] fftReults = new double[inputData.length/2 + 1];
for(int i = 0; i < fftReults.length; i++){
fftReults[i] = cmx[i].abs();
}
return fftReults;
}
/**
* Метод осуществляет преобразование массива комплексных чисел в
* массив, содержащий их модули
*
* @param complexData - массив комплексных чисел
* @return массив модулей комплексных чисел
*/
public static double[] cudaComplexToDouble(float[] complexData){
double[] result = new double[complexData.length/2];
int j=0;
for(int i=0; i < complexData.length-1; i++) {
result[j++] = Math.sqrt(complexData[i]*complexData[i] + complexData[i+1]*complexData[i+1]);
i++;
}
return result;
}
/**
* Выводит на стандартный вывод первое, среднее
* и последнее значения массива
*
* @param data - массив, значения которого необходимо вывести
*/
public static void printSomeValues(double[] data){
System.out.println("[0]: "+data[0]);
System.out.println("["+(data.length/2)+"]: "+data[data.length/2]);
System.out.println("["+(data.length-1)+"]: "+data[data.length-1]);
}
}
Технический вывод программы
Генерация входных данных размером 8388608 значений...
1D БПФ с использованием apache commons math...
Время преобразования: 92.851 сек
[0]: 4195107.645827353
[2097152]: 1411.8392665442454
[4194304]: 114.60465306043625
1D БПФ JCufft (данные в оперативной памяти)...
Время преобразования: 0.085 сек
[0]: 4195107.922955976
[2097152]: 1411.791370918522
[4194304]: 114.75
1D БПФ JCufft (данные в памяти видеокарты)...
Время преобразования: 0.0 сек
[0]: 4195107.922955976
[2097152]: 1411.791370918522
[4194304]: 114.75
Код программы расчёта числа PI
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <conio.h>
#include <time.h>
#include <cuda.h>
#include <math.h>
#include <Windows.h>
#define CUDA_FLOAT float
const long GRID_SIZE=1024;
const long BLOCK_SIZE=16;
__global__ void pi_kern(CUDA_FLOAT *res)
{
int n = threadIdx.x + blockIdx.x * BLOCK_SIZE;
CUDA_FLOAT x0 = n * 1.f / (BLOCK_SIZE * GRID_SIZE); // Началоотрезка интегрирования
CUDA_FLOAT y0 = sqrtf(1 - x0 * x0);
CUDA_FLOAT dx = 1.f / (1.f * BLOCK_SIZE * GRID_SIZE); // Шагинтегрирования
CUDA_FLOAT s = 0; // Значение интеграла по отрезку, данномутекущему треду
CUDA_FLOAT x1, y1;
x1 = x0 + dx;
y1 = sqrtf(1 - x1 * x1);
s = (y0 + y1) * dx / 2.f;// Площадь трапеции
res[n] = s;// Запись результата в глобальную память
}
int main(int argc, char** argv)
{
clock_t time;
CUDA_FLOAT *res_d;// Результаты на устройстве
CUDA_FLOAT res[GRID_SIZE * BLOCK_SIZE];// Результаты в хостовой памяти
cudaMalloc((void**)&res_d, sizeof(CUDA_FLOAT) * GRID_SIZE *
BLOCK_SIZE);// Выделение памяти на CPUл
// Рамеры грида и блока на GPU
dim3 grid(GRID_SIZE);
dim3 block(BLOCK_SIZE);
time = clock();
pi_kern<<<grid, block>>>(res_d);// Запуск ядра
cudaThreadSynchronize();// Ожидаем завершения работы ядра
cudaMemcpy(res, res_d, sizeof(CUDA_FLOAT) * GRID_SIZE * BLOCK_SIZE,
cudaMemcpyDeviceToHost);// Копируем результаты на хост
cudaFree(res_d);// Освобождаем память на GPU
CUDA_FLOAT pi = 0;
for (int i=0; i < GRID_SIZE * BLOCK_SIZE; i++)
{
pi += res[i];
}
pi *= 4;
time = clock() - time;
printf("PI = %.12f\n",pi);
printf("%.4f", (double)time/CLOCKS_PER_SEC);
getch();
return 0;
}
Технический вывод программы
Расчёты проводились 10 раз. 100 000 000 слагаемых для решения числа PI, время работы программы 35~37 секунд
Расчёт на CPU
| Потоки, количество | ||||||
| Итерации | ||||||
На CPU 100 000 000 итераций занимает 598 секунд.
Приложение 1.1
Теоретическая часть
— иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим
В своей лабораторной работе я использовал два алгоритма расчета числа Пи .
Формула Леонарда Эйлера:
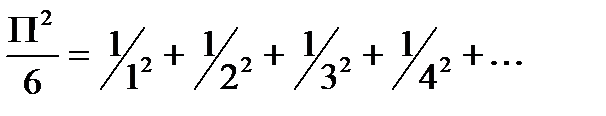
И Формулу Валлеса:
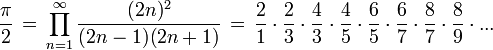
Последовательный алгоритм.
Схема 1.
Код программы представлен в приложении 1.
Параллельный алгоритм
Узким местом параллельного алгоритма является сохранение промежуточных сумм и произведений в один класс данных.
Чтобы этого избежать я сделал специальный поток в программе, который распределяет нагрузку между потоками, которые считают промежуточные суммы и произведения. А затем, после окончания расчета, отправляют данные в один глобальный класс, который защищен мьютексом, чтобы только один поток, в одно время мог записывать данные в переменную.
После поступления всех данных в общий глобальный класс, поток который распределял нагрузку между потоками, начинает считать сумму или произведение, в зависимости от алгоритма.
Такое распределение нагрузки позволило избежать постоянных задержек в ожидании записи данных.
См. схема 2, код представлен в приложении 2.
Алгоритм
Алгоритм расчёта числа PI.
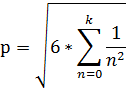
Вычислительный процессор
Intel Core i7-950
| Тактовая частота | Ядра | Кэш L2 | Кэш L3 | TDP | Разъём |
| 3.07 ГГц | 4 Ч 256 КБ | 8 МБ | 3 Ч DDR3-1066 | LGA 1366 |
Результаты эксперимента
| Потоки, количество | ||||||
| Итерации | ||||||
Таблица 1. Таблица зависимости времени выполнения, от количества итераций и потоков
| Потоки | ||||||
| Итерации | ||||||
| 1,70 | 3,00 | 2,79 | 2,79 | 2,29 | ||
| 1,87 | 3,08 | 3,08 | 3,05 | 3,01 | ||
| 1,94 | 3,27 | 3,64 | 3,20 | 3,19 | ||
| 2,01 | 3,61 | 4,30 | 4,26 | 4,11 | ||
Таблица 2. Таблица зависимости ускорения, от количества итераций и потоков
Максимальное ускорение выделено серым цветом.
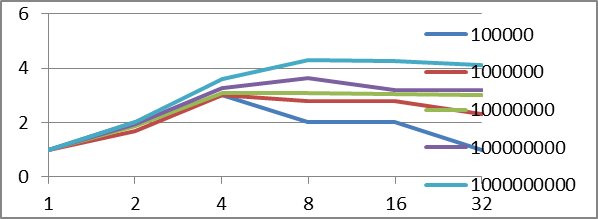
Рисунок 0. График зависимости ускорения, от количества итераций и потоков.
ПРИЛОЖЕНИЕ 1.2

Рис.1 Хронология загрузки ЦП 1 000 000 000 итераций, 1 процесс

Рис.2 Хронология загрузки ЦП 1 000 000 000 итераций, 2 процесса

Рис.3 Хронология загрузки ЦП 1 000 000 000 итераций, 4 процесса

Рис.4 Хронология загрузки ЦП 1 000 000 000 итераций, 8 процессов

Рис.5 Хронология загрузки ЦП 1 000 000 000 итераций, 16 процессов

Рис.6 Хронология загрузки ЦП 1 000 000 000 итераций, 32 процесса
ПРИЛОЖЕНИЕ 1.3
private void jButton1MouseClicked(java.awt.event.MouseEvent evt) {//GEN-FIRST:event_jButton1MouseClicked
int iter = Integer.parseInt(jTextField1.getText());
int threads = Integer.parseInt(jTextField2.getText());
Global.TimeStart();
Listner L = new Listner(iter, threads, 0);
Thread t = new Thread(L);
t.start();
try {
t.join();
} catch (InterruptedException ex) {
Logger.getLogger(multithread.class.getName()).log(Level.SEVERE, null, ex);
}
jTextArea2.insert(Double.toString(Global.F()) + "\n", 0);
Global.TimeStop();
jTextArea3.insert(Long.toString(Global.stop - Global.start) + "\n", 0);
Global.Reset();
}//GEN-LAST:event_jButton1MouseClicked
public class Listner extends Thread {
int threads, pos;
long iter;
public Listner(long iter, int threads, int pos) {
this.threads = threads;
this.iter = iter;
this.pos = pos;
}
@Override
public void run() {
long start = 1;
long delta = iter / threads;
Thread[] t = new Thread[threads];
if (pos == 0) {
First[] f = new First[threads];
for (int i = 0; i < threads; i++) {
f[i] = new First(start, start + delta);
t[i] = new Thread(f[i], "Thread " + Integer.toString(i));
t[i].start();
start = start + delta;
}
}
if (pos == 1) {
Second[] f = new Second[threads];
for (int i = 0; i < threads; i++) {
f[i] = new Second(start, start + delta);
t[i] = new Thread(f[i], "Thread " + Integer.toString(i));
t[i].start();
start = start + delta;
}
}
for (int i = 0; i < threads; i++) {
try {
t[i].join();
} catch (InterruptedException ex) {
Logger.getLogger(Listner.class.getName()).log(Level.SEVERE, null, ex);
}
}
}
}
public class First extends Thread {
long start, stop;
public First(long start, long stop) {
this.start =start;
this.stop = stop;
}
@Override
public void run() {
double summ = 0;
for (int i = (int)start; i < stop; i++) {
summ += 1 / Math.pow(i, 2);
}
Global.plus(summ);
}
}
public class Global
private static double SumF = 0, SumS = 1;
public static long start, stop;
public static synchronized void plus(double d) {
SumF += d;
}
public static synchronized void mul(double d) {
SumS *= d;
}
public static synchronized double F() {
return Math.sqrt(6 * SumF);
}
public static synchronized double S() {
return SumS * 2;
}
public static synchronized void TimeStart() {
start = System.currentTimeMillis();
}
public static synchronized void TimeStop() {
stop = System.currentTimeMillis();
}
Скриншоты программ
Инструкция пользователя
Программы имеют графический интерфейс, и различаются иконками.
Программа использующая последовательный алгоритм расчета пи имеет иконку: (onethread.exe), а параллельный :  (multithread.exe)
(multithread.exe)
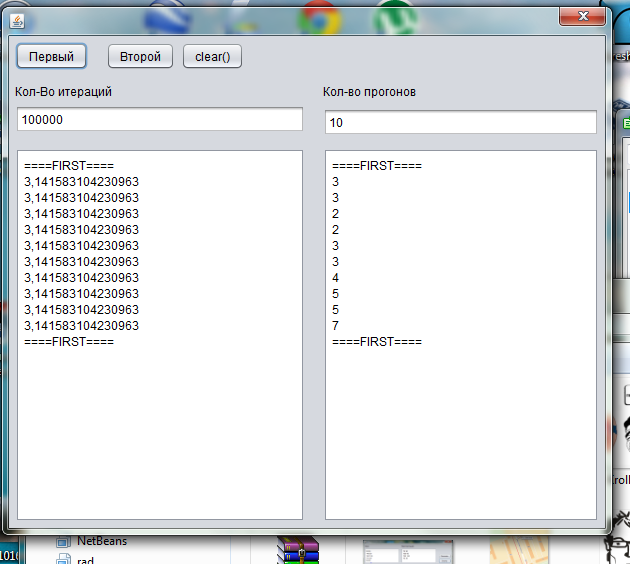
Программа onethread.exe
Программа имеет 3 кнопки
«Первый» — нажимая эту кнопку вы запускаете первый алгоритм(алгоритм Эйлера)
«Второй» — нажимая эту кнопку вы запускаете второй алгоритм (алгоритм Валлеса)
««clear()» — очистка полей
В поле «количество итераций» вводится количество итераций от 1 до 100 000 000 000
В поле «количество прогонов» вводится количество повторений алгоритма, для более точного значения.
В левом поле выводится число Пи, в правом время работы алгоритма.
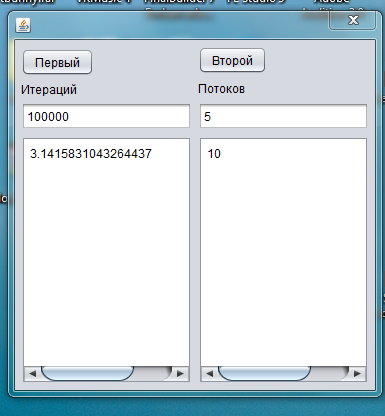
Программа multithread.exe
Программа имеет 2 кнопки
«Первый» — нажимая эту кнопку вы запускаете первый алгоритм(алгоритм Эйлера)
«Второй» — нажимая эту кнопку вы запускаете второй алгоритм (алгоритм Валлеса)
В поле «количество итераций» вводится количество итераций от 1 до 100 000 000 000
В поле «количество потоков» вводится количество повторений алгоритма, для более точного значения.
В левом поле выводится число Пи, в правом время работы алгоритма.
Бахчиванжи Дарьи
Дата добавления: 2014-12-06; просмотров: 794;
