СТРУКТУРНЫЙ СИНТЕЗ АВТОМАТА
Для выбранной синхронной модели автомата применим структурную схему, приведенную на рис.6.
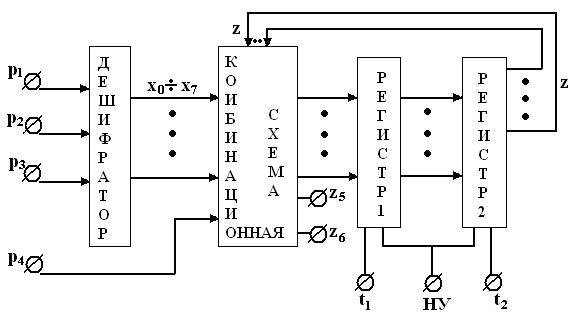
Рис. 6
Эта схема состоит из дешифратора входных сигналов, комбинационной схемы, которая реализует функции возбуждения элементов памяти и самой памяти, построенной из триггеров на двухрегистровой основе. В синхронных автоматах отсутствует необходимость бороться с функциональными и логическими состязаниями в дешифраторе и комбинационной схеме, так как предполагается, что все переходные процессы в этих схемах успевают закончиться к моменту появления первого синхросигнала t1, по которому информация с выходов комбинационной схемы записывается в триггеры регистра 1.
Триггерный регистр 2, запись информации в который осуществляется вторым синхросигналом t2, необходим для того, чтобы сделать все состояния автомата устойчивыми и исключить влияние состязаний. Триггеры регистра 1 называются вспомогательными, а триггеры регистра 2 – основными. Сигнал z5 является сигналом «Ошибка», а сигнал z6 - сигналом принадлежности входной цепочки символов языку с грамматикой G”. Сигналы Р1, Р2, Р3 – закодированные сигналы входных символов, Р4 – сигнал признака конца цепочки. Сигналом НУ (начальная установка) триггеры автомата устанавливаются в начальное состояние.
В общем случае сложность реализации автомата, точнее дешифратора и комбинационной схемы, зависит от способа кодирования входных символов. Предположим, что входные сигналы закодированы двоичным кодом, тогда входные символы x0 ÷ x7 могут быть представлены тремя кодирующими переменными 
p1, p2, и p3. В качестве символа окончания входной цепочки может быть использован любой свободный входной символ из x0 ÷ x7. Если таких нет, то необходимо ввести дополнительный, обозначив его через переменную p4.
Выделив в структурной схеме автомата дешифратор, можно упростить комбинационную схему и тем самым облегчить синтез автомата. С помощью дешифратора входные символы, закодированные двоичными переменными p1, p2, и p3, преобразуются в унитарный код, в котором только одна из переменных принимает значение 1, в то время как все другие равны нулю. Поэтому выходы дешифратора можно обозначить x0 ÷ x7. В свою очередь символ окончания входной цепочки р4 принимает значение 1 по окончании любой входной цепочки.
Пусть входные символы закодированы так, что их номера являются десятичными эквивалентами двоичных кодов (N=p1×20+ p2×21+p3×22), тогда, составив таблицу кодов (табл.1), получим, например:
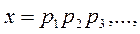
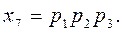
Таблица 1
| Символ | р3 | р2 | р1 |
| х0 | |||
| х1 | |||
| х2 | |||
| х3 | |||
| х4 | |||
| х5 | |||
| х6 | |||
| х7 |
Реализация дешифратора, как и всех остальных частей автомата, должна быть выполнена на логических элементах одной серии интегральных микросхем.
Выберем для реализации схемы автомата микросхемы серии КР555.
Реализация дешифратора на микросхеме данной серии приводится на рис.7.
Четыре инвертора на входе используются для снижения нагрузок на источники сигналов p1, p2, p3 и p4. Логическую функцию ЗИ – НЕ выполняют 8 логических элементов. 8 инверторов на выходе позволяют получить сигналы унитарного кода x0 ÷ x7, инверсии этих сигналов (x0 ÷ x7) получаются непосредственно с входов элементов ЗИ – НЕ.
Для реализации дешифратора в указанном виде необходимо 16 инверторов и 8 логических элементов ЗИ – НЕ.
В принципиальной схеме инверторы реализуются на микросхеме КР555ЛН1, содержащей в одном корпусе 6 инверторов, логические элементы ЗИ – НЕ на микросхеме КР555ЛА4.
Так как для работы комбинационной схемы при фиксации конца цепочки могут быть необходимы сигналы p4 и `р4, то для их формирования используются два инвертора 15, 16.
Комбинационная схема автомата реализует функцию его переходов, заданных графом переходов или таблицей переходов, с учетом выбранного варианта кодирования состояний. Все дальнейшие построения проводятся для варианта размещения, представленного на рис.5.
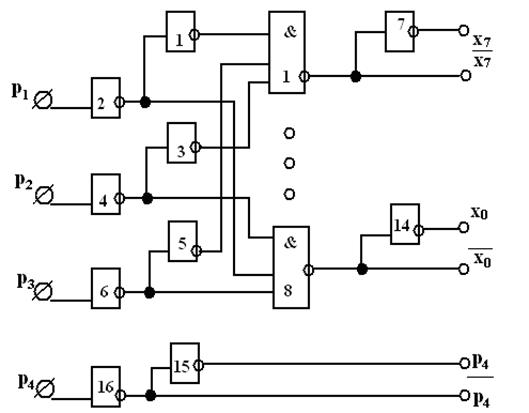
Рис. 7
Построить функцию переходов – это значит найти переключательную функцию кодирующих (внутренних) z1 ÷ z4 переменных. В соответствии со структурной схемой автомата каждая внутренняя переменная представляет состояние элемента памяти – триггера. По переключательным функциям внутренних переменных могут быть найдены функции возбуждения соответствующих им триггеров. Реализация этих функций образует комбинационную схему автомата.
Сложность функции возбуждения, а значит и сложность комбинационной схемы, в общем случае зависит от типа триггера. Известны основные три типа триггера, используемые в элементах памяти – D-триггер, RS-триггер и Т-триггер. В принципе, можно использовать любой из типов триггеров, однако мы остановим свой выбор на триггере типа D. D-триггер лишь задерживает входной сигнал, поэтому его функция возбуждения D совпадает с функцией переключения внутренней переменной zi.
Запишем функции возбуждения D-триггеров для рассматриваемого примера и результаты занесем в таблицу 2.
Таблица 2
| Символ состояния | Код состояния | Функции возбуждения | |||
| z4 z3 z2 z1 | D4 | D3 | D2 | D1 | |
| r4 |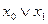 
| 
| |||
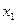
| r2 |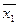 
| ||||
| r11 | |||||
| r5 |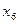 
| 
| |||
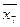
| r3 | 
| ||||
| r1 | 
|
| |||
| * | * | * | * | * | |
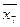
| r0 | 
|
| 
|
| |
| * | * | * | * | * | |
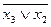
| r8 | 
| 
| |||
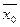
| r9 |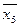 
| ||||
| r10 |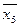
| ||||
| * | * | * | * | * | |
| r7 |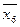 
| ||||
| * | * | * | * | * | |
| r6 |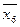
| 
|
В графе «Код состояния» таблицы представлены все возможные наборы значений внутренних переменных z1, z2, z3 и z4 в порядке возрастания их двоичных эквивалентов. В графе «Символ состояния» эти наборы помечаются условными обозначениями (r0 ÷ r11) в соответствии с выбранным вариантом размещения состояний автомата (рис. 5).
Четыре набора, которые не соответствуют никаким состояниям автомата, помечены звездочками.
Принцип составления функций возбуждения заключается в следующем.
Рассмотрим заполнение, например, строки r0 табл. 2. Из состояния r0 (код 0111) возможны три перехода: в состоянии r1 (код 0101) при поступлении на вход символа x3, в состоянии r4 (код 0000) при воздействии x2 и в состояние r6 (код 1111) при воздействии x5. В первом переходе (0111 – 0101) изменяет свое значение внутренняя переменная z2 из 1 в 0, поэтому в столбце D2 должен быть записан символ `x3. Во втором переходе (0111 – 0000) изменяют свои значения сразу три переменных z1, z2, z3, причем из 1 в 0, значит, в столбцах D1, D2, и D3 должны быть записаны символы `x2. Но так как в столбце D2 уже записан символ `x3, а изменение z2 в обоих случаях происходит из 1 в 0, то в столбце D2 должно быть записано выражение `x3`n`x2. Последнее означает, что переход из 1 в 0 переменной z2 происходит при поступлении на вход схемы символа x2 или символа x3. Наконец в третьем переходе (0111 – 1111) при поступлении символа x5 изменяется только переменная z4 из 0 в 1, поэтому в столбце D4 записывается символ x5.
Аналогично заполняются остальные строки в таблице, причем при отсутствии изменений любой из переменных z1, z2, z3, z4, в каком – либо состоянии в соответствующий столбец Di записывается значение переменой zi, определяемое данным состоянием.
Значение Di в четырех строках, отмеченных звездочками, могут быть заданы произвольно.
После задания всех функций возбуждения триггеров, представляющих собой дизъюнктивную нормальную форму (ДНФ), необходимо выполнить их минимизацию.
Для нахождения минимальной ДНФ функции возбуждения удобно воспользоваться ее геометрическим представлением на вершинах 4-мерного куба, которое для функции Д1 представлено на рис.8. На этом рисунке вершины, в которых значение функции равно 1, помечены зачерненными кружками, вершины, на которых значение функции равно 0, не имеют отметки, вершины, на которых функция не определена, помечены звездочками. Вершины, помеченные входными переменными или логическими выражениями из них, обозначаются полузачеркнутыми кружками. Этим отражается тот факт, что в этой вершине значение функции равно 1, если соответствующая переменная (или выражение) равна 1, и 0 – в противном случае. Причем инверсные и неинверсные значения переменных помечаются противоположным полузачеркиванием кружка (рис 8). При выполнении минимизации сначала выписываются импликанты (коньюкции), покрывающие зачерненные вершины (и, возможно, некоторые вершины, помеченные звездочками).
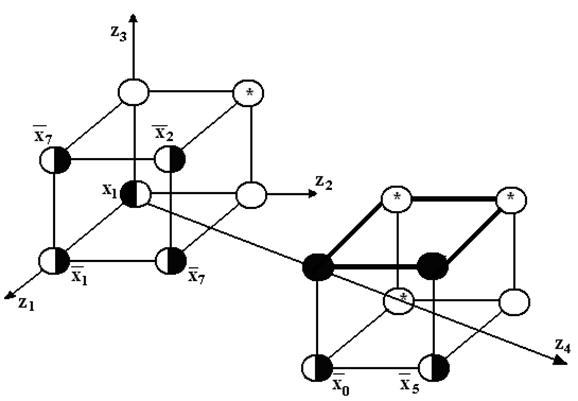
Рис. 8
После этого можно считать, что остальная часть функций задана на этих вершинах произвольно.
На рис.8 для функции D1 мы имеем две зачерненные вершины с координатами 1100 и 1110 (иначе, доопределив функцию D1) запишем импликанту, покрывающую эти вершины. Она будет иметь вид z3, z4, так как эти переменные однозначно определяют данные вершины, (переменные z3 и z4 не меняют своих значений на этих вершинах, соответственно z1 и z2 меняют значения). Выделим рассмотренное жирными линиями на рисунке.
После этого выписываются импликанты, каждая из которых накрывает одинаково отмеченные полузачеркнутые вершины и возможно большое число вершин с произвольным заданием функции или зачерненных (значение функции равно 1). Это позволяет покрыть функцию наименьшим числом импликант минимального ранга (т.е. содержащих минимальное число переменных). Начинается такая импликанта с входной переменной или логического выражения из входных переменных, соответствующих данной вершине.
Например, для вершины `x1 (координата 0001) наилучшим будет покрытие: вершина `x7 (0101), зачерненная вершина (1101) и вершина `x0 (1001). Тогда импликанта будет иметь вид: `x1. z1. `z2. `z3. `z4. В то же время, для вершины `x2 (0111) наилучшим будет покрытие с вершинами, помеченными звездочками (координаты 0110 и 1110), и зачерненной вершиной (1111), а импликанта будет иметь вид: `x2z2z3. Для вершины `x7 (0101) – вершины с координатами 0111,1111 и 1101 (две последние зачернены), а импликанта имеет вид `x7 z1`z2 z3. Здесь переменная `z2 в импликанте показывает отличие в вершине `x7 от вершины`x2. Проделав аналогичные операции для остальных вершин, получим минимальную ДНФ функции D1:
Упрощая выражение, окончательно получим минимальную ДНФ:
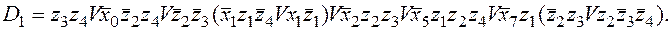
Проделаем аналогичные операции для остальных функций возбуждения.
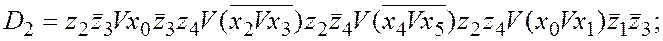
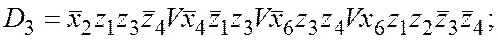
Теперь рассмотрим переключательные функции z5 и z6, представляющие выходные сигналы автомата. Сигнал z6, свидетельствующий о принадлежности цепочки входных символов языку с грамматикой G“, принимает значение 1, если автомат находится в заключительном состоянии (в нашем случае – r11) и на его вход поступает сигнал признака конца цепочки символов x8=1, в противном случае z6=0. Следовательно, z6= x8`z1 z2 `z3`z4.
Функция сигнала ошибки z5 может быть построена точно так же, как функции D1 ÷ D4, но для уменьшения сложности ее реализации можно воспользоваться следующим условием.
Сигнал ошибки вырабатывается тогда, когда при поступлении очередного входного символа внутреннее состояние автомата не изменяется (кроме случая, когда автомат находится в заключительном состоянии и на его вход подается символ признака конца цепочки). Поэтому
,
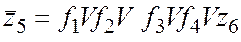где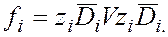 
С целью исключения возможного влияния функциональных состязаний и фиксации ошибки до момента принятия решения сигнал z5 удобно представить состоянием триггера, стробируемого синхросигналом t2. В качестве триггера, реализующего сигнал z5, может быть выбран любой тип триггера, в том числе и RS – триггер. Сигнал z6 тоже необходимо стробировать, но синхросигналом t1. При этом необязательно представлять этот сигнал состоянием триггера.
Примечание. При условии, если минимальная ДНФ функции возбуждения для прямого значения имеет высокую сложность, можно найти минимальную ДНФ для инверсии функции возбуждения и оценить ее сложность.
При этом минимальная ДНФ функции находится не инверсией выражения для прямого значения, а по ее геометрическому представлению. Для этого необходимо проинвертировать выражения, помечающие вершины с полузачеркнутыми кружками и провести минимизацию, считая, что вершины с зачеркнутыми кружками представляют нули функции, а неотмеченные вершины – единицы функции. Получив ДНФ для инверсной функции `Di, необходимо проверить ее сложность, и если она меньше сложности прямого значения Di, то использовать схему получения инверсной функции. Для получения прямого значения от инверсной функции`Di, необходимого для подачи на информационный вход, нужно проинвертировать результирующий сигнал.
Так, рассмотрим прямую и инверсную функции возбуждения для информационного входа D3. Геометрическое представление для D3. дано на рис. 9.
Функция возбуждения D3. будет иметь вид
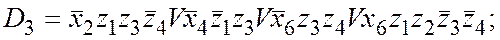
Сложность функции – 15.
Для получения функции возбуждения `D3 проинвертируем значения на помеченных вершинах, а непомеченные вершины будем рассматривать как единицы функции.
.
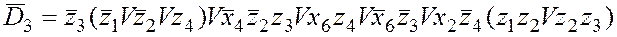Сложность функции – 17. Необходимо реализовать функцию D3.
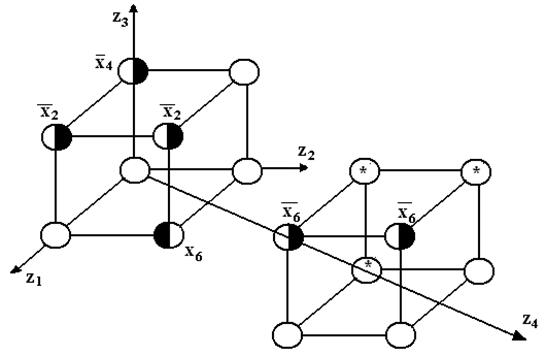
Рис. 9
Дата добавления: 2014-12-03; просмотров: 924;