Задача складання розкладу
Припустимо, що потрібно прочитати декілька лекцій у найкоротший термін. Кожна лекція окремо займає одну годину, але деякі лекції не можна читати одночасно(наприклад якщо це робить один і той самий викладач, або лекції читаються в одній і тій самій групі.) Побудувавши граф, вершини якого взаємно однозначно відповідають лекція, і дві вершини суміжності, тоді й тільки тоді, коли відповідні лекції не можна читати одночасно.
Очевидно, що будь-яке розфарбування цього графа задає можливий розклад: лекції, які відповідають вершинам одноколірного класу, читають одночасно. Навпаки, будь-який можливий розклад задає розфарбування графа. Оптимальні розклади відповідають розфарбуванням мінімальною кількістю кольорів, а час, потрібний для читання лекцій дорівнює x(G).
Задача розподілу обладнання
Задано множину V={v1,…,vn} i S={s1,…,sm} відповідно робіт і механізмів. Для виконання кожної роботи потрібен певний час, однаковий для всіх робіт, і якісь механізми. Жоден з механізмів не може бути зайнятий на декількох роботах одночасно. Потрібно розподілити механізми так, щоб загальний час виконання всіх робіт був мінімальний.
Побудувавши граф з множиною вершин, вершини якого суміжні тоді і лише тоді коли для виконання робіт потрібний хоча б один спільний механізм. Розфарбувавши граф, роботи, що відповідають вершинам одного кольору, можна виконувати одночасно, а мінімальний час виконання всіх робіт відповідає розфарбуванню мінімальною кількістю кольорів.
Задача призначення телевізійних каналів.
Передавальні станції зображають вершинами графа. Якщо відстань між будь-якими двома станціями менша за одиницю, то відповідно вершини графа з’єднуються ребром. Граф розфарбовують зіставляючи різним кольорам вершин різні канали. Мінімальна кількість каналів відповідає розфарбуванню графа мінімальною кількістю кольорів.[5]
Розділ 3
Проектування алгоритму та графічного інтерфейсу
3.1 UML-use case діаграма.
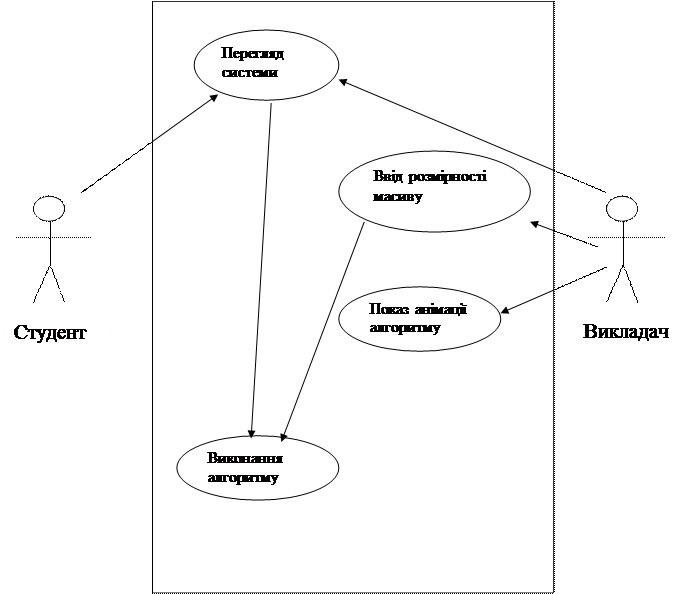
3.2 Перелік функцій системи
3.3 Функціональна схема
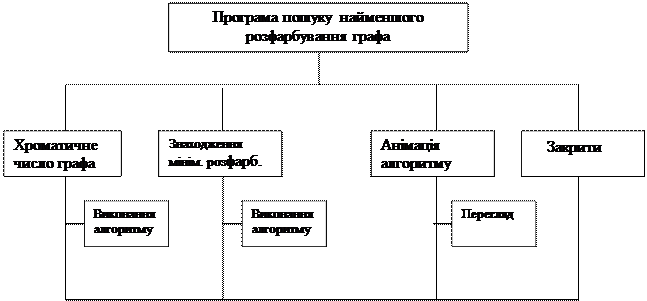 |
3.4 Проект інтерфейсу
Головне вікно
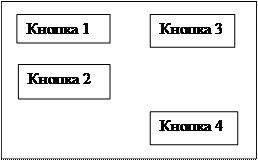
Вікно (хроматичне число графа)
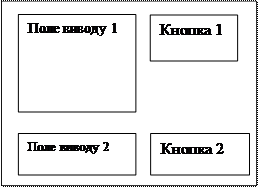
Вікно (Знаходження мінімального розфарбування)
 |
Вікно (Анімація алгоритму)
 |
Дата добавления: 2014-12-03; просмотров: 1963;
