Пример. Топологическая сортировка.
Топологической называют сортировку на множестве элементов в случае, когда на множестве элементов задано отношение частичного порядка. Порядок является частичным, если отношение предшествования задано не для всех пар элементов. Множество целых чисел является полностью упорядоченным, так как для любой пары целых чисел a,b определено отношение ‘>’ (больше) или ‘<’ (меньше).
В качестве примера ситуации, когда порядок является частичным, рассмотрим производство следующих работ:
1. сделать болт
2. сделать гайку
3. навернуть гайку на болт
Ясно, что работы 1 и 2 должны предшествовать работе 3. Запишем этот факт как 1í2 (читается: 1 предшествует 2) и 2í3. Работы 1 и 2 не связаны между собой отношением предшествования.
Другим примером, в котором имеется частичный порядок, является учебный план подготовки специалистов в ВУЗе. Курс "Основы алгоритмизации и языки программирования" должен предшествовать курсу "Структуры и алгоритмы обработки данных", но ни тот, ни другой никак не связаны с курсом "История государственного управления в России".
Третий пример: пусть требуется написать библиотеку подпрограмм, в которой некоторые из подпрограмм вызывают другие подпрограммы из той же библиотеки. Очевидно, что приступать к отладке вызывающих подпрограмм следует после завершения отладки вызываемых.
Топологическая сортировка на основе имеющегося отношения частичного порядка строит линейную последовательность элементов сортируемого множества, в которой для любой пары Xi, Xj не может быть выполнено условие Xi í Xj при i>j. Иными словами, для пары a í b, a не может появиться в выходной последовательности позже b.
Исходными данными для работы алгоритма является массив пар элементов first, second, таких, что first í second.Одна такая пара представляется структурой:
struct PAIR{
char *first;
char *second;
};
Для реализации алгоритма используются списочная структура, содержащая узлы двух типов: узлы основного списка (MAINS) и узлы подсписков (POD). Основной список двусвязный, с головой, циклический. Подсписок – односвязный, без головы и нециклический.
struct MAINS{ // cтруктура узла основного списка
int count; // счетчик числа элементов, предшествующих
//данному
char name[40]; // имя элемента
MAINS *llink; // связи двусвязного списка
MAINS *rlink;
struct POD *pod; // указатель на подсписок
};
struct POD { // структура узла подсписка
POD *next;// следующий узел подсписка
MAINS *m; // указатель на узел основного списка
};
Алгоритм имеет три фазы:
Первая фаза – первоначальное построение списочной структуры. Проходим массив пар, и для каждого элемента множества, который ещё не включен в список, создаем узел и помещаем его в хвост основного списка. Для каждой пары first, second в подсписок узла firstпомещаем узел, в поле m которого помещаем ссылку на узел основного списка second. Счетчик count узла second увеличиваем на единицу. После завершения первой фазы узел каждого элемента содержит число элементов, предшествующих данному. На рис.19 изображено состояние основного списка после завершения первой фазы для массива пар
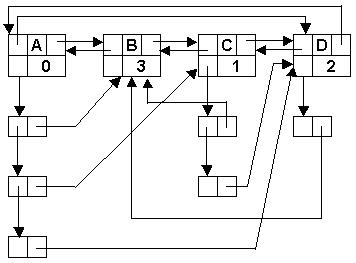 |
предшествования
Рис 19. Топологическая сортировка. 1 фаза.
Вторая фаза – создание списка ведущих элементов. Список ведущих имеет такую же структуру, что и основной список. Проходя основной список слева направо, узлы, имеющие поле счетчика, равное нулю, переносим в список ведущих элементов. Этим элементам ничто не предшествует, и они первыми будут выведены в выходную последовательность.
Третья фаза – построение выходной последовательности. Проходим список ведущих и его элементы помещаем в выходную последовательность и удаляем из списка ведущих. Проходя подсписок выводимого в результат элемента, уменьшаем на единицу поле счетчика того элемента основного списка, на который ссылается поле m подсписка. Действительно, после вывода элемента списка ведущих в результирующую последовательность, он уже не предшествует оставшимся в основном списке элементам. Если поле счетчика окажется равным нулю, переносим его в хвост списка ведущих.
Если отношение предшествования было задано корректно, то все элементы будут выведены и основной список опустеет. Если же основной список по завершении третьей фазы не пуст, то это говорит о противоречивом задании частичного порядка. Например, частичный порядок
a í b; b í c; c í a
противоречив.
Ниже приведен текст функции, реализующей топологическую сортировку:
void TopSort(PAIR *p, int n_pair, FILE *result){
// p - массив пар указателей на имена элементов
// Наличие пары s1,s2 означает,
// что s1ís2
// n_pair - число таких пар
// result - файл, в который помещаются результаты
MAINS *mhead; // голова основного списка
MAINS *vhead; // голова списка ведущих элементов
MAINS *u1,*u2,*v,*w;
Int i;
POD *x,*y;
// создание основного списка
mhead=new MAINS;
mhead->llink=mhead;
mhead->rlink=mhead;
// проход по всем парам
for(i=0; i<n_pair; i++){
// найдем или создадим элемент по имени p[i].first
u1=FindU(mhead,p[i].first);
// найдем или создадим элемент по имени p[i].second
u2=FindU(mhead,p[i].second);
// u1 предшествует u2, поэтому к счетчику u2 прибавим 1
u2->count++;
// в подсписок u1 добавим узел, указывающий на u2
x=new POD;
x->next=u1->pod;
u1->pod=x;
x->m=u2;
}
// создание списка ведущих
vhead=new MAINS; // голова
vhead->llink=vhead->rlink=vhead;
// проходим по основному списку и узлы с полем счетчика ==0
// переносим в список ведущих
for(v=mhead->rlink; v!=mhead; v=w){
w=v->rlink;
if(v->count==0){
// переносим в хвост списка ведущих
Дата добавления: 2014-12-02; просмотров: 1851;
