Aring;) .
$$ 101 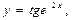
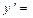 E)
E) 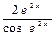 ;
;
$$$ 102 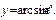
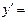 E)
E) 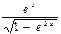 ;
;
$$$ 103 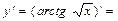
Ñ) 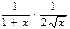 ;
;
$$$ 105 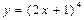 áåðiëãåí
áåðiëãåí 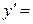
E) 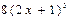
$$$ 106 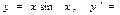
E) 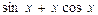
$$$ 109 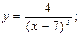
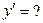 E)
E) 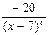 ;
;
Ocirc;óíêöèÿñûíû» êåñiíäiñiíäåãi å» ¾ëêåí ì¸íií òàáó êåðåê E) 9 .
Ocirc;óíêöèÿñûíû» êåñiíäiäåãi å» êiøi ì¸íií òàáó êåðåê. E) 7
$$$ 113 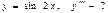 E) -
E) - 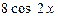
$$$ 114 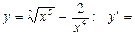 ;
;
D) 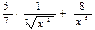 ;
;
$$$ 115 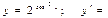
E) 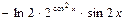 .
.
$$$ 116 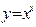 ôóíêöèÿñû áåðiëãåí.
ôóíêöèÿñû áåðiëãåí. 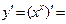
E) 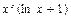 ;
;
$$$ 117 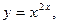
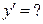 E)
E) 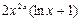
$$$ 118 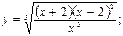
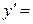
E) 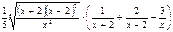
$$$167 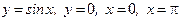 сызықтарымен шенелген жазық фигураның ауданын табыңыз: B) 2
сызықтарымен шенелген жазық фигураның ауданын табыңыз: B) 2
$$$168 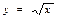
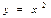 сызықтарымен шенелген фигураның ауданын табыңыз: С)
сызықтарымен шенелген фигураның ауданын табыңыз: С) 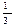
$$$ 211 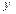 және
және 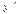 айнымалдарына қатысты сызықтық дифференциалдық теңдеуді көрсетіңіз
айнымалдарына қатысты сызықтық дифференциалдық теңдеуді көрсетіңіз
A) 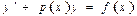
$$$ 220 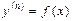 - дифференциалдық теңдеуінің жалпы шешімін табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз E)
- дифференциалдық теңдеуінің жалпы шешімін табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз E) 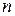 -рет тікелей интегралдау
-рет тікелей интегралдау
Z
$$191 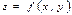 функциясының
функциясының 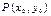 нүктесіндегі x бойынша дербес өсімшесін көрсетіңіз
нүктесіндегі x бойынша дербес өсімшесін көрсетіңіз
А) 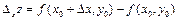
$$$192 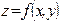 функциясының
функциясының 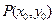 нүктесіндегі y бойынша дербес өсімшесін көрсетіңіз
нүктесіндегі y бойынша дербес өсімшесін көрсетіңіз
В) 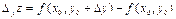
$$$193 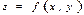 функциясының
функциясының 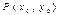 нүктесіндегі толық өсімшесін көрсетіңіз
нүктесіндегі толық өсімшесін көрсетіңіз
С) 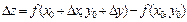
$$$194 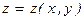 функциясының
функциясының 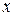 айнымал бойынша дербес туындысы:
айнымал бойынша дербес туындысы:
D) 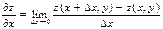
$$$195 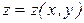 функциясының y айнымал бойынша дербес туындысы:
функциясының y айнымал бойынша дербес туындысы:
Е) 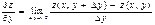
$$$196 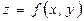 функциясының
функциясының 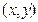 нүктесіндегі дифференциалын көрсетіңіз
нүктесіндегі дифференциалын көрсетіңіз
А) 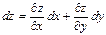
$$$197 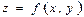 функциясының
функциясының 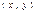 нүктесіндегі екінші ретті дифференциалын көрсетіңіз
нүктесіндегі екінші ретті дифференциалын көрсетіңіз
В) 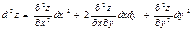
$$$201 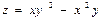 функциясының толық дифференциалын табыңыз:
функциясының толық дифференциалын табыңыз:
А ) 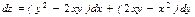
U
$$$131 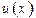 ,
, 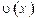 дифференциалданатын функциялары үшін, бөліктеп интегралдау формуласын жазу керек:
дифференциалданатын функциялары үшін, бөліктеп интегралдау формуласын жазу керек: 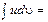 А)
А) 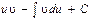
F
$$$147 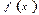 функциясының
функциясының 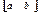 кесіндісіндегі анықталған интегралы келесі шек түрінде анықталады:
кесіндісіндегі анықталған интегралы келесі шек түрінде анықталады: 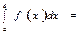
B) 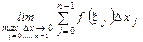
$$$ 221 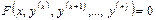 теңдеуінің жалпы интегралын табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз
теңдеуінің жалпы интегралын табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз
А) 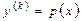
$$$ 222 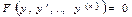 теңдеуінің жалпы интегралын табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз
теңдеуінің жалпы интегралын табуға арналған әдісті немесе айнымал ауыстыруын көрсетіңіз
В) 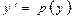
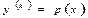
G
$$$ 306 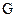 беті
беті 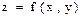 ,
, 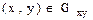 теңдеуімен берілген.
теңдеуімен берілген. 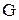 бетінің ауданын табу керек.
бетінің ауданын табу керек.
A) 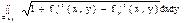
Lim
$$$ 35 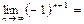 E) шек жоқ
E) шек жоқ
$$$ 37 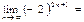 B) -∞
B) -∞
$$$ 38 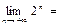 C) +∞
C) +∞
$$$ 39 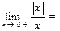 D) 1
D) 1
$$$ 40 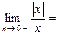 E) -1
E) -1
$$$ 41 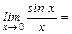 A) 1
A) 1
$$$ 42 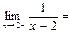 B) -∞
B) -∞
$$$ 43 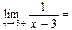 C) +∞
C) +∞
$$$49 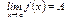 шегі бар болуы үшін келесі шарттың: D)
шегі бар болуы үшін келесі шарттың: D) 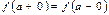
орындалуы, қажетті және жеткілікті
$$$ 62 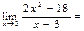 В)12 ;
В)12 ;
$$$ 63 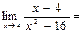 C)
C) 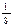
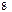 ;
;
$$$ 64 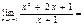 D) 0;
D) 0;
$$$ 65 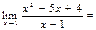 Е) е–3;
Е) е–3;
$$$ 66 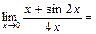 À)
À) 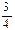 ;
;
$$$ 67 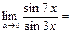 В)
В) 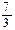 ;
;
$$$ 68 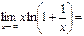 С) 1;
С) 1;
$$$ 69 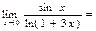 D)
D) 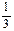 ;
;
Дата добавления: 2014-12-02; просмотров: 1279;
