и 10 (пониженной точности) Ra≤2,5 Rz≤40.
(чертежи поэтажных планов, фасадов, разрезов, генеральных планов и строительных элементов)
И 5 (особо точные) Ra≤0,63.
Применяются: в выходных звеньях ответственных кинематических цепей счетно-решающих, отсчетных и других особо точных механизмов и устройств; в высокоточных механизмах при окружных скоростях зубьев от 15 до 35 м/с прямозубых и от 30 до 70 косозубых колес.
Высокоточная) Ra≤0,63.
В кинематических цепях счетно-решающих, отсчетных, делительных, измерительных и других высокоточных механизмов. Передачи, работающие при окружных скоростях зубьев до 15 м/с прямозубых и до 30 м/с косозубых колес.
Точная) Ra≤1,25.
В системах управления и регулирования, в точных приборах. Передачи, работающие при окружных скоростях зубьев до 10 м/с и умеренных нагрузках.
Средней точности) Ra≤2,5.
Неответственные кинематические цепи приборов управления и регулирования, приборы средней точности. Передачи общего машиностроения, не требующие особой точности и работающие при окружных скоростях до 6м/с.
и 10 (пониженной точности) Ra≤2,5 Rz≤40.
Передачи, к которым не предъявляются требования точности, работающие при окружных скоростях зубьев до 2 м/с.
Рекомендации по выбору вида сопряжения зубчатых механизмов
H – применяются для тихоходных ступеней счетно-решающих, отсчетных и других точных механизмов и следящих систем при однородных материалах корпуса и колес.
G – для таких же механизмов при средних числах оборотов колес, а также при небольших колебаниях температуры, когда материалы корпуса и колес имеют разные коэффициенты линейного расширения 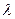 .
.
F – для быстроходных ступеней отсчетных, счетно-решающих и других точных механизмов следящих систем, приборов и силовых редукторов при средней и большой частоте вращения колес и значительных колебаниях температуры колес и корпуса, изготовленных из материалов с разным 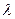 .
.
E и D – для механизмов при пониженных требованиях к точности, средней частоте вращения колес, больших колебаниях температуры колес и корпуса имеют разные 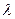 .
.
Вид сопряжения H относится к 4…7 степеням точности, G→4…8; F, E и D→4…10.
Параметры передач с эвольвентным профилем зубьев колес
Основные требования, предъявленные к зубчатой передаче можно разделить на следующие три группы:
Кинематические – обеспечение постоянства заданного передаточного числа как в процессе зацепления каждой пары зубьев, так и за любой период работы передачи.
Эксплуатационные – малые скорости скольжения и износ зубьев, высокий к.п.д. передачи, точности, компактность, плавность работы и малый шум.
Технологические – простота изготовления колес высокопроизводительными способами, возможность нарезания одним инструментом прямозубых и косозубых колес с разным числом зубьев.
Требования, предъявленным к зубчатым передачам, наиболее полно удовлетворяет эвольвентное зацепление, поэтому оно стандартизировано и получило преимущественное применение в механизмах различного назначения.
Эвольвентной, или разверткой окружности, называется кривая, которую описывает любая точка прямой линии, перекатываемой без скольжения по окружности радиуса 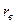 . Эта прямая называется производящей прямой, а окружность, представляющая собой геометрическое место центров кривизны эвольвенты, называется основной окружностью или эволютой.
. Эта прямая называется производящей прямой, а окружность, представляющая собой геометрическое место центров кривизны эвольвенты, называется основной окружностью или эволютой.
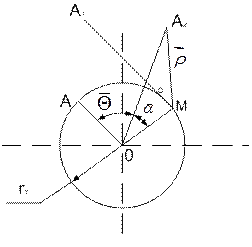
Из способа образования эвольвенты следует, что MA=MA2. Форма эвольвенты зависит от 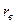 . Из треугольника OMA2 находим радиус вектор точки А эвольвенты r=OA2 =
. Из треугольника OMA2 находим радиус вектор точки А эвольвенты r=OA2 = 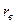 /cos
/cos 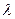 и радиус кривизны эвольвенты
и радиус кривизны эвольвенты 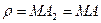 или
или 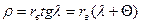 . Отсюда определяем молярный угол наклона радиус-вектора
. Отсюда определяем молярный угол наклона радиус-вектора 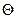 (град), который представляет собой эвольвентную функции и называется инволютой
(град), который представляет собой эвольвентную функции и называется инволютой 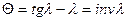 . Значения
. Значения  приводятся в таблицах и используются при расчетах размеров зубьев колес.
приводятся в таблицах и используются при расчетах размеров зубьев колес.

Меньшее зубчатое колесо называют шестерней(z1), а большее колесом(z2); термин «зубчатое колесо» является более общим.
Зацепление двух зубчатых колес z1 и z2 с кинематической точки зрения можно представить как качение без скольжения двух окружностей диаметром d1 и d2, называемых начальными.
Здесь уместно обратить внимание на различие понятий начальных и делительных окружностей колес. Делительная окружность – понятие, свойственное отдельному колесу. Диаметр делительной окружности равен произведению числа зубьев колеса z на стандартный модуль m: d=mz и не зависит от делительного межосевого расстояния a=0,5(d2±d1)=0,5m(z2±z1). Начальные окружности – центроиды относительного движения колес – понятие кинематическое и относится к колесам, находящимся в зацеплении.
Основные размеры колес пропорциональны модулю зацепления. Модуль m является основной характеристикой зацепления. Модулем называется часть делительного диаметра колеса приходящаяся на один зуб m=d/z=t/∏ где t – шаг зубчатого колеса.
Величина модуля предварительно определяется по конструктивным соображениям или расчетом зубьев на прочность и отношение устанавливается в соответствии с ГОСТ 9563-60
1 ряд 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25.
2 ряд 0,055; 0,7; 0,9; 0,11; 0,14; 0,18; 0,22; 0,28; 0,35; 0,45; 0,55; 0,7…
Зубчатые колеса с модулем m≤1 называются мелкомодульными.
Передаточное число для пары зубчатых колес будет равно: 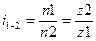 где n1 и n2 – числа оборотов зубчатых колес.
где n1 и n2 – числа оборотов зубчатых колес.
Параметры цилиндрических колес
Размеры элементов колеса для цилиндрических колес применяются следующие:
А) шаг по делительной окружности t=П*m;
Б) высота головки зуба h’=f0*m, где f0 коэффициент высоты головки зуба.
В) высота ножки зуба h”=( f0+C0)m, где C0 коэффициент радиального зазора.
Г) диаметр делительной начальной окружности.
Д) диаметр окружности высоты зубьев
Е) диаметр окружности впадин зубьев.
Ж) длина зуба B определяется как произведение межосевого расстояния А на соответствующий коэффициент длины зуба 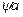 , где
, где 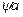 принимается равным:
принимается равным:
0,01…0,1 – для кинематических и слабонагруженных передач.
0,1…0,3 – для легконагруженных передач.
0,3…0,5 – для средненагруженных передач.
Материал колес
Выбор материала колес производится с учетом необходимой износостойкости слоев зубьев (против выкрашивания, абразивного износа и задания) и прочности их на изгиб(излом).
Наиболее часто колеса изготовляются из качественных конструкционных сталей марок 35, 40, 45, 50 и 50Г и легированных сталей 40Х, 45ХН.
При средних нагрузках для уменьшения влияния термообработки на прочность колес зубья нарезаются после улучшения или нормализации заготовок (твердость НВ≤320…350).
При больших нагрузках для повышения прочности зубчатых колес зубья подвергают объемной или поверхностной закалке (твердость НВ>350) и последующей чистовой обработке – шлифованию и притирке.
Для повышения стойкости зубьев против заедания рекомендуется применять разные материалы для колеса и шестерни. Так как последняя делает больше оборотов, то ее зубья должны быть тверже.
Для колес , работающих при нагрузке с толчками, применяются малоуглеродистые стали марок 15Х и 20Х, реже 15 и 20. После цементации (насыщения углеродом) и закалки достигается твердость поверхностных слоев зубьев НРС 56…63.
Для уменьшения потерь на трение и увеличения к.п.д. в приборах применяются колеса из бронзы Бр0Ф10-1,БрАЖ9-4,БрАМЦ9-2, работающие в паре со стальными колесами.
Для уменьшения шума и вибраций зубчатые колеса выполняют из текстолита, капрона, нейлона и других полиамидов, которые работают в паре с металлическими колесами.
Расчет передачи
Передачи прямозубыми цилиндрическими колесами при окружной скорости V<6 м/с, редко до 10, к.п.д. 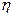 =0,98…0,92. Наименьшее число зубьев нормальных колес zmin≥17.
=0,98…0,92. Наименьшее число зубьев нормальных колес zmin≥17.
Исходными данными являются: частота вращения валов 1 и 2 n1 и n2(об/мин), передаточное отношение i12=n1/n2 и крутящий момент(нагрузка) на ведомом валу µ2, Н*м.
При конструировании зубчатых передач приборов в процессе разработки кинематической компоновочной схемы механизма обычно задаются модулем m, числами зубьев z1 и z2, диаметрами делительных окружностей d1 и d2, можосевым расстоянием A, длиной зубьев B, материалами колес и допускаемыми напряжениями. Целью расчета в этом случае является проверка условий износостойкости зубьев 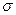 к≤[
к≤[ 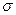 ]к и прочности зубьев на изгиб. При конструировании силовых механизмов, если размерами колес заранее не задаются, целью расчета является определение размеров колес по выбранным материалам и соответствующим им значениям.
]к и прочности зубьев на изгиб. При конструировании силовых механизмов, если размерами колес заранее не задаются, целью расчета является определение размеров колес по выбранным материалам и соответствующим им значениям.
Силы, действующие на зубья колес
Если не учитывать силы трения, то действующие на зубья силы N будут направлены по общей нормали к профилям зубьев колес 1 и 2 в зоне их контакта. Нормальные силы N можно разложить на составляющие: окружные P и радиальные Q. Величина этих сил зависит от приложенного к валу момента µ2. зависимость между этими силами:
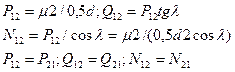
Эти силы учитывают при расчете зубьев колес, валов и подшипников механизма.
Наибольшие нормальные силы действуют на зубья колес, когда в зацеплении находится одна пара зубьев, при этом зона их контакта находится около полюса зацепления. Поэтому усталостное разрушение зубьев происходит в средней части боковой поверхности зуба. Неточности изготовления и сборки передачи, упругие деформации валов и колес, толчки и удары, происходящие в момент входа зубьев в зацепление, учитывают путем введения в расчетные формулы коэффициента концентрации нагрузки Кк и коэффициента динамичности нагрузки Кд.
Расчетную удельную нагрузку q (Н/м)при длине полоски контакта зубьев B определяют по формуле:
q=N*Kk*Kд/B.
Коэффициент концентрации нагрузки определяется отношением наибольшей удельной нагрузки к ее средней величине Кк=qmax/q. Принимают Кк=1 при расположении колес посередине между подшипниками, при коротких и жестких валах и при колесах, изготовленных из пластмасс, бронзы или стали, если твердость поверхности зубьев НВ<350, так как упругая податливость и быстрая приработка зубьев уменьшают неравномерность распределения нагрузки по длине зуба. Ориентированные значения Кк=1,1…1,3. При этом Кк соответственно увеличиваются с увеличением 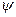 =В/А от 0,4 до 1. Кк тем больше, чем меньше жесткость валов, тверже материал зубьев (НВ>350), ниже степень точности колес относительно подшипников.
=В/А от 0,4 до 1. Кк тем больше, чем меньше жесткость валов, тверже материал зубьев (НВ>350), ниже степень точности колес относительно подшипников.
Коэффициент динамичности нагрузки определяется отношением полной нагрузки к нормальной силе Кд=(N+Nд)/N. Величина динамической нагрузки Nд тем больше, чем ниже степень точности колес, выше окружная скорость зубьев и больше массы звеньев, связанных с валами передачи.
Расчет зубьев на контактную прочность
Опытами установлено, что усталостное разрушение поверхности зубьев происходит в средней по высоте зуба зоне. Целью расчета является определение размеров колес, при которых расчетные контактные напряжения в материале зубьев не превышающей допустимой величины 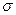 к.
к.
В качестве теоретической основы расчета зубьев используется формула Герца, выражающая результаты исследования напряжений (МПа) в зоне контакта примятых друг к другу по образующим двух стальных цилиндров, 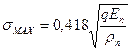 где q – удельная нагрузка на 1 мм длины полоски контакта цилиндров, Н/м; En – приведенный модуль упругости материалов цилиндров, МПа;
где q – удельная нагрузка на 1 мм длины полоски контакта цилиндров, Н/м; En – приведенный модуль упругости материалов цилиндров, МПа; 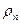 - приведенный радиус кривизны цилиндров, мм.
- приведенный радиус кривизны цилиндров, мм.
Выразим q и 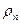 через параметры зубчатой передачи:
через параметры зубчатой передачи:
А=r2±r1=r1(i12±1); r1=A(i12±1); r2=Ai12(i12±1)
Где r1=0,5d1 и r2=0,5d2. Знак плюс относится к передачам внешнего зацепления, а знак минус – внутреннего зацепления. Радиусы кривизны эвольвент при контакте зубьев в полюсе зацепления:
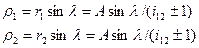
Приведенный модуль упругости при разных материалах зубьев 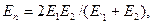 значения E1 и Е2 – из таблиц.
значения E1 и Е2 – из таблиц.
Нормальная сила 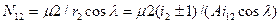
Расчетная удельная нагрузка на зуб 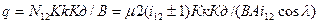
Подставляя приведенные значения q En и 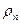 , получим формулу для определения константного напряжения снятия
, получим формулу для определения константного напряжения снятия
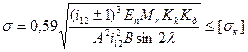
Задаваясь отношением 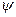 и значением [
и значением [ 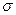 ]к, можно определить расчетное межосевое расстояние.
]к, можно определить расчетное межосевое расстояние.
Расчет зубьев на изгиб
Целью расчета является предотвращение излома зубьев. Расчетные напряжения изгиба в зубьях 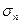 не должны превышать допускаемых [
не должны превышать допускаемых [ 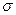 ]n/.
]n/.
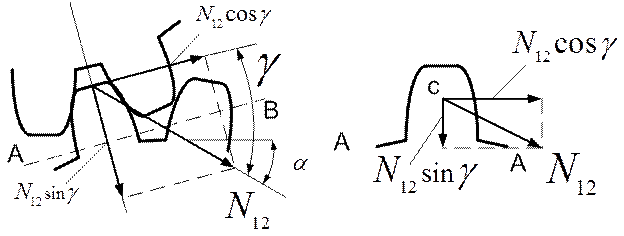
Расчет зуба на изгиб ведется на основе предположения, что в зацеплении находится одна пара зубьев. Наибольшее напряжение изгиба возникают у основания зуба, когда нормальная сила N12 приложена к вершине зуба и создает наибольший изгибающий момент. Перенесем точку приложения N12 на ось симметрии зуба и разложим на составляющие: 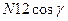 -изгибающую зуб и
-изгибающую зуб и 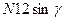 - сгибающую зуб. Из рисунка видно, что зуб работает на изгиб и сжатие, как консольная балка прямоугольного сечения. Описанное сечение АВ определяется графически вписыванием в профиль зуба параболы с вершиной в точке C, очерчивающей балку равного сопротивления изгибу (
- сгибающую зуб. Из рисунка видно, что зуб работает на изгиб и сжатие, как консольная балка прямоугольного сечения. Описанное сечение АВ определяется графически вписыванием в профиль зуба параболы с вершиной в точке C, очерчивающей балку равного сопротивления изгибу ( 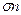 =const в любом сечении балки). В точках В и А, в которых парабола касается профиля зуба, возникают наибольшие напряжения изгиба.
=const в любом сечении балки). В точках В и А, в которых парабола касается профиля зуба, возникают наибольшие напряжения изгиба.
Опыты показали, что в зоне А на растянутой стороне зуба по действием напряжений изгиба, изменяющихся по пульсирующему циклу, появляются усталостные трещины, т.е начинается разрушение зуба. Поэтому проверка прочности зубьев производится по суммарным напряжениям на растянутой стороне зуба
где l – плечо действия изгибающей силы мм;
W – момент сопротивления опасного сечения зуба;
B и S – длина и толщина зуба, мм.
Подставляя эти значения в (1) и уменьшая числитель и знаменатель правой части на m, находим:
Заменяем в этой формуле выражение в скобках на 1/у, подставляем в нее Т12=м2/r2*cosα=м2(i12±1)/Ai12cosα, вводим коэффициенты Кк и Кд и получаем формулу для определения расчетных напряжений изгибав опсном сечении зуба(МПа)
Задаваясь коэффициентом 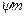 и
и 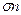 можно вычислить модуль:
можно вычислить модуль:
Принимают ближайшее большее значение m по ГОСТ и уточняют размеры колес по вышеприведенным формулам.
Для приборных механизмов и коробок скоростей применяют 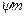 =5…12, а для редукторов малой и средней мощности
=5…12, а для редукторов малой и средней мощности 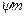 =10…30
=10…30
Величину у называют коэффициентом формы зуба и выбирают по имеющимся таблицам в зависимости от числа зубьев z.
Передачи косозубыми цилиндрическими колесами
Они работают более плавно и с меньшим шумом, чем передачи прямозубыми колесами. Они применяются при V=3…30 м/с, i12=0,2…6, к.п.д.=0,98…0,92. у косозубых колес зубья расположены по углом наклона 7…15° к образующей делительного цилиндра. Колеса, находящиеся в зацеплении, имеют одинаковые углы 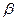 , но разное (правое и левое) направления винтовых линий.
, но разное (правое и левое) направления винтовых линий.
Передачи коническими зубчатыми колесами
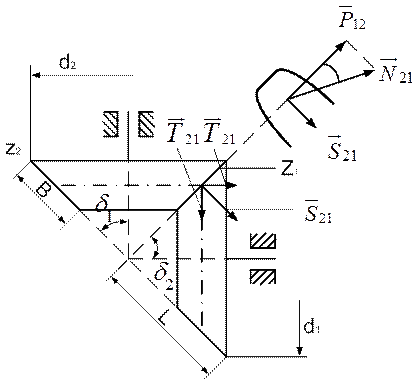
Применяют при пересекающихся осях валов. Обычно межосевой угол 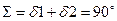 , передаточное отношение i12=n1/n2=z2/z1=d2/d1=0,3…5. В силовых передачах к.п.д.=0,98…0,92, а в приборных чем меньше нагрузки, тем ниже к.п.д. При V<3 м/с используют прямозубые колеса с косыми криволинейными зубьями. По мере приближения к вершине конуса размеры сечения и шаг зубьев уменьшаются.
, передаточное отношение i12=n1/n2=z2/z1=d2/d1=0,3…5. В силовых передачах к.п.д.=0,98…0,92, а в приборных чем меньше нагрузки, тем ниже к.п.д. При V<3 м/с используют прямозубые колеса с косыми криволинейными зубьями. По мере приближения к вершине конуса размеры сечения и шаг зубьев уменьшаются.
Эти передачи сложнее цилиндрических в изготовлении и монтаже, т.к. требуют специальных и более сложных станков и инструмента. Кроме допусков на линейные размеры, здесь требуется выдерживать допуск на межосевой угол 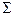 и на углы наклона образующих начальных конусов
и на углы наклона образующих начальных конусов 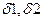 , а при монтаже совпадение вершин конусов.
, а при монтаже совпадение вершин конусов.
Размеры конического зубчатого колеса характеризуются в сечении по большому торцу модулем m, который берется по ГОСТ; диаметр делительной окружности dd=mz, а средний модуль mcp=m(1-0,5 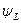 )/. Величина
)/. Величина 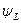 =B/L≤0,3 и берется в зависимости от степени точности величины представляемых нагрузок.
=B/L≤0,3 и берется в зависимости от степени точности величины представляемых нагрузок.
Силы, действующие в зацеплении
Нормальную силу N12, приложенную в средней точке полости контакта зубьев, разложим на составляющие: окружную P12 и радиальную S12. Затем силу S12, действующую вдоль образующих средних дополнительных конусов, разложим на радиальную Q12 и осевую T12 для конического колеса z. Все силы выразим через окружную силу P12, которую легко найти по заданному крутящему моменту(нагрузке) 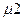 на ведомо валу:
на ведомо валу:
Действие этих сил учитывают при расчете зубьев колес, валов и подшипников механизма.
Реечная передача
Служит для преобразования вращательного движения в поступательное и наоборот; применяется в силовых механизмах редко, в основном в механизмах настройки. Основной характеристикой передачи является модуль m=t/П. деталями реечной передачи являются зубчатое колесо и рейка; зубья рейки могут нарезаться как непосредственно на детали, так и на отдельной заготовке плоской формы.
Червячные передачи
Применяются в приборах и машинах различного назначения при перекрещивающихся осях ведущего 1 и ведомого 2 валов, когда требуется осуществить передаточное отношение i12=7…100 и более.
В осевом сечении витки червяка имеют форму зубчатой рейки со стандартным модулем m, которая находится в зацеплении с зубчатым колесом. Для нормальной работы передачи необходимо, чтобы осевой шаг червяка и окружной шаг колеса были равными p=П*m.
В червячной передаче ведущим звеном обычно является червяк, число заходов которого принимают z1=1…4. Число зубьев колеса следует принимать z2>26, так как при z2<26 происходит подрезание ножки зуба головкой зуба инструмента.
Передаточное отношение червячной передачи червяка 1 к колесу 2 при угле подъема витка червяка 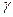 :
:
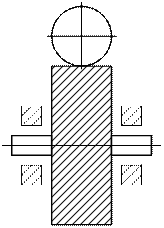
Наибольшее распространение получили червячные передачи, у которых зубья колеса имеют вогнутую форму и охватывают червяк (как гайка винт) по дуге с углом охвата 2 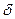 =60…110°. При этом получается линейный контакт между зубьями колеса и витками червяка. Такие передачи обладают высокой нагрузочной способностью.
=60…110°. При этом получается линейный контакт между зубьями колеса и витками червяка. Такие передачи обладают высокой нагрузочной способностью.
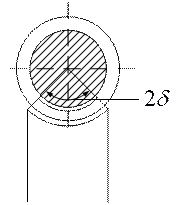
Передачи с ведущим колесом применяются редко в некоторых приборах при 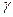 >15° и z1≥4.
>15° и z1≥4.
Достоинствами червячной передачи являются: контактность – малые габариты при больших передаточных числах; плавность и бесшумность работы; надежность и простота в эксплуатации; возможность самоторможения.
Недостатками червячной передачи являются: низкий к.п.д.=0,5…0,8; необходимость применения высококачественных бронз для зубьев колеса с целью уменьшения 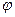 ; высокая стоимость инструмента для нарезания зубьев колес; высокие требования к точности изготовления и сборки.
; высокая стоимость инструмента для нарезания зубьев колес; высокие требования к точности изготовления и сборки.
Геометрические размеры
В червячной передаче применяются червяки трех типов: архимедовы, коволютные и эвольвентные.
Архимедовы червяки в осевом сечении имеют прямолинейный трапециидальный профиль, а в торцевом – профиль, очерченный по архимедовой спирали. Эти червяки применяются наиболее часто.
Конволютные червяки в осевом сечении имеют выпуклый профиль, а в нормальном сечении витка – прямолинейный трапециидальный.
Эвольвентные червяки в осевом сечении имеют выпуклый эвольвентный профиль косозубых колес с малым z и большим 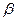 .
.
Профиль зубьев колес определяется инструментом, который должен соответствовать форме и размерам червяка.
Стандартным модулем червячной передачи считается осевой модуль червяка m, равный торцовому модулю колеса. Угол профиля червяка в осевом сечении 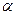 =20°.
=20°.
Основные размеры червяка и червячного колеса
1. число зубьев колеса z2=z1*i12.
2. расчетный шаг червяка(колеса) p=m*П.
3. ход витка червяка pz=z1*p.
4. коэффициент диаметра червяка q=d1/m
5. угол подъема линии витка червяка 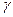 =arctg(z1/q)
=arctg(z1/q)
6. делительный диаметр червяка(колеса) d1=q*m d2=z2*m
7. высота делительной головки витка червяка (зуба колеса) ha=m
8. высота делительной ножки витка червяка (зуба колеса) hf=1,25m.
9. диаметр вершин витков червяка (колеса) df1=d1-2hf; da2=d2-2hf.
10. диаметр впадин червяка (колеса) df1=d1-2hf; df2=d2-2hf;
11. ширина венца червячного колеса (по впадинам зуюбев) B≈da*2П*2 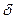 /360°.
/360°.
12. длина нарезанной части червяка B1≥2m( 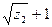 )
)
13. делительное межосевое расстояние A=0,5(d1+d2)=0,5m(q+z2)
Значение 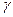 определяется по таблицам в зависимости от m, q и z1.
определяется по таблицам в зависимости от m, q и z1.
Для мелкомодульных передач значения q принимаются больше с целью увеличения жесткости червяка. Для силовых передач рекомендуется выбирать z2=26…80, так как при z2<26 ухудшаются условия работы зубьев, а при z2>80 получаются большие габариты передачи.
Конструкция и материалы колес и червяков
Червяки обычно выполняются за одно целое с валом. Материалом для них служат стали. Червяки из стали 40, 45, 40Х и 40ХН закаливают до твердости HRC 45-60. червяки из стали 15, 20, 15Х, 10Х, 20ХФ цементируют и закаливают до твердости YRC 56-62. Незакаленные червяки с твердостью поверхности НВ<270 применяются в ручных или тихоходных маломощных передачах.
Червячные колеса чаще делают составными: венец из бронзы, а колесо из стали или чугуна. Венец насаживается на колесо с горячей или прессовой посадкой и закрепляются стопорными винтами dв=(1,2..1,5)m и длиной lв=(0,3…0,4)В и цилиндрическими шпонками-штифтами lмм=lв. При малой толщине и большом диаметра диска применяется фланцевое применение. Цельные колеса из чугуна С415-32 и С421-40 применяются в передачах при скорости Vs<2 м/с.
Лучшим антифрикционным материалом для зубьев колеса являются бронзы БрОФ10-1, БрОНФ. Они применяются для ответственных передач при V>3 м/с. Безоловянистые бронзы БрАЖ9-4 и БрАЖН10-4-4 хуже сопротивляются заеданию при V>6 м/с.
Силы, действующие в зацеплении
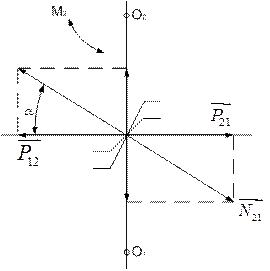
Предположим, что к валу колеса приложен крутящий момент 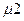 . Будем считать, что нормальная сила N приложена в полюсе зацепления. Разложим силу N таким образом , чтобы получить взаимно перпендикулярные силы: окружные P12 и P21, радиальные Q12 и Q21 и осевые T12 и Т21. При этом следует учесть, что под действием силы трения сила S отклоняется на угол трения
. Будем считать, что нормальная сила N приложена в полюсе зацепления. Разложим силу N таким образом , чтобы получить взаимно перпендикулярные силы: окружные P12 и P21, радиальные Q12 и Q21 и осевые T12 и Т21. При этом следует учесть, что под действием силы трения сила S отклоняется на угол трения 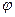 от плоскости действия силы N.
от плоскости действия силы N.

Для передачи со стальным червяком и бронзовыми зубьями колеса принимают следующие значения 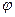 в зависимости от скорости скольжения Vs=0,5d1*w1/cos
в зависимости от скорости скольжения Vs=0,5d1*w1/cos 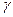 (
( 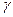 - угол подъема витка червяка):
- угол подъема витка червяка):
Vc м/с 0,01…0,1 0,1…0,5 0,5…2,5 2,5…10
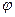 ° 7…5 5…3 3…2 2…1
° 7…5 5…3 3…2 2…1
Определяем окружную силу на колесе P12,равную осевой силе на червяке Т21 при известном 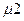 :
:
P12=T21=2 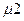 /d2
/d2
Радиальные силы на колесе Q12 и червякеQ21 равны между собой, но направлены в противоположные стороны
Q12=P12tgα=Q21
Осевая сила на колесе Т12 равна окружной силе на червяке P21, но направлена в противоположную сторону
Т12=Р21=Р12tg( 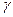 +
+ 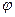 )=2
)=2 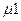 /d1
/d1
Где 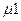 -крутящий момент на валу червяка.
-крутящий момент на валу червяка.
Учитывая, что угол наклона зубьев на колесе 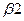 равен углу подъема винтовой линии червяка
равен углу подъема винтовой линии червяка 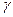 при cos(αn)≈cos(α) и cos(
при cos(αn)≈cos(α) и cos( 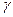 +
+ 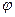 )≈cos(
)≈cos( 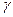 ). Находим нормальную силу N12=P12/(cos(
). Находим нормальную силу N12=P12/(cos( 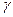 +
+ 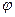 )cos(αn))=2
)cos(αn))=2 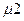 /( α2*cos(
/( α2*cos( 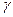 )*cos(α))
)*cos(α))
Сила N12 учитывается при расчете зубьев колеса на прочность.
Расчеты на прочность
Расчеты червячных передач на прочность основаны на тех же принципах, что и расчеты зубчатых передач. При этом рассчитываются зубья колес, так как витки стального червяка всегда более прочные.
При расчете зубьев колеса на прочность учитывается следующее:
1. Бронзовые зубья колеса в процессе эксплуатации прирабатываются к виткам червяка и концентрация нагрузки значительно уменьшается, поэтому в расчетах принимают Кк=1.
2. Червячная передача работает плавно и бесшумно, поэтому значения Кд принимают меньше, чем зубчатой передачи. При V2≤3 м/с Кд=1…1,1 при V2>3 м/с Кд=1,1…1,2.
Планетарные и дифференциальные механизмы
Зубчатые передачи, имеющие колеса-сателлиты – обкатывающиеся вокруг центральных колес и, следовательно, имеющие подвижные оси, называются эпициклическими. Эти передачи делятся на планетарные, имеющие одно ведущее звено, и дифференциальные, имеющие два ведущих звена.
Планетарные механизмы. В зависимости от схемы планетарные механизмы могут осуществлять передаточные отношения от 3 до 1000 при к.п.д. от 0,98 до 0,01 соответственно. Ведущий и рабочий (выходной) валы расположены соосно. Размеры и массы – меньше, чем у зубчатых редукторов с неподвижными осями валов.
Схемы планетарных передач

Планетарный механизм состоит из неподвижного центрального колеса z3, жестко связанного с корпусом, подвижного центрального колеса z1, сателлита с колесами z2 и z2’ и водила H, на котором закреплена подвижная ось сателлита. Сателлит вращается относительно свой оси и одновременно обкатывается вокруг колеса z1. Зубья колеса z1 напоминают зубья колеса z2 сателлита и поворачивают его относительно неподвижного центрального колеса z3, при этом сателлит нажимает на ось водила и заставляет водило Н вращаться. Ведущий валик колеса z1 и ведомый валик водила Н расположены соосно.
Планетарные механизмы обычно имеют размеры и вес меньше, чем соответствующие им по силовым и кинематическим параметрам передачи с неподвижными осями колес. Это объясняется тем, что, применяя два или три сателлита, можно соответственно уменьшить нагрузку на зубья колес и использовать колеса с меньшими модулями и диаметрами.
Передаточное отношение планетарного механизма определяем методом обращения движения. Условно всем звеньям механизма сообщаем дополнительное движение с угловой скоростью водила wн, но в сторону, противоположную вращению последнего. То угловые скорости:
Водила Н: wн-wн=0
Колеса 1: w1-wн
Колеса 3: w3-wн
Сателлита 2: w2-wн
И любого колеса k механизма: wk-wn.
Планетарный механизм предотвращается в механизм с неподвижными осями валов. Передаточное отношение преобразованного механизма wk-wн.
Планетарный механизм превращается в механизм с неподвижными осями валов. Передаточное отношение преобразованного механизма от колеса 1 к колесу 3 при неподвижном водиле H: 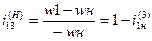
Верхний индекс при i в круглых скобках обозначает неподвижное звено механизма. В нижнем индексе первая цифра обозначает валик ведущего, а вторая валик ведомого (выходного) звена.
Из уравнения находим формулу для определения передаточного отношения планетарного механизма от колеса 1 к водилу H при неподвижном опорном колесе 3 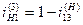
Передаточное отношение от водила Н к колесу 1 находим, как обратное передаточное отношение 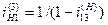 .
.
Выбор схемы планетарного механизма производится с учетом рациональных значений передаточного отношения и к.п.д.
Основными характеристиками планетарных механизмов являются:
-передаточное отношение от входного (воздушного) валика к выходному.
-к.п.д. механизма с подшипниками качения 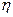 .
.
-модуль m.
-числа зубьев колес z1,z2,z1’ и z3.
-диаметры колес d1,d2,d2’ и d3.
-число сателлитов К.
-условие соосности валиков.
-условие сборки 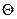 , обеспечивающее равенство центральных углов
, обеспечивающее равенство центральных углов 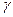 между сателлитами (
между сателлитами ( 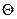 -целое число).
-целое число).
- условие соседства при к>3, обеспечивающее расположение нескольких сателлитов по окружности без соприкосновения их между собой.
Рассмотри схему 1. Рациональные передаточные отношения i1н=2,8…8, к.п.д.=0,98…0,96.
Так как 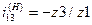 , то передаточное отношение механизма
, то передаточное отношение механизма
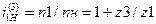
Условие соосности: z3-z1=2*z2
Условие сборки: (z3+z1)/k= 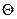 .
.
Числа зубьев колес подбирают путем совместного решения уравнений передаточного отношения и условия соосности с учетом условия сборки.
При больших передаточных отношениях для получения более высоких к.п.д. целесообразно применять схемы редукторов, составленных из нескольких последовательно соединенных схем 1.
Силовой расчет
При заданных 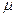 н или
н или 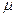 1, n1 (об/мин), i и
1, n1 (об/мин), i и 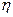 статические моменты
статические моменты 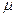 и мощности N на ведущих валах механизма определяем с учетом следующих зависимостей
и мощности N на ведущих валах механизма определяем с учетом следующих зависимостей
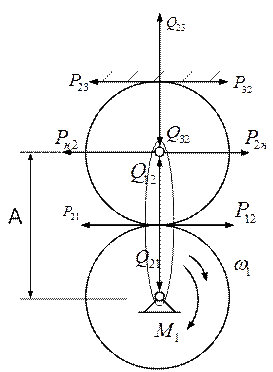
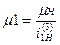
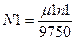
Силы, действующие на звенья механизма можно определить, рассматривая условия равновесия каждого звена. Определим приближенно (без учета к.п.д.) силы, действующие на звенья механизма:
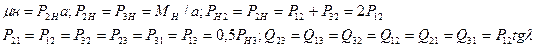
Эти силы учитывают при расчете колес, валов, и подшипников механизма.
Дифференциальные механизмы
Эти механизмы имеют две степени свободы и отличаются от планетарных тем, что у них вращается не одно, а оба центральных колеса z1 и z3. Они применяются в вычислительных устройствах, следящих системах автоматического управления, приборах и машинах, когда требуется осуществлять кинематическую связь между тремя валами.
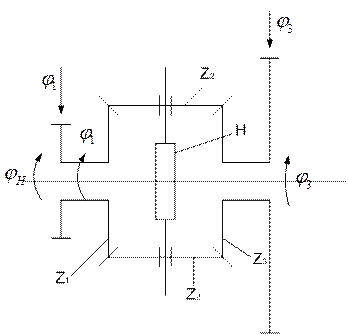
Передаточное отношение дифференциального механизма определяют рассмотренным выше методом обращения движения
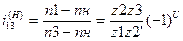 , где U – число внешних зубчатых зацеплений.
, где U – число внешних зубчатых зацеплений.
Пользуясь этой зависимостью при заданных числах оборотов в минуту n любых двух ведущих валов, можно определить число оборотов третьего ведомого вала. При n3=0 или n1=0 дифференциальный механизм превращается в планетарный.
Винтовые передачи(передача винт-гайка)
Винтовые механизмы используют для преобразования вращательного движения в прямолинейное поступательное.

Винтовой механизм состоит из винта 1, гайки 2 и стойки 3. в механизмах используется трапециидальная резьба β=15°, реже треугольная метрическая β=30°. Кинематика механизма определяется стандартными параметрами резьбы: d,d1 и d2 – наружным, внутренним и средним диаметрами; 2β – углом профиля резьбы; S – шагом, z – числом заходов, p=z*S – ходом винтовой линии, γ – углом подъема винтовой линии и ее направлением (правым или левым).
Известно, что tgγ=p/Пd2=zS/Пd2
Перемещение гайки L относительно стойки при повороте винта на угол α, определяется выражением
L=p*α1/360°
к.п.д. механизма: 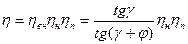
где φ=arctg(f/cosβ) – приведенный угол трения скольжения в резьбе, 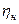 - к.п.д. направляющих гайки,
- к.п.д. направляющих гайки, 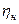 - к.п.д. подшипников винта. Ориентировочно принимают f: в зависимости от применяемых материалов,
- к.п.д. подшипников винта. Ориентировочно принимают f: в зависимости от применяемых материалов, 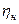 =0,95…0,85,
=0,95…0,85, 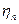 =0,96 для подшипников скольжения и
=0,96 для подшипников скольжения и 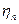 =0,99 для подшипников качения.
=0,99 для подшипников качения.
Расчет на прочность
Момент на винте 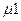 (Н*мм) при осевой силе T определяется по формуле
(Н*мм) при осевой силе T определяется по формуле 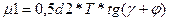
Винт рассчитывается из условия прочности на растяжение (или сжатие) с учетом кручения. Последнее учитывается коэффициентом к=1,25 для трапециидальной резьбы, к=1,35 для метрической резьбы. Коэффициент к равен отношению суммарного напряжения растяжения и кручения к напряжению растяжения.
Напряжения в материале винта (МПа)
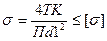
Винты резьбы рассчитываются из условия ограничения удельного давления между винтом и гайкой (МПа)
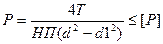 , где Н
, где Н 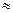 6 – расчетное число винтов гайки. [P] – допускаемое удельное давление между витками винта и гайки.
6 – расчетное число винтов гайки. [P] – допускаемое удельное давление между витками винта и гайки.
Гайки изготавливают из бронзы БрАЖ9-4, БрОФ10-1 или БрОЦС6-6-3, а винты из стали 40, 45, 50, 40Х или У10А. При этом принимают значения [P] для винтов и гаек 3 и 4 классов точности: для стали и бронзы 10…12 МПа. Для винтов 0, 1 и 2 классов точности [P] уменьшают в 2-3 раза.
Фрикционные передачи
Во фрикционных передачах движение от ведущего звена к ведомому передается за счет сил трения, возникающих между прижатыми друг к другу колесами. Различают фрикционные передачи с постоянным передаточным отношением и фрикционные вариаторы. Фрикционные передачи выполняются с жесткими рабочими материалами и с гибкой связью.
По характеру преобразования движения фрикционные передачи делятся: а)на передачи для преобразования вращающего движения ведущего звена во вращательное движение ведомого, при этом оси валов могут располагаться параллельно или пересекаться под углом, обычно 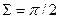 ; передачи для преобразования вращательного движения в винтовое и наоборот.
; передачи для преобразования вращательного движения в винтовое и наоборот.
Фрикционные передачи с бесступенчатым изменением передаточного отношения называются вариаторами. В вариаторах главное регулирование передаточного отношения осуществляется на ходу изменением рабочих радиусов ведущего R1 или ведомого R2 звеньев или обоих радиусов R1 и R2.
Прижатие рабочих тел друг к другу осуществляется обычно посредством специальных пружин, начальной затяжкой системы при сборке, собственной массой или грузом, а при кратковременной работе – вручную.
Фрикционные вариаторы широко используются в механизмах различных приборов, в счетно-решающих устройствах, испытательных стендах и машинах различного назначения. Они имеют диапазоны регулирования D=w2max/w2min=4…9.
К достоинствам фрикционных передач и вариаторов относятся: простота конструкции, плавность и бесшумность работы при высоких скоростях, проскальзывание при перегрузках, предотвращающее поломку механизма, отсутствие мертвого хода, возможность бесступенчатого регулирования скорости ведомого вала, возможность для выполнения математических операций в счетно-решающих устройствах.
К недостаткам фрикционных передач относятся: большое давление на валы и их опоры, проскальзывание при колебаниях нагрузки, нарушающее постоянство передаточного отношения, сравнительно быстрый и неравномерный износ деталей, большие габариты и большая масса при передаче больших крутящих моментов с малой скоростью.
Для уменьшения габаритов и сил прижатия фрикционные передачи и вариаторы рекомендуется располагать в механизмах приборов и машин ближе к двигателю на быстроходных валах, т.е. там, где больше скорости и меньше крутящие моменты.
В быстроходных передачах для уменьшения износа и нагрева металлических рабочих тел применяется смазка. При этом коэффициент трения f уменьшается и необходимая сила прижатия Q должна быть увеличена.
В передачах, работающих без смазки, рабочие поверхности колес(катков) защищаются от попадания на них смазки. Фрикционные передачи применяются обычно для передачи небольшой мощности. Передаточные отношения фрикционных передач не превышают следующих значений: i<7 в обычных передачах, i<15 в передачах разгруженными валами и i<25 в ручных передачах приборов.
Расчет
В реальной передаче под действием упругих деформаций рабочих тел и колебаний нагрузки всегда имеется небольшое скольжение (упругое скольжение), вызывающее отставание ведомого вала. Для обеспечения заданного передаточного отношения при проектировании упругое скольжение учитывается коэффициентом.
a=1,002…1,03. В этом случае i12=w1/w2=n1/n2=aR2/R1.
Откуда R1=a*R2/i12 R2=R1*i12/a.
Необходимая сила притяжения колес S, нормальная к поверхности их контакта, определяется из условия работы передачи без проскальзывания (без буксования) в зависимости от наибольшей окружной силы P12max. При 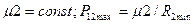 , а при
, а при 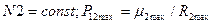 . Из условия F=f*S=cP12max находим S=c*P12max/f, где
. Из условия F=f*S=cP12max находим S=c*P12max/f, где 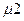 - вращающий момент на ведомом валике, R2 – радиус ведомого колеса при Pmax, мм; F-сила трения; f – коэффициент трения скольжения; с – коэффициент надежности работы передачи: для приборных механизмов с=2…3, а для силовых с=1,2…1,5.
- вращающий момент на ведомом валике, R2 – радиус ведомого колеса при Pmax, мм; F-сила трения; f – коэффициент трения скольжения; с – коэффициент надежности работы передачи: для приборных механизмов с=2…3, а для силовых с=1,2…1,5.
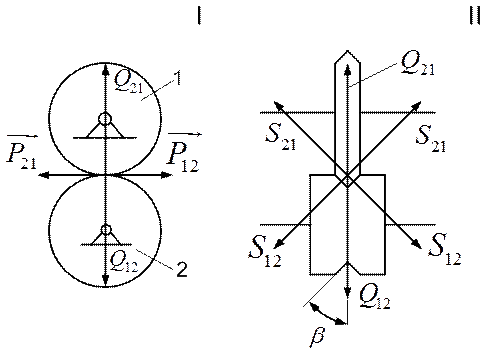
Силы, действующие в зоне контакта колес: окружные P, радиальные Q и осевые Т – являются составляющими силы Ы и определяются через окружную силу P12=P21 при S12=S21.
Для схемы I: Q12=S12, Q21=Q12;
Для схемы II: 2S12=cP12/f, Q12=2S12sinβ, Q21=Q12.
Прочность поверхностей контакта колес проверяется на основе формулы Герца. При контакте двух рабочих поверхностей по линии 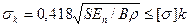 откуда ширина колеса
откуда ширина колеса 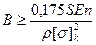 , где S – сила, нормальная к поверхностям контакта, Н; En=2E1*E2/(E1+E2) приведенный модуль упругости, МПа; E1 и E2 – модули упругости материалов колес 1 и 2;
, где S – сила, нормальная к поверхностям контакта, Н; En=2E1*E2/(E1+E2) приведенный модуль упругости, МПа; E1 и E2 – модули упругости материалов колес 1 и 2; 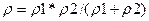 - приведенный радиус кривизны колес в зоне контакта; для двух цилиндрических колес
- приведенный радиус кривизны колес в зоне контакта; для двух цилиндрических колес 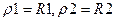 ; для конических колес
; для конических колес 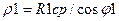 ,
, 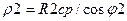 , где Rcp=0,5(Rmax+Rmin); при контакте по линии цилиндрической и плоской поверхностей принимают
, где Rcp=0,5(Rmax+Rmin); при контакте по линии цилиндрической и плоской поверхностей принимают 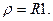
При контакте в точке, когда форма одной из рабочих поверхностей сферическая с радиусом кривизны образующей r:
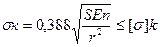 , где
, где 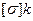 - допустимое контактное напряжения снятия, МПа, для материала менее прочной рабочей поверхности. Для закаленной стали
- допустимое контактное напряжения снятия, МПа, для материала менее прочной рабочей поверхности. Для закаленной стали 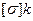 =800 МПа, для незакаленной стали
=800 МПа, для незакаленной стали 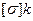 =500МПа, для текстолита ПТК при Е=6000МПа
=500МПа, для текстолита ПТК при Е=6000МПа 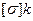 =110МПа, для чугуна
=110МПа, для чугуна 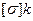 =1,5
=1,5 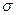 вМПА, где
вМПА, где 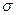 в – предел прочности при изгибе.
в – предел прочности при изгибе.
При чрезмерной перегрузке передачи возникает проскальзывание колес. При этом ведущее колесо вращается и изнашивается равномерно, а ведомое останавливается и изнашивается в одном месте. В связи с этим целесообразно рабочие поверхности ведомых колес изготавливать из более износостойкого материала.
Передачи гибкой связью
Передачи гибкой связью применяются для передачи вращения между валами при больших межосевых расстояниях и для преобразования вращательного движения в прямолинейное и наоборот. Передача состоит из ведущего и ведомого колес (роликов, шкивов, барабанов или звездочек) и охватывающей их гибкой связи.
Передачи гибкой связью могут иметь передаточные отношения: постоянные, переменные, ступенчато изменяющиеся и бесступенчато изменяющиеся.
По характеру сцепления гибкой связи с колесами передачи разделяются: на передачи с непосредственным соединением, передачи зацеплением; передачи трением.
В качестве гибкой связи применяются: а) шнуры шелковые, хлопчатобумажные, нейлоновые и кожаные; б) стальные канатики; в) стальные ленты; г)плоские ремни; д) клиновые ремни трапециидального сечения.
Передачи трением.
К ним относятся передачи шнуром, гибкой лентой и ременные передачи. Передача состоит из ведущего и ведомого шкивов(колес) и бесконечного шнура или ремня, надетого на них с предварительным натяжением. Передача усилия от одного шкива к другому осуществляется за счет сил трения между шнуром и ремнем и гладкими поверхностями шкивов.
15.10.14
Муфты. Классификация и назначение
Муфтами называются устройства, предназначенные для соединения валов с целью передачи вращения без изменения скорости. Необходимость в муфтах вызвана тем, что большинство механизмов приборных и вычислительных систем состоят из отдельных частей (блоков) c входными и выходными валами. Такими частями могут быть электродвигатель или рукоятка ручного привода, передаточный и исполнительный механизм, например, потенциометр, создающий определенную электрическую характеристику на входе. 1 – двигатель; 2 – муфты; 3 – передаточный механизм; 4 – исполнительный механизм.
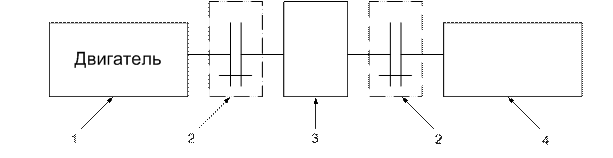
Здесь непосредственная кинематическая и силовая связь между частями аппарата или узла осуществляется с помощью муфт. Муфты, кроме непосредственного постоянного соединения валов могут использоваться для включения и выключения исполнительного механизма при работающем двигателе (сцепные муфты) или предохранять от перегрузки.
По назначению, конструкции и условиям работы муфты делятся на следующие типы: постоянные соединительные; сцепные управляемые, сцепные самоуправляющиеся (предохранительные, обгонные и центробежные).
Конструкции и основные параметры муфт, получивших широкое применение, регламентируются ГОСТами и ОСТами.
При выборе конструкции муфты необходимо учитывать ее назначение, особенности компоновки и сборки механизма , величину и характер действия нагрузки и условия эксплуатации.
1. Муфты постоянные соединительные. Постоянные соединительные муфты применяются в случаях, когда ведущий и ведомый валы должны быть соединены постоянно. Муфты делятся на две группы: глухие, жестко соединяющие валы, и подвижные, допускающие некоторую неточность сборки.
а). Глухие втулочные и дисковые муфты. Втулочная муфта состоит из втулки 1, соединенной с ведущими и ведомыми валами коническими штифтами 2 или шпонкой 3. Как правило, втулка одевается на валы с посадкой С(h6) или С3(h8). Ориентировочные размеры: D = 1,5d; l = (3…4)d;
dш = (0,3…0,25)d.
Втулку рассчитывают на кручение, а соединения штифтами или шпонками – на снятие и срез.
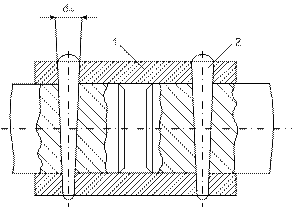
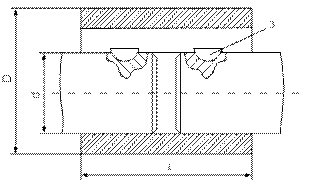
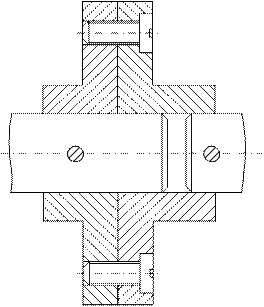
Дисковая муфта. Недостатком этих муфт является требование строгой соосности соединяемых валов. Смещение и перенос осей валов вызывает дополнительные деформации изгиба у валов и повышает давление на опоры.
б). Подвижные муфты.
В зависимости от конструкции эти муфты допускают некоторую неточность сборки валов.
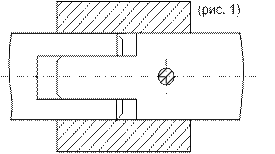
Расширительные муфты допускают небольшие осевые смещения валов, но требуют строгой их соосности. На рис 1) и 2) показаны расширительные муфты для передачи малых крутящих моментов Мк. Для передачи средних и больших моментов применяют кулачковые муфты (рис 2).
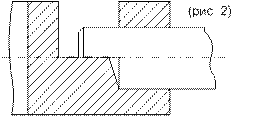
Боковые поверхности контакта кулачков рассчитываются на смятие
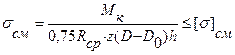
где Мк – крутящий момент;
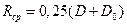 - средний радиус кулачков; z – число кулачков одной полумуфты; h – ширина рабочей поверхности кулачка; 0,75 – коэффициент; учитывающий неравномерность распределения нагрузки на кулачки вследствие не точности их изготовления.
- средний радиус кулачков; z – число кулачков одной полумуфты; h – ширина рабочей поверхности кулачка; 0,75 – коэффициент; учитывающий неравномерность распределения нагрузки на кулачки вследствие не точности их изготовления.

Поводковые муфты. Допускают небольшие смещения l < 0.8 мм параллельных валов. Конструкция этих муфт показана на рис 1). На диске или кривошипе 1 одной полумуфты закреплен палец 2, который входит со скользяще посадкой h6 – h8, h9 в радиальный паз второй полумуфты 3. Обычно диаметр пальца dп = 3, 4, 6 или 8 мм. Осевой зазор между дисками
б = 0,5…2 мм.
Наибольший мертвый ход в муфте в отсчетных единицах (о.е.)
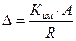 где А – цена оборота валика, о.е.; Ким – размерный коэффициент, мм
где А – цена оборота валика, о.е.; Ким – размерный коэффициент, мм
При dи = 3С Ким = 0,0022; при dи = 4С Ким = 0,0029
dи = 3C3 Ким = 0,0054; при dи = 4С3 Ким = 0,0068

К.П.Д. поводковой муфты приближенно применяют: при
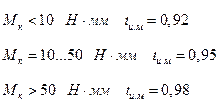
Ценой оборота Ак звена К называется число отсчетных единиц (о.е.) величины, которая воспроизводится на рабочем звене механизма, соответствующее одному полному обороту звеня К. Цены оборотов звеньев 1 и К связаны зависимостями: 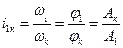
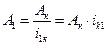 , где -
, где - 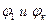 - углы поворота звеньев 1 и К.
- углы поворота звеньев 1 и К.
Крестовидная муфта с плавающим диском.
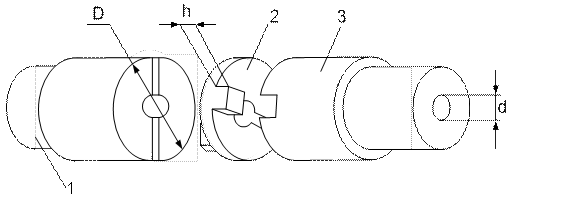
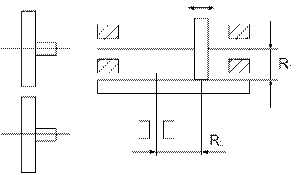
Состоит из двух полумуфт 1 и 3 с диаметрально расположенными пазами и промежуточного диска 2 с крестообразно расположенными выступами по одному на каждом торце. Такая муфта допускает смещение параллельных осей валов l < 0,5d и перенос осей валов a < 1°. Муфта с выступами в виде зуба эвольвентного профиля и диском, имеющем пазы трапециевидного сечения, допускает l £ 0,1d и a < 4°. При смещении l > 0 диск совершает плавающее круговое движение, не затрудняя вращение параллельных валов.
Рабочие поверхности выступов и пазов в деталях муфты рассчитываются на ограничение удельного давления
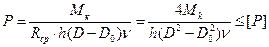 , где Мк – крутящий момент,
, где Мк – крутящий момент, 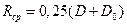 , h и
, h и 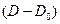 - средний радиус, ширина и длина рабочих поверхностей;
- средний радиус, ширина и длина рабочих поверхностей; 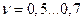 - коэффициент, учитывающий неравномерность распределения удельного давления вследствие неточности изготовления деталей; [P] – допускаемое удельное давление. Для стали по стали [P] ≤ 25 МПа; для стали по текстолиту [P] £ 10 МПа.
- коэффициент, учитывающий неравномерность распределения удельного давления вследствие неточности изготовления деталей; [P] – допускаемое удельное давление. Для стали по стали [P] ≤ 25 МПа; для стали по текстолиту [P] £ 10 МПа.
КПД крестовидной муфты приближенно применяют:
При:
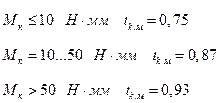
Наибольший мертвый ход (о.е) крестовидной муфты
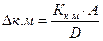 , где А – цена оборота валика, о.е.; D – наружный диаметр муфты;
, где А – цена оборота валика, о.е.; D – наружный диаметр муфты;
Кк.м – размерный коэффициент , мм. При d = 4 … 6 и посадке С Кк.м = 0,01 мм; при посадке 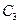
Кк.м = 0,024 мм.
Упругие муфты. Допускают небольшие смещения (l £ 1 мм) Эти муфты смягчают толчки от нагрузки и от инерционных сил и обладают хорошим демпирующими качествами. На (рис 1) изображена упругая пальцевая муфта с промежуточным диском из упругого материала – резины, кожи или фибры. Пальцы таких муфт проверяются на изгиб, а упругие элементы на смятие. При числе пальцев Z и силе на один палец
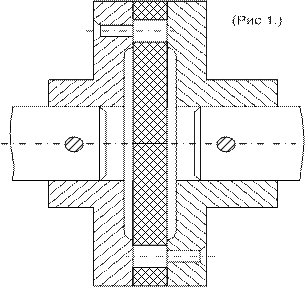
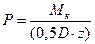
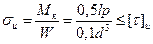
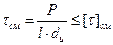
Материал полумуфт – сталь 35, пальцев – сталь 45 с 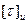 = 70…90 МПа, дисков – резина с
= 70…90 МПа, дисков – резина с 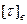 = 6 МПа и
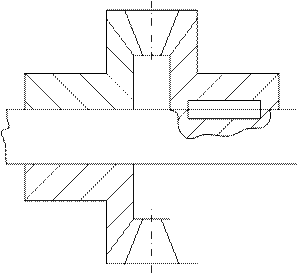
= 6 МПа и 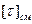 = 16 …20 МПа
= 16 …20 МПа
При больших Мк применяются стандартные муфты упругие втулочно – пальцевые (рис 2). Они выбираются по нормали МН 2096 – 64.
в). Муфты сцепные управляемые. Применяются в механизмах для соединения и разъединения двух валов или для соединения вала с насаженной на него деталью. Они делятся на кулачковые и зубчатые, фрикционные электромагнитные.
Первые допускают соединение валов в покое и при малой частоте вращения (до 1 об/с), а вторые и третьи позволяют включение и выключение при любой скорости вращения валов. Кулачковые и зубчатые муфты обеспечивают местную кинематическую связь и сохраняют постоянное взаимное расположение валов, а фрикционные и электромагнитные этого не обеспечивают.
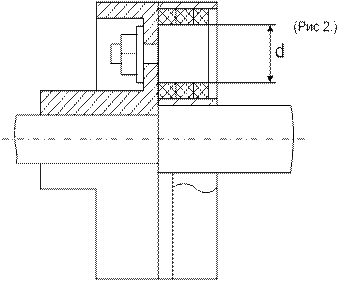
Кулачковые и зубчатые муфты. Эти муфты требуют точной соосности соединяемых. Зубчатая муфта состоит из одной полумуфты – шестерни с наружными зубьями 1 и второй полумуфты с внутренними зубьями 2 (зубья – эвольвентного профиля). Включается муфта осевым перемещением одной из полумуфт. Для удобства включения торцы зубьев у обеих полумуфт закругляются. Муфты имеют малые размеры, так как окружная сила распределяется на большое число зубьев. У кулачковых муфт выступы – кулачки, расположенные на торце одной полумуфты, при осевом перемещении входят во впадины между кулачками второй полумуфты.

В муфтах применяются различные профили кулачков.
Треугольный профиль а). обеспечивает легкость включения при числе зубьев z = 15…60, используется при малых Мк и требует большей силы прижатия полумуфт друг к другу, чем другие профили. Обычно β = 70°; t = ПD/z, h = t/2tgβ, tgg = 2h/D, в = (3…5)t
Трапецеидальный профиль б) применяется при больших Мк и w, b = 3…4° реже b = 5…10° z = 3…15. Сила прижатия полумуфт меньше, чем у треугольного профиля.
|


Прямоугольный профиль е). применяется в механизмах средней и большой мощности, нереверсивных при ручном включении. Этот профиль не обеспечивает без зазорного сцепления и не требует постоянной силы прижатия полумуфт.
Несимметричные профили в). Облегчают включение муфты в нереверсивных передачах.
Трапецеидальный с заострением профиль применяется для облегчения включения муфты.
В радиальном сечении муфты кулачки треугольного профиля имеют уменьшающуюся к центру муфты высоту h, так как шаг кулачков связан с радиусом муфты. Кулачки трапецеидального и прямоугольного профиля обычно имеют одинаковую высоту h по всей длине в. Боковые поверхности кулачков делаются плоскими.
Число кулачков Z тем больше, чем меньше требуемое время включения tв и крутящий момент Мк. Длина подвижной полумуфты в = (1,2…2,0)d, Rср = 0,5(D - d)
Кулачки рассчитываются на изгиб при неполном включении муфты и на ограничение удельного давления:


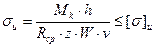
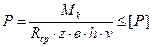
Где W – момент сопротивления площади сечения кулачка; v = 0,5…0,7 – коэффициент неравномерности распределения нагрузки на кулачки.
Кулачковые полумуфты обычно изготавливают из легированной стали 20х или 20хН2 с цементацией и закалкой кулачков до твердости HRC 54…60. При этом для муфт, включающихся в покое, принимают допускаемое удельное давление [P] = 80…120 МПа, а для включающихся при вращении [P] = 30…40 МПа. Допускаемые напряжения на изгиб 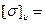 0,65
0,65 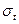 и
и 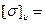 0,5
0,5 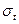 , где
, где 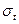 - предел текучести. 24.11.14
- предел текучести. 24.11.14
Фрикционные муфты. Эти муфты обеспечивают передачу крутящего момента от ведущего к ведомому валу за счет сил трения. Они допускают плавное включение и выключение при любой скорости вращения валов. По форме рабочих поверхностей муфты делятся: на дисковые с плоскими (торговыми) рабочими поверхностями, конусные и цилиндрические (колодочные и ленточные). По условиям смазки муфты делятся на сухие и смазываемые.
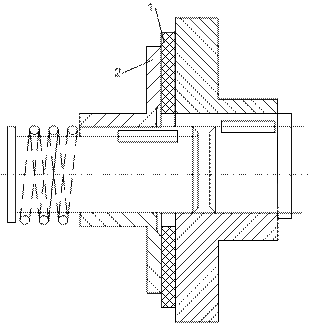
Сила прижатия дисков 1 и 2 друг к другу обеспечивается пружиной 3. Выключение муфты осуществляется перемещением диска 2 влево при одновременном сжатии пружины. Крутящий момент Мк, который может передавать фрикционная муфта, определяется из равенства:
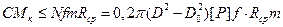 , где С = 1,25…1,5 – коэффициент запаса сцепления;
, где С = 1,25…1,5 – коэффициент запаса сцепления;
N – нормальная сила прижатия дисков; f – коэффициент трения между дисками; m – число поверхностей трения; [p] – допускаемое удельное давление; 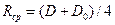 - средний радиус рабочих поверхностей дисков.
- средний радиус рабочих поверхностей дисков.
Условия нормальной работы: 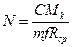
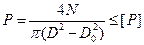
Конусная фрикционная муфта. Имеет коническую поверхность трения и обычно применяется для передачи небольших Мк. Для облегчения выключения муфты и предотвращения ее заклинивания угол a не должен быть меньше угла трения. Для металлических поверхностей трения примыкают a ³ 10…15°
Достоинством этой муфты является простота конструкции. К недостаткам следует отнести требование строгой соосности валов. Крутящий момент Мк, который может передавать муфта:
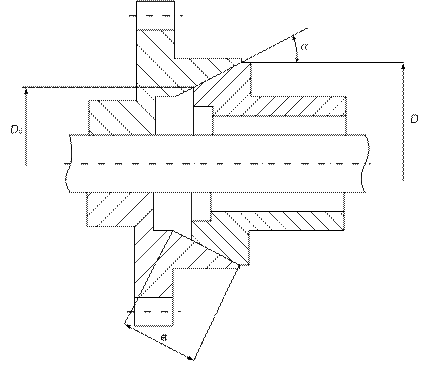
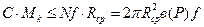
Задаваясь Rср, можно определить ширину поверхности трения в или, задаваясь отношением 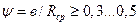 - значение Rср:
- значение Rср:

