В природных резервуарах
Цель и содержание.Научиться строить графическую модель разреза площади, с его термобарической характеристикой на основе данных, полученных при бурении структурной скважины (интервалы глубин залегания стратиграфических подразделений, замеренная температура, литологическая характеристика), а также опубликованным данным, характеризующим значения теплопроводности пород, коэффициента уравнений связи между соседними мощностями и коэффициента аномальности по разрезу.
В работе приведена методика расчета температурных параметров и параметров пластовых давлений.
Теоретическое обоснование. Знание величин ожидаемого пластового давления и температуры важно для научно-обоснованного проектирования поисков, разведки и разработки нефтяных и газовых месторождений.
Величина пластового давления определяется в основном геостатическим (горным) и гидростатическим давлениями, обусловленными соответственно весом вышележащих отложений и столбом жидкости заполняющей природный резервуар. Системы подземных вод, характеризующиеся общими условиями возникновения напора и движения вод называют геогидродинамическими системами. Они могут быть инфильтрационными (напор возникает вследствие инфильтрации поверхностных вод в коллекторы) и элизионными (напор создается за счет выжимания вод из уплотняющихся осадков).
Пластовое давление в инфильтрационных системах определяется по формуле:
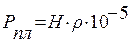, МПа, (7.1)
где Н – пьезометрический напор подземных вод (глубина залегания пласта-коллектора), м;
ρ – плотность воды, кг/м3; (принимается равной 1050 кг/м3 до 1000 м и 1100 кг/м3 для глубины более 1100 м).
В элизионных системах пластовое давление складывается из нормального гидростатического давления и приращения давления за счет избыточного поступления воды из уплотняющихся пород:
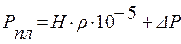, МПа. (7.2)
Возникает сверхгидростатическое пластовое давление (СГПД), часто неудачно называемое аномально высоким пластовым давлением (АВПД).
Вертикальный градиент СГПД превышает максимальный градиент нормального гидростатического давления равного 0,013 МПа на 1м глубины, и составляет 0,017 - 0,02 МПа на 1м мощности пород по разрезу.
Приращение давления в элизионных системах определяют по формуле:
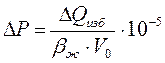, МПа, (7.3)
где ∆Qизб – превышение количества поступающей в пласт-коллектор воды, над количеством воды, удаляющейся из пласта в зоне разгрузки, м3;
β – коэффициент сжимаемости жидкости, м2/кг;
Vо – общий объем жидкости в системе, м3.
Отношение сверхгидростатического давления (Рпл.СГПД) к нормальному гидростатическому (Рпл н) называется коэффициентом аномальности (Ка), который изменяется в проделах 1,3 – 2,3.
Из многочисленных факторов, влияющих на возникновение СГПД, наиболее существенным является уплотнение пород.
Динамика уплотнения глинистых отложений и изменения пористости, и в конечном, счете давлений, математически проанализированы, опубликованы соответствующие графики и палетки. По палеткам определяется коэффициент аномальности давления, в реальной покрышке над резервуаром. Пластовое давление в нижележащем коллекторе принимается равным поровому в покрышке.
На сравнительно небольших глубинах пластовое давление рассчитывается как гидростатическое. Начиная с глубины 1000 метров, необходимо пользоваться коэффициентом аномальности, значения которого приведены в таблице 7.2. Расчет необходимо вести для подошвы каждого стратиграфического подразделения по формуле:
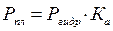, МПа (7.4)
Температура недр зависит главным образом, от внутреннего тепла Земли. Сезонные колебания охватывают лишь верхние 10 – 30 м пород и не прослеживаются глубже нейтрального слоя с постоянной температурой. Ниже него температура постоянно увеличивается.
Температуру в недрах оценивают по известному геотермическому градиенту (увеличение температуры на 100 метров). Обычно для осадочных горных пород геотермический градиент изменяется в пределах 2 – 8°С на 100 м глубины.
Для прогноза температуры в неразведанных горизонтах используют величину плотности теплового потока. Она связана с геотермическим градиентом следующим соотношением:
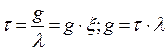, (7.5)
где τ – геотермический градиент;
g – плотность теплового потока, мВт/м2;
λ – теплопроводность пород, Вт/м°С;
ξ – тепловое сопротивление.
Поскольку величина теплового потока считается относительно устойчивой для отдельных регионов, то она может быть использована для прогноза температур глубоко залегающих горизонтов:
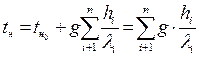, (7.6)
где tн – определяемая пластовая температура,°С;
tно – температура, замеренная на глубине Но, °С (из таблицы 7.2),
hi – толщина слоя однородного литологического состава, м.
Пусть имеется литологическая колонка площади (рисунок 7.1). Расчет необходимо начать с определения геотермического градиента по формуле:
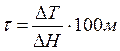, °С/100 м, (7.7)
где ΔT – приращение температуры от нейтрального слоя, залегающего на глубине 24 м, с постоянной температурой 16°C до замеренного значения tно;
ΔН – разность глубин от нейтрального слоя до глубины замера.
Затем из выражения (7.5) определяем величину плотности теплового потока, значения которой могут изменяться от 31 до 113 мВт/м2.
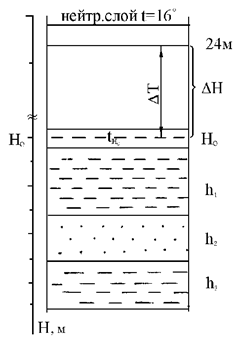
Рисунок 7.1 – Схематический литологический разрез
При этом следует использовать среднее значение теплопроводности пород, залегающих выше точки Но. Определим приращение температуры Δt в интервале пачки h1, залегающие непосредственно ниже точки hо:
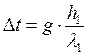, °С, (7.8)
где h1 – мощность пачки, м,
λ1 – теплопроводность глинистых пород. Вт/м°С.
Плотность теплового потока (g) для пород Предкавказья принята равной 50 мВт/м2.
Тогда температура в подошве h1 будет равна:
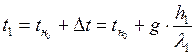, °С. (7.9)
Аналогично вычисляем значения температур в подошве всех литологических пачек разреза.
Значение теплопроводности пород (λ) для районов Предкавказья приведены в таблице 7.1, сведения о разрезе, вскрытом структурной скважиной, в таблице 7.2 (в 20 вариантах), литологическая характеристика вскрытых стратиграфических подразделений в таблице 7.3.
Таблица 7.1 – Значение теплопроводности пород (λ) для районов
Дата добавления: 2014-12-29; просмотров: 1286;