Процессы диффузии и осмоса, их роль в клеточных мембранах

Л. Больцман стремился дать интерпретацию термодинамики в рамках атомистической концепции с помощью статистической механики. Его идеи обрели реальность и значимость, когда было доказано, что материя состоит из атомов. Формулу Больцмана для энтропии проверили экспериментально, а статистический метод обрел предсказательную силу. Больцман считал, что с течением времени система побывает во всех энергетически возможных конфигурациях, т.е. будет возвращаться снова и снова к любой такой конфигурации. После его смерти эта идея вечного возврата была сформулирована в эргодическую гипотезу. Смысл ее в следующем. Состояние системы в классической физике изображается точкой в фазовом пространстве, поэтому при движении в фазовом пространстве точка проведет в каждой его области долю времени,

пропорциональную объему этой области. В квантовой механике объему фазового пространства соответствует число состояний. Исходя из эргодической гипотезы можно понять возникновение необратимых процессов.

В качестве примера рассмотрим процесс смешивания двух равных объемов воды при разных температурах. В результате процесса мы не получим отдельных слоев (горячего и холодного) в одном сосуде, т.е. энтропия полученной теплой воды окажется больше, чем сумма энтропии объемов воды до смешивания в соответствии со вторым началом термодинамики. Это означает, что и количество состояний при смешивании увеличилось. С позиции эргодической гипотезы точка проведет большую часть времени в области фазового пространства, соответствующей теплой воде, а в областях, соответствующих горячему и холодному слоям, — малое время. Опыт показывает, что возврата к отдельным слоям после смешивания можно ждать неограниченно долгое время. Введя необратимости, Больцман считал, что это соответствует тому, что исходное состояние очень невероятно, оно отвечает малому объему фазового пространства (или малой энтропии).

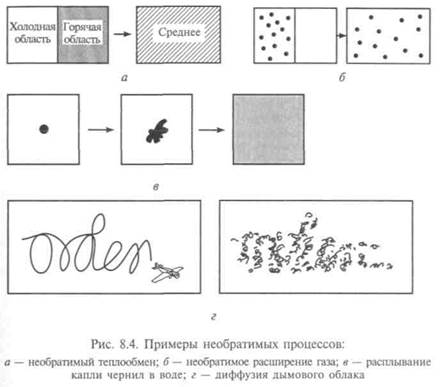
К необратимым процессам п е р е н о с а массы, энергии, импульса, заряда, количества движения и пр. относят явления, происходящие из-за перемешивания молекул. Такими процессами являются диффузия, термодиффузия, теплопроводность, вязкое течение, электропроводность, явления термоэлектричества, расширения газов в пустоту, осмос и др. (рис. 8.4). Из-за непрерывных столкновений друг с другом ни одна из молекул (или их групп) газа или жидкости не перемещается из одного участка сосуда в другой с большой скоростью. Если небольшой кристаллик йода поместить в сосуд с воздухом, то очень медленно начнут распространяться пары рыжего цвета. Этот процесс называется диффузией, т. е. пары йода диффундируют сквозь молекулы воздуха. Даже внешне процесс диффузии аналогичен процессу распространения теплоты в стержне, условием которого служит наличие градиента температуры. Для диффузии необходим градиент концентрации с, и его наличие позволяет рассчитать скорость изменения числа молекул в объеме dN/dt, которая пропорциональна площади поверхности S, через которую будет происходить диффузия.

Коэффициент диффузии D меняется в соответствии с уравнением dN/dt = -DS (dc/dx).

Это уравнение, похожее на уравнение распространения теплоты (знак минус показывает, что диффузия происходит противоположно росту концентрации), получил немецкий физиолог А.Фик (1855). В 1822 г. французский инженер Л. Навье математически описал движение вязкой жидкости. Через 100 лет выяснилось, что уравнения Фурье, Навье и Фика являются частными случаями общего уравнения, описывающего неравновесные процессы.

Скорость диффузии зависит от скоростей диффундирующих молекул с учетом коэффициента диффузии D. В кинетической теории среднеквадратичная скорость молекул пропорциональна Т/т, поэтому можно ожидать, что и коэффициент D будет также зависеть от температуры и массы. Опыты подтвердили это с высокой точностью. Можно проверить зависимость D от т по данным для некоторых небольших молекул в воздухе при атмосферном давлении: для водорода при T= О D = 6,34; для воды при Т= 8 D = 2,39; для кислорода при T= О D= 1,78; для углекислого газа при Т= 0 D = 1,39; для дисульфида углерода при Т= 20 D = = 1,02 (здесь T—°C, D — 0,00001 м²/с).

Диффузия в растворах, особенно в воде, важна для биосистем. Здесь также подходит закон Фика, но коэффициент диффузии 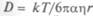, и из-за того, что масса m пропорциональна 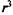, , 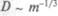в жидкостях коэффициент диффузии сильно зависит от массы частиц.

Используя связь коэффициентов диффузии отдельных молекул в воде и измеряя их, можно найти размеры молекул. Так как плотность р многих больших биологических молекул в сухом виде примерно равна 1,27 г/см³, а при погружении в воду к их поверх-

ности налипают молекулы воды, увеличивая их эффективный объем, то масса увеличивается почти в 1,5 раза. С учетом этого можно найти массы молекул по их размерам и средней плотности: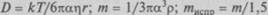

Диффузия молекулярных ионов через мембраны, образующие клеточные стенки, осуществляется при наличии определенного электрического потенциала внутри клетки. Кроме того, определенные химические процессы, происходящие внутри мембраны, меняют направление скорости диффузии различных ионов так, что по нервным волокнам распространяются электрические сигналы, представляющие нервный импульс. В биофизике распространен термин — транспорт частиц, являющийся синонимом диффузии. Процесс диффузии ответствен за 98 % необходимого кислорода, поглощаемого легкими. Стенки небольших емкостей внутри легких (альвеол), в которых происходит диффузия, имеют у взрослого человека площадь порядка 70 м², а толщину всего 0,5 мкм. Эти стенки плотно обвиты капиллярами, поэтому кровь циркулирует через мембраны легких только тоненькими струйками, причем ее общее количество около 100 мл. Так как площадь поверхности, через которую кислород диффундирует в кровь, а углекислый газ — обратно, очень велика, а толщина мембран мала, становится понятна эффективность процесса диффузии.

Диффузия через полупроницаемую перегородку названа осмосом. Мембрана полупроницаема, если она пористая и через нее возможна избирательная диффузия. Биологические мембраны часто проницаемы для воды, но непроницаемы для других веществ, растворенных в воде. Например, молекулы воды, имеющие диаметр 0,38 нм, проходят сквозь поры, а молекулы глюкозы диаметром 0,88 нм задерживаются. Но молекулы глюкозы не позволяют молекулам воды свободно подходить к мембране, замедляя скорость ее прохождения. Возникает разное осмотическое давление по разные стороны мембраны, а общее давление раствора равно сумме парциальных давлений разных составляющих. В 1887 г. Я. Вант-Гофф установил, что осмотическое давление пропорционально концентрации растворенного вещества с_в и температуре Т. Осмотическое давление раствора зависит от концентрации частиц, которые не могут пройти через мембрану, при этом ионизированные вещества создают большее давление, чем неионизирован-ные. Например, если при растворении в воде поваренной соли происходит разделение на две осмотические частицы, принято считать, что 1 моль NaCl соответствует 2 осмолям. Осмолярность, равная 1, отвечает 1 осмолю растворенного вещества в 1 л воды. Нормальная осмолярность клеточной жидкости 300 осмоль/м³, поэтому при нормальной температуре тела (Т = 310 К) осмотическое давление равно 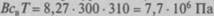. Получи-

лось огромное значение давления, и оно останется таким, если вокруг клетки будет чистая вода. На самом деле это не так: окружение имеет концентрацию, близкую к той, что внутри клетки, и если поместить клетку в чистую воду, разность осмотических давлений будет столь высока, что вода с большим напором устремится внутрь клетки и разорвет ее.

Осмос не обязательно связан с наличием мембран. Набухание — тоже осмотический эффект.