Пример. 1. Определение знака частного.
[А]пр = 0,101001;
[В]пр = 0,110011;
С = А/В.
1. Определение знака частного.
ЗнС = ЗнА Å ЗнВ = 0 Å 0 = 0.
2. Деление мантисс.
Частное Делитель
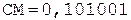


 0.
0. 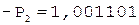
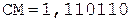 < 0, деление без переполнения
< 0, деление без переполнения
1. 


2. 
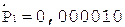



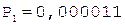
3. 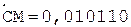
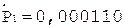
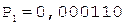
4. 


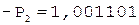
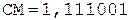

5. 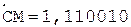
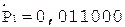
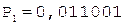
6. 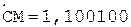

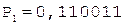
Таким образом, частное C = 0,110011.
Описанный метод позволяет ускорить выполнение операции деления только в тех циклах, в которых остаток денормализован, а в остальных циклах деление происходит по неускоренному алгоритму. Поэтому в худшем случае, при постоянном формировании нормализованного остатка, этот метод не дает прироста производительности.
Рассмотрим еще один метод ускорения выполнения операции деления, основанный на анализе двух разрядов очередного частичного остатка, при котором арифметическая операция может быть пропущена, если абсолютное значение удвоенного частичного остатка меньше делителя. В противном случае требуется выполнение арифметической операции, определяемой знаком сумматора. Поскольку в результате удвоения очередного частичного остатка может произойти переполнение сумматора, необходимо использовать модифицированный код. При переполнении сумматора содержащееся в нем число по модулю больше единицы, т.е. заведомо больше делителя, поэтому также следует выполнять арифметическую операцию, определяемую старшим знаковым разрядом сумматора.
В табл. 2.5 приведены различные сочетания пар старших разрядов регистра делителя и сумматора.
Таблица 2.5
| Старшие разряды сумматора | Старшие разряды модуля делителя | |
| 0,10 | 0,11 | |
| 0,00 1,11 | Арифм. операция не выполняется | Арифм. операция не выполняется |
| 0,01 1,10 | Арифм. операция не выполняется | Арифм. операция не выполняется |
| 0,10 1,01 | Требуется арифм. операция | Арифм. операция не выполняется |
| 0,11 1,00 | Требуется арифм. операция | Требуется арифм. операция |
Дата добавления: 2014-12-27; просмотров: 705;
